【数字图像处理4】小波变换 处理图像
文章目录
-
- 一、前言
-
- 实验目的
- 简单回顾一下小波变换:
- 二、环境配置
- 三、实验思路及过程(附图)
- 四、源代码
- 五、参考资料
一、前言
实验目的
用小波变换对图像去噪。
简单回顾一下小波变换:
数学公式我就不上了,估计上了也没人会认真看…
小波变换之所以诞生,是由于之前使用的傅里叶变换有一些缺点:
- 傅立叶变换提取信号的频谱,需要利用信号的全部时域信息。
- 傅立叶变换,没有随着时间的变化信号频率成分的变化情况。
- 傅立叶变换积分作用平滑了非平稳信号的突变成分。
用大白话说就是:
- 前两点:因为傅里叶变换是统计一段时间内的图像频率变化(高频低频波普啊什么的),他本身是不具备时间属性的,用户只知道这一段时间里面频域率总共发生了什么,但是先后顺序啊这种时间信息一概不知。
- 第三点:傅里叶变换由于本身性质,对于偶然出现的一个超大值点,会被其影响整个时间段的频率图像分布,但是小波变换由于具有时间属性,就能够锁定这个突变点(再进行什么操作那是后话,反正是知道这个突变点是什么时候出现的)
傅里叶变换:
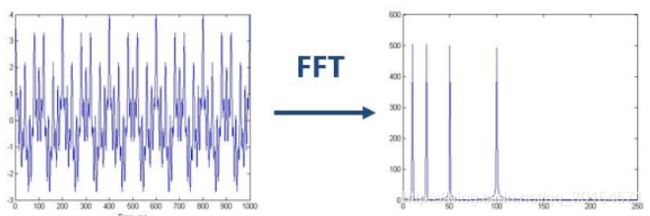
但是在这种情况,如图所示,傅里叶变换不能区分这两种图像区别:
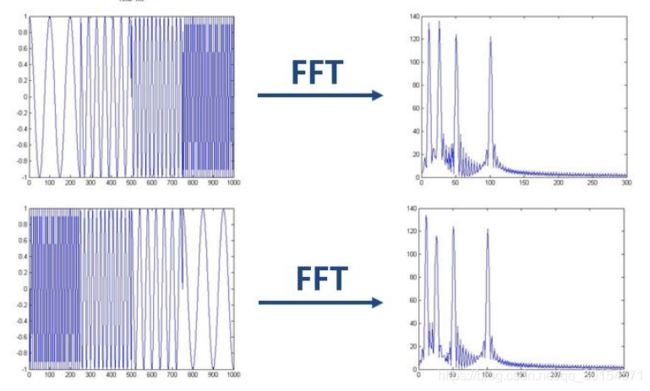
自然界的大量信号几乎都是非平稳的,所以在比如生物医学信号分析等领域的论文中,基本看不到单纯傅里叶变换这样naive的方法。所以就引出了小波变换:
- 首先,顾名思义,小波变换是对波进行了一些处理,把大波变成了小波的操作将无限长的三角函数基换成了有限长的会衰减的小波基。
- 这就是为什么它叫“小波”,因为是很小的一个波嘛~

- 小波还有一些好处,比如,我们知道对于突变信号,傅里叶变换存在吉布斯效应,我们用无限长的三角函数怎么也拟合不好突变信号:
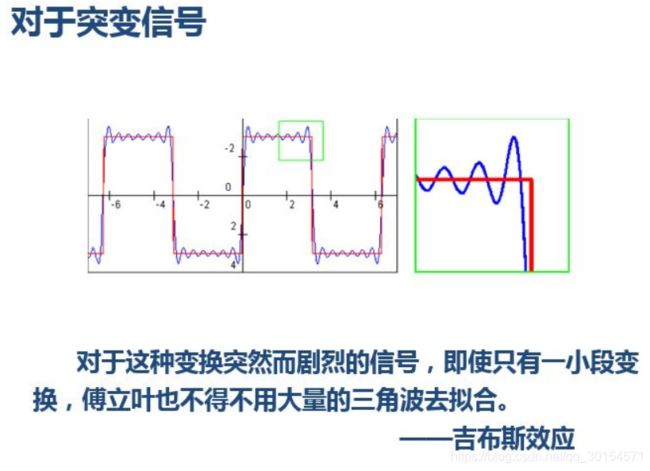
二、环境配置
python 小波库PyWavelets 直接在cmd中输入:
pip install PyWavelets
要运行PyWavelets所有测试还需要安装 Matplotlib 包
pip install Matplotlib.
三、实验思路及过程(附图)
- 首先,用小波变换(随便选去一个小波基,我用的哈尔)对图像进行分解,得到高低频分量(其中高频有三个分量)。
#读取灰度图
img = cv2.imread('pic/house.jpg',0)
#cA,cH,cV,cD 分别为近似分量(低频分量)、水平细节分量、垂直细节分量和对角细节分量
cA,(cH,cV,cD)=dwt2(img,'haar')#dwt2函数第二个参数指定小波基
#打印语句
plt.subplot(232), plt.imshow(cA, 'gray'), plt.title('cA')
plt.subplot(233), plt.imshow(cH, 'gray'), plt.title('cH')
plt.subplot(234), plt.imshow(cV, 'gray'), plt.title('cV')
plt.subplot(235), plt.imshow(cD, 'gray'), plt.title('cD')
- 之后,由于噪声往往是高频信息,所以我打算先对高频分量设一个阈值,把过高的高频像素点置0(并不是灰度值置0,是频率值置0,因为经过小波变换之后,我实际测试,像素的值就不是0~255了,而是有正有负,绝对值越大频率越大,0是频率最低值),为此我写了一个函数用来专门去噪,之后再主函数中处理高频分量看看效果:
def tool_Denoising(inputGrayPic,value):
result = inputGrayPic
height = result.shape[0]
weight = result.shape[1]
for row in range(height):
for col in range(weight):
result[row, col]
if (abs(result[row, col]) > value):
print(abs(result[row, col]))
result[row, col] = 0#频率的数值0为低频
return result
VALUE = 60
#处理水平高频
cH = tool_Denoising(cH,VALUE)
#处理垂直高频
cV = tool_Denoising(cV,VALUE)
#处理对角线高频
cD = tool_Denoising(cD,VALUE)
#重构图像
rebuild = idwt2((cA,(cH,cV,cD)), 'haar')
能看出来,虽然通过修改高频分量,好像能重构的图片比原图强了一点点,但是效果很有限。而且可以发现大部分的噪声其实还是来自低频分量cA。(不知道是否能够得出结论,仅仅一次小波变换之后出来的低频分量并不完全是低频分量?)
可以看出,这次的2阶低频分量(我姑且先用2阶这个词)就有比较明显的低频特征了,我打算大幅度舍去第二次变幻的高频细节,之后重构图像,试试效果:
#第二次小波变换
cA2,(cH2,cV2,cD2)=dwt2(cA,'haar')#dwt2函数第二个参数指定小波基
VALUE2 = 10
#处理水平高频
cH2 = tool_Denoising(cH2,VALUE2)
#处理垂直高频
cV2 = tool_Denoising(cV2,VALUE2)
#处理对角线高频
cD2 = tool_Denoising(cD2,VALUE2)
rebuild2 = idwt2((cA2,(cH2,cV2,cD2)), 'haar')
rebuild = idwt2((rebuild2,(cH,cV,cD)), 'haar')
最终的输入输出对比,也算是一定程度上完成了去噪(虽然我觉得也很像模糊),但是图案发浅,高频信息舍去过多这个问题最终我也没有解决。
四、源代码
说在前面,本次使用的是python的pywt包,文档入口:
https://pywavelets.readthedocs.io/en/latest/ref/index.html
import cv2
import numpy as np
from pywt import dwt2, idwt2
import matplotlib.pyplot as plt#用于显示图片
##################################################################################
############################遍历图像,将高频点置0#################################
##################################################################################
def tool_Denoising(inputGrayPic,value):
result = inputGrayPic
height = result.shape[0]
weight = result.shape[1]
for row in range(height):
for col in range(weight):
result[row, col]
if (abs(result[row, col]) > value):
print(abs(result[row, col]))
result[row, col] = 0#频率的数值0为低频
return result
##################################################################################
##################################################################################
##################################################################################
#读取灰度图
img = cv2.imread('pic/house.jpg',0)
#cA,cH,cV,cD 分别为近似分量(低频分量)、水平细节分量、垂直细节分量和对角细节分量
cA,(cH,cV,cD)=dwt2(img,'haar')#dwt2函数第二个参数指定小波基
#打印语句
#plt.subplot(232), plt.imshow(cA, 'gray'), plt.title('cA')
#plt.subplot(233), plt.imshow(cH, 'gray'), plt.title('cH')
#plt.subplot(234), plt.imshow(cV, 'gray'), plt.title('cV')
#plt.subplot(235), plt.imshow(cD, 'gray'), plt.title('cD')
#设置去噪阈值。因为噪音一般都是高频信息,遍历像素,将VALUE的像素点置0
VALUE = 60
#处理低频
#cA = tool_Denoising(cA,100)
#处理水平高频
cH = tool_Denoising(cH,VALUE)
#处理垂直高频
cV = tool_Denoising(cV,VALUE)
#处理对角线高频
cD = tool_Denoising(cD,VALUE)
#重构图像
rebuild = idwt2((cA,(cH,cV,cD)), 'haar')
#第二次小波变换
cA2,(cH2,cV2,cD2)=dwt2(cA,'haar')#dwt2函数第二个参数指定小波基
VALUE2 = 10
#处理水平高频
cH2 = tool_Denoising(cH2,VALUE2)
#处理垂直高频
cV2 = tool_Denoising(cV2,VALUE2)
#处理对角线高频
cD2 = tool_Denoising(cD2,VALUE2)
rebuild2 = idwt2((cA2,(cH2,cV2,cD2)), 'haar')
rebuild = idwt2((rebuild2,(cH,cV,cD)), 'haar')
plt.subplot(231), plt.imshow(img, 'gray'), plt.title('img')
plt.subplot(232), plt.imshow(cA, 'gray'), plt.title('cA')
plt.subplot(233), plt.imshow(cH, 'gray'), plt.title('cH')
plt.subplot(234), plt.imshow(cV, 'gray'), plt.title('cV')
plt.subplot(235), plt.imshow(cD, 'gray'), plt.title('cD')
plt.subplot(236), plt.imshow(rebuild, 'gray'), plt.title('rebuild')
#打印图片
#plt.subplot(231), plt.imshow(img, 'gray'), plt.title('Input')
#plt.subplot(232), plt.imshow(cA2, 'gray'), plt.title('cA2')
#plt.subplot(233), plt.imshow(cH2, 'gray'), plt.title('cH2')
#plt.subplot(234), plt.imshow(cV2, 'gray'), plt.title('cV2')
#plt.subplot(235), plt.imshow(cD2, 'gray'), plt.title('cD2')
#plt.subplot(236), plt.imshow(rebuild, 'gray'), plt.title('rebuild')
plt.axis('off')
plt.show()
五、参考资料
单尺度二维离散小波重构(逆变换)idwt2
https://www.cnblogs.com/xixixing/p/5827599.html
【图像处理】python小波变换
https://blog.csdn.net/u011285477/article/details/104162355
形象易懂讲解算法I——小波变换
https://zhuanlan.zhihu.com/p/22450818





