Paddlepaddle(2.0-beta版本)-Tensor详解
简介
要学习框架,必须先去了解文档(血一般的教训),在此做下记录,方便后人。
飞桨文档
开始
Tensor概念介绍
飞桨(PaddlePaddle,以下简称Paddle)和其他深度学习框架一样,使用Tensor来表示数据,在神经网络中传递的数据均为Tensor。
Tensor可以将其理解为多维数组,其可以具有任意多的维度,不同Tensor可以有不同的数据类型 (dtype) 和形状 (shape)。
同一Tensor的中所有元素的dtype均相同。如果你对 Numpy 熟悉,Tensor是类似于 Numpy array 的概念。
目录
- Tensor的创建
- Tensor的shape
- Tensor其他属性
- Tensor的操作
Tensor的创建
首先,让我们开始创建一个 Tensor :
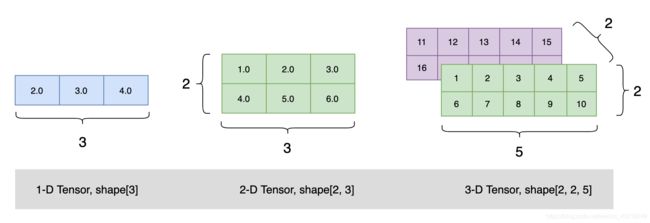
- 创建类似于vector的1-D Tensor,其rank为1
#可通过dtype来指定Tensor数据类型,否则会创建float32类型的Tensor
rank_1_tensor = paddle.to_tensor([2.0, 3.0, 4.0], dtype='float64')
print(rank_1_tensor)
Tensor: generated_tensor_1
- place: CUDAPlace(0)
- shape: [3]
- layout: NCHW
- dtype: double
- data: [2.0, 3.0, 4.0]
特殊地,如果仅输入单个scalar类型数据(例如float/int/bool类型的单个元素),则会创建shape为[1]的Tensor
paddle.to_tensor(2)
paddle.to_tensor([2])
上述两种创建方式完全一致,shape均为[1],输出如下:
Tensor: generated_tensor_0
- place: CUDAPlace(0)
- shape: [1]
- layout: NCHW
- dtype: int32_t
- data: [2]
- 创建类似于matrix的2-D Tensor,其rank为2
rank_2_tensor = paddle.to_tensor([[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0]])
print(rank_2_tensor)
Tensor: generated_tensor_2
- place: CUDAPlace(0)
- shape: [2, 3]
- layout: NCHW
- dtype: double
- data: [1.0 2.0 3.0 4.0 5.0 6.0]
- 同样地,还可以创建rank为3、4…N等更复杂的多维Tensor
# Tensor可以有任意数量的轴(也称为维度)
rank_3_tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
print(rank_3_tensor)
Tensor: generated_tensor_3
- place: CUDAPlace(0)
- shape: [2, 2, 5]
- layout: NCHW
- dtype: double
- data: [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20]
上述不同rank的Tensor可以可视化的表示为:
你可以通过 Tensor.numpy() 方法方便地将 Tensor 转化为 Numpy array:
print(rank_2_tensor.numpy())
array([[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0]], dtype=float32)
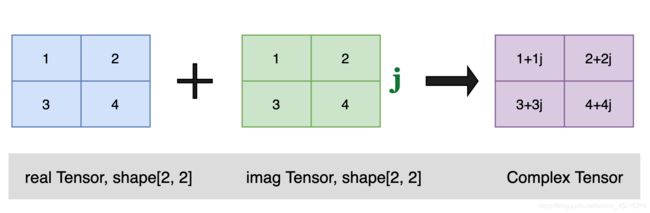
Tensor不仅支持 floats、ints 类型数据,也支持 complex numbers 数据:
rank_2_complex_tensor = paddle.to_tensor([[1+1j, 2+2j],
[3+3j, 4+4j]])
CompleTensor[real]: generated_tensor_0.real
- place: CUDAPlace(0)
- shape: [2, 2]
- layout: NCHW
- dtype: float
- data: [1 2 3 4]
CompleTensor[imag]: generated_tensor_0.real
- place: CUDAPlace(0)
- shape: [2, 2]
- layout: NCHW
- dtype: float
- data: [1 2 3 4]
如果检测到输入数据包含complex numbers,则会自动创建一个ComplexTensor,ComplexTensor是Paddle中一种特殊的数据结构, 其包含实部(real)与虚部(imag)两个形状与数据类型相同的Tensor,其结构可视化表示为:
Tensor必须形状规则,类似于“矩形”的概念,也就是,沿任何一个轴(也称作维度)上,元素的数量都是相等的,如果为以下情况:
rank_2_tensor = paddle.to_tensor([[1.0, 2.0],
[4.0, 5.0, 6.0]])
该情况下将会抛出异常:
ValueError:
Faild to convert input data to a regular ndarray :
- Usually this means the input data contains nested lists with different lengths.
上面介绍了通过Python数据来创建Tensor的方法,我们也可以通过 Numpy array 来创建Tensor:
rank_1_tensor = paddle.to_tensor(Numpy array([1.0, 2.0]))
rank_2_tensor = paddle.to_tensor(Numpy array([[1.0, 2.0],
[3.0, 4.0]]))
rank_3_tensor = paddle.to_tensor(numpy.random.rand(3, 2))
创建的 Tensor 与原 Numpy array 具有相同的 shape 与 dtype。
如果要创建一个指定shape的Tensor,Paddle也提供了一些API:
paddle.zeros([m, n]) # 创建数据全为0,shape为[m, n]的Tensor
paddle.ones([m, n]) # 创建数据全为1,shape为[m, n]的Tensor
paddle.full([m, n], 10) # 创建数据全为10,shape为[m, n]的Tensor
paddle.arrange(start, end, step) # 创建从start到end,步长为step的Tensor
paddle.linspace(start, end, num) # 创建从start到end,元素个数固定为num的Tensor
Tensor的shape
基本概念
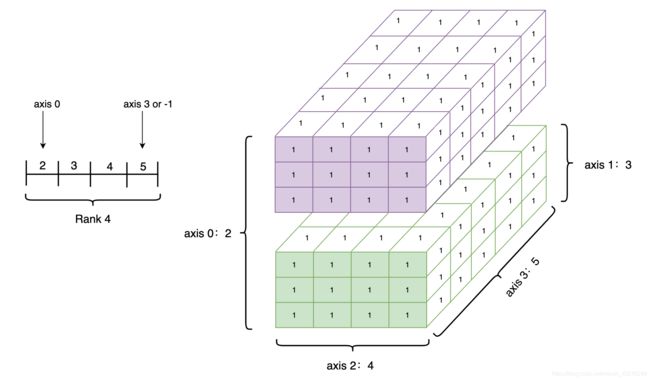
查看一个Tensor的形状可以通过 Tensor.shape,shape是 Tensor 的一个重要属性,以下为相关概念:
- shape:描述了tensor的每个维度上的元素数量
- rank: tensor的维度的数量,例如vector的rank为1,matrix的rank为2.
- axis或者dimension:指tensor某个特定的维度
- size:指tensor中全部元素的个数
让我们来创建1个4-D Tensor,并通过图形来直观表达以上几个概念之间的关系;
rank_4_tensor = paddle.ones([2, 3, 4, 5])
print("Data Type of every element:", rank_4_tensor.dtype)
print("Number of dimensions:", rank_4_tensor.ndim)
print("Shape of tensor:", rank_4_tensor.shape)
print("Elements number along axis 0 of tensor:", rank_4_tensor.shape[0])
print("Elements number along the last axis of tensor:", rank_4_tensor.shape[-1])
Data Type of every element: VarType.FP32
Number of dimensions: 4
Shape of tensor: [2, 3, 4, 5]
Elements number along axis 0 of tensor: 2
Elements number along the last axis of tensor: 5
索引
通过索引能方便地对Tensor进行“切片”操作。Paddle使用标准的 Python索引规则 与 Numpy索引规则,与ndexing a list or a string in Python类似。具有以下特点:
-
如果索引为负数,则从尾部开始计算
-
如果索引使用 : ,则其对应格式为start: stop: step,其中start、stop、step均可缺省
- 针对1-D Tensor,则仅有单个轴上的索引:
rank_1_tensor = paddle.to_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
print("Origin Tensor:", rank_1_tensor.numpy())
print("First element:", rank_1_tensor[0].numpy())
print("Last element:", rank_1_tensor[-1].numpy())
print("All element:", rank_1_tensor[:].numpy())
print("Before 3:", rank_1_tensor[:3].numpy())
print("From 6 to the end:", rank_1_tensor[6:].numpy())
print("From 3 to 6:", rank_1_tensor[3:6].numpy())
print("Interval of 3:", rank_1_tensor[::3].numpy())
print("Reverse:", rank_1_tensor[::-1].numpy())
Origin Tensor: array([0, 1, 2, 3, 4, 5, 6, 7, 8], dtype=int64)
First element: [0]
Last element: [8]
All element: [0 1 2 3 4 5 6 7 8]
Before 3: [0 1 2]
From 6 to the end: [6 7 8]
From 3 to 6: [3 4 5]
Interval of 3: [0 3 6]
Reverse: [8 7 6 5 4 3 2 1 0]
- 针对2-D及以上的 Tensor,则会有多个轴上的索引:
rank_2_tensor = paddle.to_tensor([[0, 1, 2, 3],
[4, 5, 6, 7],
[8, 9, 10, 11]])
print("Origin Tensor:", rank_2_tensor.numpy())
print("First row:", rank_2_tensor[0].numpy())
print("First row:", rank_2_tensor[0, :].numpy())
print("First column:", rank_2_tensor[:, 0].numpy())
print("Last column:", rank_2_tensor[:, -1].numpy())
print("All element:", rank_2_tensor[:].numpy())
print("First row and second column:", rank_2_tensor[0, 1].numpy())
Origin Tensor: array([[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]], dtype=int64)
First row: [0 1 2 3]
First row: [0 1 2 3]
First column: [0 4 8]
Last column: [ 3 7 11]
All element: [[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
First row and second column: [1]
输入索引的第一个值对应axis 0,第二个值对应axis 1,以此类推,如果某个axis上未指定索引,则默认为 : 。例如:
rank_3_tensor[1]
rank_3_tensor[1, :]
rank_3_tensor[1, :, :]
以上三种索引的结果是完全相同的。
对shape进行操作
重新定义Tensor的shape在实际编程中具有重要意义。
rank_3_tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]],
[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]]])
print("the shape of rank_3_tensor:", rank_3_tensor.shape)
the shape of rank_3_tensor: [3, 2, 5]
Paddle提供了reshape接口来改变Tensor的shape:
rank_3_tensor = paddle.reshape(rank_3_tensor, [2, 5, 3])
print("After reshape:", rank_3_tensor.shape)
After reshape: [2, 5, 3]
在指定新的shape时存在一些技巧:
- -1 表示这个维度的值是从Tensor的元素总数和剩余维度推断出来的。因此,有且只有一个维度可以被设置为-1。 2. 0 表示实际的维数是从Tensor的对应维数中复制出来的,因此shape中0的索引值不能超过x的维度。
有一些例子可以很好解释这些技巧:
origin:[3, 2, 5] reshape:[3, 10] actual: [3, 10]
origin:[3, 2, 5] reshape:[-1] actual: [30]
origin:[3, 2, 5] reshape:[0, 5, -1] actual: [3, 5, 2]
可以发现,reshape为[-1]时,会将tensor按其在计算机上的内存分布展平为1-D Tensor。
print("Tensor flattened to Vector:", paddle.reshape(rank_3_tensor, [-1]).numpy())
Tensor flattened to Vector: [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
Tensor其他属性
Tensor的dtype
Tensor的数据类型,可以通过 Tensor.dtype 来查看,dtype支持:‘bool’,‘float16’,‘float32’,‘float64’,‘uint8’,‘int8’,‘int16’,‘int32’,‘int64’。
- 通过Python元素创建的Tensor,可以通过dtype来进行指定,如果未指定:
-
对于python整型数据,则会创建int64型Tensor
-
对于python浮点型数据,默认会创建float32型Tensor,并且可以通过set_default_type来调整浮点型数据的默认类型。
- 通过Numpy array创建的Tensor,则与其原来的dtype保持相同。
print("Tensor dtype from Python integers:", paddle.to_tensor(1).dtype)
print("Tensor dtype from Python floating point:", paddle.to_tensor(1.0).dtype)
Tensor dtype from Python integers: VarType.INT64
Tensor dtype from Python floating point: VarType.FP32
Paddle提供了cast接口来改变dtype:
float32_tensor = paddle.to_tensor(1.0)
float64_tensor = paddle.cast(float32_tensor, dtype='float64')
print("Tensor after cast to float64:", float64_tensor.dtype)
int64_tensor = paddle.cast(float32_tensor, dtype='int64')
print("Tensor after cast to int64:", int64_tensor.dthpe)
Tensor after cast to float64: VarType.FP64
Tensor after cast to int64: VarType.INT64
Tensor的place
初始化Tensor时可以通过place来指定其分配的设备位置,可支持的设备位置有三种:CPU/GPU/固定内存,其中固定内存也称为不可分页内存或锁页内存,其与GPU之间具有更高的读写效率,并且支持异步传输,这对网络整体性能会有进一步提升,但其缺点是分配空间过多时可能会降低主机系统的性能,因为其减少了用于存储虚拟内存数据的可分页内存。
创建CPU上的Tensor:
cpu_tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
print(cpu_tensor)
Tensor: generated_tensor_0
- place: CPUPlace
创建GPU上的Tensor:
gpu_tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print(gpu_tensor)
Tensor: generated_tensor_0
- place: CUDAPlace(0)
创建固定内存上的Tensor:
pin_memory_tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print(pin_memory_tensor)
Tensor: generated_tensor_0
- place: CUDAPinnedPlace
Tensor的name
Tensor的name是其唯一的标识符,为python 字符串类型,查看一个Tensor的name可以通过Tensor.name属性。默认地,在每个Tensor创建时,Paddle会自定义一个独一无二的name。
print("Tensor name:", paddle.to_tensor(1).name)
Tensor name: generated_tensor_0
Tensor的操作
Paddle提供了丰富的Tensor操作的API,包括数学运算符、逻辑运算符、线性代数相关等100+余种API,这些API调用有两种方法:
x = paddle.to_tensor([[1.1, 2.2], [3.3, 4.4]])
y = paddle.to_tensor([[5.5, 6.6], [7.7, 8.8]])
print(paddle.add(x, y), "\n")
print(x.add(y), "\n")
Tensor: eager_tmp_2
- place: CUDAPlace(0)
- shape: [2, 2]
- layout: NCHW
- dtype: float
- data: [6.6 8.8 11 13.2]
Tensor: eager_tmp_3
- place: CUDAPlace(0)
- shape: [2, 2]
- layout: NCHW
- dtype: float
- data: [6.6 8.8 11 13.2]
可以看出,使用 Tensor类成员函数 和 paddle API 具有相同的效果,由于 类成员函数 操作更为方便,以下均从 Tensor类成员函数 的角度,对常用Tensor操作进行介绍。
数学运算符
x.abs() #绝对值
x.ceil() #向上取整
x.floor() #向下取整
x.exp() #逐元素计算自然常数为底的指数
x.log() #逐元素计算x的自然对数
x.reciprocal() #求倒数
x.square() #逐元素计算平方
x.sqrt() #逐元素计算平方根
x.sum() #计算所有元素的和
x.asin() #逐元素计算反正弦函数
x.add(y) #逐元素相加
x.add(-y) #逐元素相减
x.multiply(y) #逐元素相乘
x.divide(y) #逐元素相除
x.floor_divide(y) #逐元素相除并取整
x.remainder(y) #逐元素相除并取余
x.pow(y) #逐元素幂运算
x.reduce_max() #所有元素最大值,可以指定维度
x.reduce_min() #所有元素最小值,可以指定维度
x.reduce_prod() #所有元素累乘,可以指定维度
x.reduce_sum() #所有元素的和,可以指定维度
Paddle对python数学运算相关的魔法函数进行了重写,以下操作与上述结果相同。
x + y -> x.add(y) #逐元素相加
x - y -> x.add(-y) #逐元素相减
x * y -> x.multiply(y) #逐元素相乘
x / y -> x.divide(y) #逐元素相除
x // y -> x.floor_divide(y) #逐元素相除并取整
x % y -> x.remainder(y) #逐元素相除并取余
x ** y -> x.pow(y) #逐元素幂运算
逻辑运算符
x.is_empty() #判断tensor是否为空
x.isfinite() #判断tensor中元素是否是有限的数字,即不包括inf与nan
x.euqal_all(y) #判断两个tensor的所有元素是否相等
x.euqal(y) #判断两个tensor的每个元素是否相等
x.not_equal(y) #判断两个tensor的每个元素是否不相等
x.less_than(y) #判断tensor x的元素是否小于tensor y的对应元素
x.less_equal(y) #判断tensor x的元素是否小于或等于tensor y的对应元素
x.greater_than(y) #判断tensor x的元素是否大于tensor y的对应元素
x.greater_equal(y) #判断tensor x的元素是否大于或等于tensor y的对应元素
同样地,Paddle对python逻辑比较相关的魔法函数进行了重写,以下操作与上述结果相同。
x == y -> x.euqal(y) #判断两个tensor的每个元素是否相等
x != y -> x.not_equal(y) #判断两个tensor的每个元素是否不相等
x < y -> x.less_than(y) #判断tensor x的元素是否小于tensor y的对应元素
x <= y -> x.less_equal(y) #判断tensor x的元素是否小于或等于tensor y的对应元素
x > y -> x.greater_than(y) #判断tensor x的元素是否大于tensor y的对应元素
x >= y -> x.greater_equal(y) #判断tensor x的元素是否大于或等于tensor y的对应元素
以下操作仅针对bool型Tensor:
x.reduce_all() #判断一个bool型tensor是否所有元素为True
x.reduce_any() #判断一个bool型tensor是否存在至少1个元素为True
x.logical_and(y) #对两个bool型tensor逐元素进行逻辑与操作
x.logical_or(y) #对两个bool型tensor逐元素进行逻辑或操作
x.logical_xor(y) #对两个bool型tensor逐元素进行逻辑亦或操作
x.logical_not(y) #对两个bool型tensor逐元素进行逻辑非操作
线性代数相关
x.cholesky() #矩阵的cholesky分解
x.t() #矩阵转置
x.transpose([1, 0]) #交换axis 0 与axis 1的顺序
x.norm('pro') #矩阵的Frobenius 范数
x.dist(y, p=2) #矩阵(x-y)的2范数
x.matmul(y) #矩阵乘法
需要注意,Paddle中Tensor的操作符均为非inplace操作,即 x.add(y) 不会在tensor x上直接进行操作,而会返回一个新的Tensor来表示运算结果。