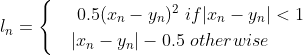深度学习损失函数numpy实现并与torch对比

用numpy实现L1损失、MSE损失、KL损失、NLL损失、交叉熵损失、BCE损失、SmoothL1损失，并和torch的计算结果对比。

目录

一、L1损失

1、公式

2、实现及对比

二、MSE损失

1、公式

2、实现及对比

三、 交叉熵损失

1、公式

2、实现及对比

四、NLL损失

1、公式

2、实现及对比

五、Kullback-Leibler divergence 损失

1、公式

​2、实现及对比

六、BCE损失

一、公式

2、实现及对比

七、SMOOTHL1损失

一、公式

2、实现及对比

---

若无特殊声明，文中表示预测值，表示目标值。

一、L1损失

1、公式

L1损失函数又被称为最小绝对值偏差（LAD），最小绝对值误差（LAE），它的公式如下：

2、实现及对比

import torch
import numpy as np


def l1_loss(x, y, reduction='mean'):
    dif = np.abs(x - y)
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)
    return dif


np.random.seed(10001)
x = np.random.rand(4, 3, 100)
y = np.random.rand(4, 3, 100)
np_loss = l1_loss(x, y, 'mean')
torch_loss_fn = torch.nn.L1Loss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y))
print(np_loss, torch_loss.numpy())
# 输出：0.3279294731209465 0.3279294731209465

二、MSE损失

1、公式

均方差损失是预测数据和原始数据对应点误差的平方和的均值，它的公式如下：

2、实现及对比

import torch
import numpy as np


def mse_loss(x, y, reduction='mean'):
    dif = np.square(x - y)
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)
    return dif


np.random.seed(10001)

x = np.random.rand(4, 3, 100)
y = np.random.rand(4, 3, 100)
np_loss = mse_loss(x, y, 'mean')
torch_loss_fn = torch.nn.MSELoss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y))
print(np_loss, torch_loss.numpy())
# 输出：0.16281742957744108 0.16281742957744105

三、 交叉熵损失

1、公式

交叉熵损失函数常用于解决分类问题，在构建深度学习模型是，为了数值计算稳定，一般将logits（sigmoid或者softmax的输入）送入损失函数计算损失。

  

2、实现及对比

import torch
import numpy as np


def one_hot(x, num_class=None):
    if not num_class:
        num_class = np.max(x) + 1
    ohx = np.zeros((len(x), num_class))
    ohx[range(len(x)), x] = 1
    return ohx


def cross_entropy_loss(x, y, reduction='mean'):
    loss = []
    for i in range(y.shape[0]):
        loss_i = -x[i, y[i]] + np.log(np.sum(np.exp(x[i])))
        loss.append(loss_i)
    dif = np.array(loss).reshape([y.shape[0], 1])
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)
    return dif


np.random.seed(10001)

x = np.random.rand(4, 100).astype('float32')
y = np.random.randint(0, 100, (4,))
np_loss = cross_entropy_loss(x, y, 'mean')
torch_loss_fn = torch.nn.CrossEntropyLoss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y).to(torch.long))
print(np_loss, torch_loss.numpy())
# 输出：4.8294697 4.829469

四、NLL损失

1、公式

负对数似然损失的思想就是使预测类别的概率最大，他的输入是概率值（sigmoid或者softmax层的输出），公式如下：

   

2、实现及对比

import torch
import numpy as np


def log_softmax(x):
    m = np.sum(np.exp(x), axis=1, keepdims=True)
    x = np.log(x / m)
    return x


def nll_loss(x, y, reduction='mean'):
    loss = []
    for i in range(y.shape[0]):
        loss_i = -x[i, y[i]]
        loss.append(loss_i)
    dif = np.array(loss)
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)
    return dif


np.random.seed(10001)

x = np.random.rand(4, 100).astype('float32')
x = log_softmax(x)
y = np.random.randint(0, 100, (4,))
np_loss = nll_loss(x, y, 'mean')
torch_loss_fn = torch.nn.NLLLoss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y).to(torch.long))
print(np_loss, torch_loss.numpy())
# 6.5572305 6.55723

五、Kullback-Leibler divergence 损失

1、公式

KL散度衡量不同分布的差异性，公式如下，它计算了预测概率和标签的分布差异：

2、实现及对比

import torch
import numpy as np


def log_softmax(x):
    m = np.sum(np.exp(x), axis=1, keepdims=True)
    x = np.log(x / m)
    return x


def kldiv_loss(x, y, reduction='mean'):
    y_log = np.log(np.where(y < 1e-3, 1e-3, y))
    dif = y * (y_log - x)
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)
    return dif


np.random.seed(10001)
x = np.random.rand(4, 100).astype('float32')
x = log_softmax(x)
y = np.random.randint(0, 2, (4, 100))
np_loss = kldiv_loss(x, y, 'mean')
torch_loss_fn = torch.nn.KLDivLoss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y).to(torch.long))
print(np_loss, torch_loss.numpy())
# 输出：2.879388073682785 2.879388

六、BCE损失

一、公式

BCE（Binary Cross Entropy Loss）用于二分类问题，该损失函数和交叉熵损失函数原理一致，公式如下：

BCEWithLogitsLoss和BCELoss原理相同，只是函数的输入有区别，本文不再验证该函数。

2、实现及对比

import torch
import numpy as np


def binary_cross_entropy_loss(x, y, reduction='mean'):
    dif = -(y * np.log(x) + (1 - y) * np.log(1 - x))
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)

    return dif

np.random.seed(10001)
x = np.random.rand(4, ).astype('float32')
y = np.random.randint(0, 1, (4, )).astype('float32')
np_loss = binary_cross_entropy_loss(x, y, 'mean')
torch_loss_fn = torch.nn.BCELoss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y))
print(np_loss, torch_loss.numpy())
# 输出：0.9325159 0.9325159

七、SMOOTHL1损失

一、公式

L1损失的导数处处相等，在网络训练时较为稳定，但是在中心值处无法求导，不方便求解。

L2损失函数处处可导，函数连续光滑，但是当输入距离中心值较远的时候，梯度较大，从而可能导致梯度下降求解过程中发生梯度爆炸，导致模型不收敛。

结合L1和L2损失函数的优点，可以得到SMOOTHL1损失函数：

2、实现及对比

import torch
import numpy as np


def smooth_l1_loss(x, y, reduction='mean'):
    rel = np.abs(x - y)
    dif = rel - 0.5
    dif[rel < 1] = 0.5 * np.square(rel)[rel < 1]
    if reduction == 'mean':
        return np.mean(dif)
    elif reduction == 'sum':
        return np.sum(dif)
    return dif


np.random.seed(10001)
x = np.random.rand(4, 3, 100)
y = np.random.rand(4, 3, 100)
np_loss = smooth_l1_loss(x, y, 'mean')
torch_loss_fn = torch.nn.SmoothL1Loss(reduction='mean')
torch_loss = torch_loss_fn(torch.from_numpy(x), torch.from_numpy(y))
print(np_loss, torch_loss.numpy())
# 输出：0.08140871478872054 0.08140871478872053