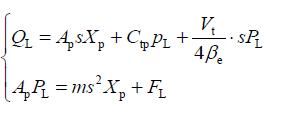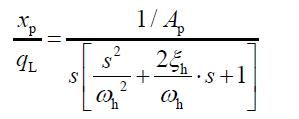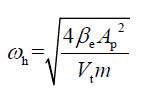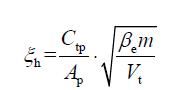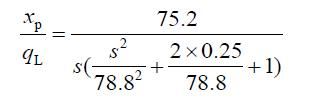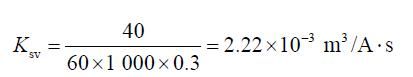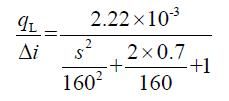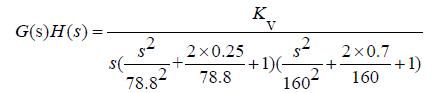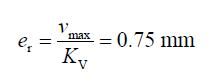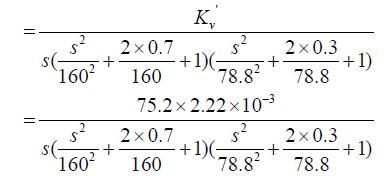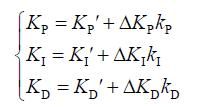一阶系统开环传递函数表达式_带钢纠偏液压系统模糊PID 控制与仿真

邹永向 吴洪明

1 带钢系统的纠偏原理

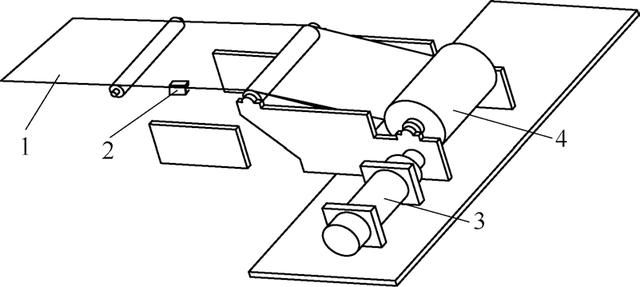
带钢纠偏液压伺服系统由液压源、电液伺服阀、放大器、伺服液压缸、卷筒、位置检测传感器[1] 等部件组成。整个液压伺服系统是一个单位负反馈系统。光电传感器检测到带钢的位置发生偏移时，将检测到的偏移信号作为这个系统的输入信号，比较器比较检测到偏移信号与液压缸推动带钢移动的位移信号，偏差信号经过放大器后作用于电液伺服阀上，液压缸根据伺服阀开口大小执行相应的动作，反复进行上述过程，直到偏差信号为0。液压源为整个系统提供动力。整个带钢纠偏系统的结构原理简图如图1 所示。

1. 带钢 2. 光电传感器 3. 液压缸 4. 卷筒

图1 带钢纠偏系统结构原理简图

2 带钢液压纠偏系统分析与建模

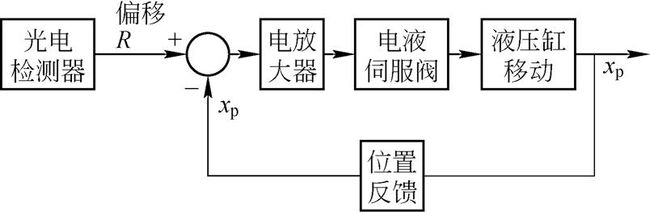
带钢液压纠偏系统伺服部分的工作原理框图[2] 如图2 所示。

图2 液压伺服控制的原理

本文以具体的带钢液压系统为例进行分析。系统的要求：

1)液压缸推动卷筒运动时的最大速度v = 25 mm/s；

2)卷筒最大质量1 m = 18 000 kg，其余部分质量2 m = 22 000 kg；

4)液压缸工作行程L = 160 mm ;

5)控制系统最大调节速度不小于25 mm/s ，系统频宽ω ＞22 rad/s，最大加速度a = 5 mm/s2，系统的最大误差e ＜±1.5 mm。

2.1 系统主要参数计算

1)供油压力的选择

该系统采用恒压变量泵，为了减小泄漏同时减少能量损失，系统采用较低的供油压力，取p s=5 MPa。

2)伺服阀的规格及其空载流量的确定

为保证伺服系统在任何情况下均满足负载的要求，以系统的最大负载进行计算

式中：F Lmax 为最大负载力，N；m 为活塞及负载折算到活塞上的总质量，kg；x p 为活塞位移，m；B p 为活塞及负载的粘性阻尼系数；K 为负载弹性刚度，N/m；F L 为作用在活塞上的任意外负载力，N。由于该液压系统没有弹性负载，且粘性阻尼系数一般很小，可以忽略不计，即K=B p=0；同时，系统的外负载力主要是摩擦力，F L=fmg ，由工程经验知，可取f =0.05，则系统的最大负载力F Lmax=19 800 N。

为保证该系统效率最大同时性能最优，取负载压力

则液压缸的有效面积

为了使该伺服系统的性能更优，可以增大液压缸活塞的面积Ap，提高其液压固有频率[2]，因此，负载压力可取更小值。选择内径32 mm、杆径25 mm 的伺服液压缸，则

伺服阀空载流量根据最大负载速度来确定，并认为最大负载速度和最大负载力同时出现。则伺服阀空载流量[2]

所选伺服阀压降Δ p =1.4 MPa，根据流量和伺服阀压降，选择额定流量为90 L/min 的伺服阀可满足系统的要求。

3)其他组成元件

由于检测器与放大器的时间常数非常小，因此光电检测器的增益

2.2 系统建模

1)动力元件的传递函数液压缸的流量连续方程为

式中：q L 为液压缸流量，x p 为目标位移，C tp 为液压缸的总泄漏系数，Vt 为液压缸处于中间位置时两腔的体积，β e 为有效体积弹性模量。液压缸和负载的力平衡方程为

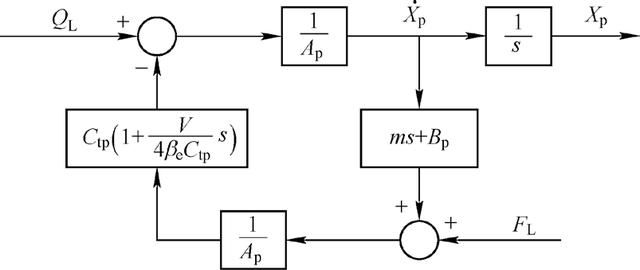
根据拉式变换方程建立如图3 所示的动力元件方块图

图3 阀控液压缸方框图

计算分析时将F L 作为恒定负载处理，则系统对QL的响应为

式中：ω h 为液压固有频率，ξ h 为液压阻尼比。由于B p 很小，可以忽略不计，则有

取V t=0.15×1.33×10-2=2.873×10-3 m3， 取β e=7×108N/m2，故动力元件的液压固有频率ω h=78.8rad/s；取ξ h=0.25，则液压动力元件的传递函数为

二级电液伺服阀的传递函数为

式中：Ksv 为空载平均流量增益，ω sv 为伺服阀固有频率，ξ sv 为伺服阀阻尼比。

伺服阀的动态参数可按样本取值，当供油压力p s=4MPa 时，空载流量为40 L/min，得到伺服阀的空载平均流量增益

由样本查得ω sv=160 rad/s，ξ sv=0.7，代入式(13)得伺服阀的传递函数为

系统的开环传递函数为

其中

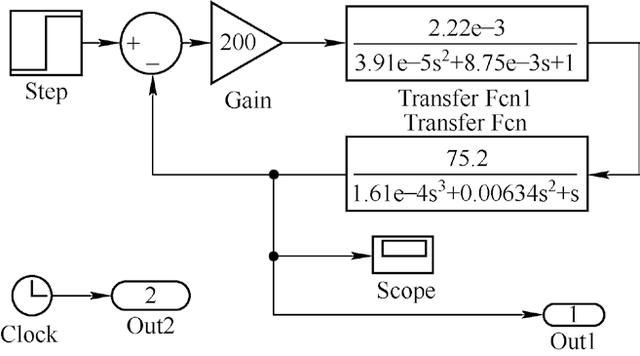
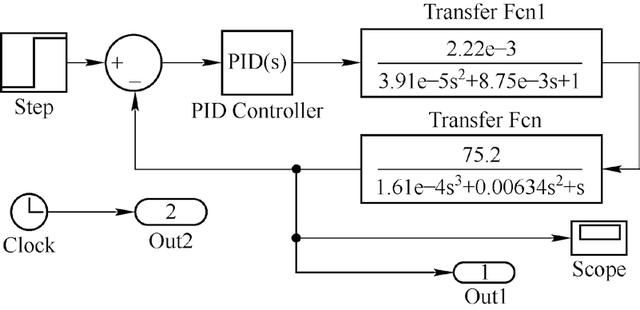
根据上述数据，绘制Simulink 仿真图形，如图4 所示。图5 是系统伯德图，图6 是系统对单位阶跃信号的响应。

图4 Simulink 仿真框图

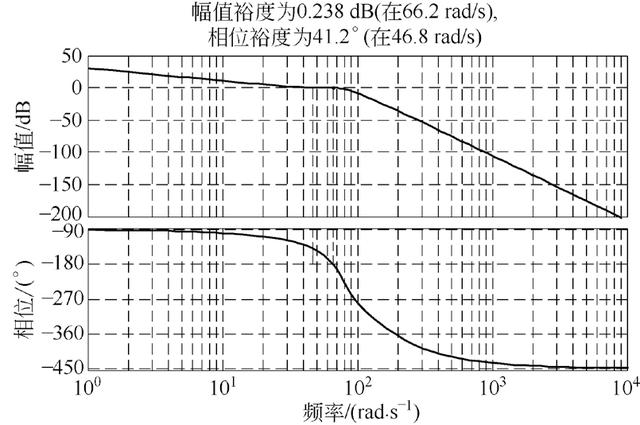
图5 带钢纠偏系统伯德图

图6 单位阶跃响应仿真结果

由运行结果可知，该伺服系统的的幅值裕度为0.239dB, 相位裕度为46.9°，系统达到最终稳态值需要的时间为10 s。系统虽然最终能够达到稳定，但系统的稳态性能很差。为了使该系统能够真正在实际控制过程中对带钢进行有效纠偏，必须对其进行优化处理。该系统的总误差

3 PID 控制器的设计

为了改善该伺服系统的性能，为该伺服系统增设PID控制器，使系统在实际控制过程中动态性能得到改善。常见的PID 参数整定的方法有衰减曲线法、经验法和临界比例度法。本文采用临界比例度法对PID 参数进行整定。该方法是基于稳定性分析的PID 整定方法，其整定思想是：首先令积分和微分环节的增益为0，然后增加KP 直至系统开始震荡，然后根据整定公式初步确定PID 的三个参数值[3]。其整定公式为

式中：Km 为系统开始振荡时的K 值，ω m 为振荡时的频率。

在该液压伺服控制中，光电检测器调节PID 控制器中的比例增益KP=K，系统的开环传递函数可以表示为

改变比例增益值，绘制每个KP 对应的单位阶跃响应图，直到其响应图处于临界振荡状态，如图7 所示。

图7 不同比例增益对应的单位阶跃响应

由图7 可知：当系统处于临界稳定时，Km=205，该点的频率ω m=66.2 rad/s。按照临界比例整定公式可知KP=123，KD=1.46，KI=2 591。

初步计算得出的PID 参数只能初步改善系统性能，可通过Matlab 中的PID 控制器调节，对PID 的参数进一步进行调整，得到更加优化的PID 参数：KP=95.7，KI=28.2，KD=1.0。加入PID 控制器后的系统开环传递函数为

Simulink 环境下建立的系统仿真模型如图8 所示，单位阶跃响应如图9 所示。

图8 PID 控制的Simulink 仿真框图

图9 加入PID 控制器后系统阶跃响应

由图9 可知，控制系统的上升时间t r=0.14 s，峰值时间t p=0.16 s，最大超调量Mp=6%，系统达到稳态值的时间为0.6 s。

4 模糊PID 控制器的设计

4.1 模糊PID 控制的特点

PID 控制具有原理简单、实现容易、适用范围广的优点。但PID 参数的整定具有一定困难，要获得较好的调节效果一般需要丰富的经验或者需要对现有的系统进行试验，而且，当确定了一组PID 的参数值后，可能不同时让系统的响应时间、超调量等参数达到最优。模糊控制具有以下优点：在使用时，即使没有建立非常精确的数学模型也不会对控制效果产生较大的影响；同时模糊控制具有较强的鲁棒性和容错能力。在PID 控制中加入模糊控制器，构成模糊PID 复合控制，可以同时具有PID 控制和模糊控制的优点：更快的动态响应特性，更小的超调量，更高的稳态精度。

4.2 模糊控制器的设计

目前广为应用的是二维的模糊控制器。本文采用二维输入三维输出的模糊控制器，将误差e 和误差的变化Δe 作为模糊控制器的输入量，以PID 的三个参数作为输出量。

4.2.1 模糊控制器模糊规则建立的基本原则

1)若误差为正同时误差的变化为正，此时应增大执行机构的控制量，以减小系统误差；

2)若误差为正同时误差的变化为负，这时执行机构本身已有消除误差的趋势，取控制量为0 或较小，可尽快消除误差且保证不超调；

3)如果误差为负而误差的变化为正，应取较小的控制量；

4)如果误差为负且误差的变化为负，此时应增大执行机构的控制量，抑制超调量。

4.2.2 PID 三个参数的作用

1)适当增大比例参数KP 的值可以加快系统的响应速度，同时减小系统的稳态误差，但系统的超调量会增加；随着KP 的进一步增大，系统的稳定性变差，最终将导致系统不稳定。

2)积分作用参数KI 的主要作用是影响消除系统的稳态误差的速度，KI 增大时系统的稳态误差消除变快。但KI 也不能过大，否则在响应过程的初期会产生积分饱和现象，当KI 减小，系统的稳态误差将难以消除，最终会影响系统的调节精度。

3)微分增益参数K D 的作用是影响系统的动态性能，调节KD 的值可以做到在响应过程中抑制偏差向任何方向的变化，提前预测偏差变化趋势。但KD 不能过大，否则会使响应过程提前制动，延长调节时间，并且会降低系统的抗干扰性能。

4.2.3 模糊PID 控制器的设计步骤

1)确定模糊控制器的输入输出变量将单位负反馈系统的误差e 和误差的变化率Δe 作为控制器的输入，将KP、P I、P D 作为控制器的输入，他们各自的模糊子集为

e ={NB,NM,NS,ZO,PS,PM,PB}；

Δe = {NB,NM,NS,ZO,PS,PM,PB}；

P K = {NB,NM,NS,ZO,PS,PM,PB}

I K = {NB,NM,NS,ZO,PS,PM,PB}

D K = {NB,NM,NS,ZO,PS,PM,PB}

2)确定变量的论域

为了方便修改PID 参数，将以上5 个变量的论域均设为[-3,3]，如图10 所示。然后在控制器的每个输入和输出前加入比例增益环节，使得其输入与输出与各自变量范围相匹配。

图 10 变量e、 Δe、K P、P I、P D 的隶属函数

3)建立模糊控制器的控制规则根据PID 各参数的作用以及模糊控制器的模糊原则，建立KP、P I、P D 模糊控制规则表，见表1 ～表3。

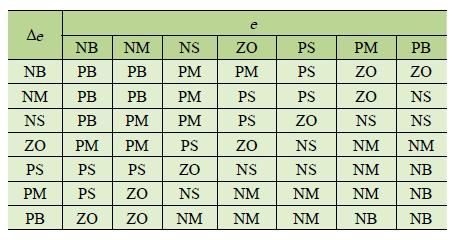
表1 K P 模糊控制规则表

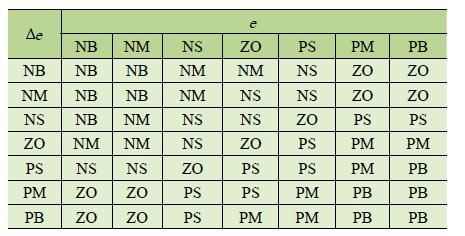
表2 K I 模糊控制规则表

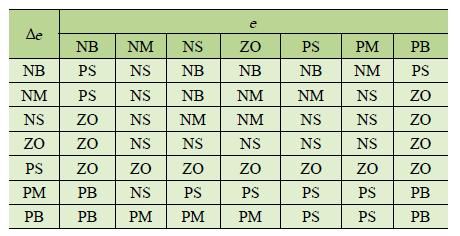
表3 K D 模糊控制规则表

输出变量的三个参数之间是相互独立没有任何关系的，其取值的决定因素是输入变量和模糊规则。

4)反模糊化为了兼顾精确性和结构复杂程度低两个方面，采用

加权平均法。

5)量化因子和比例因子的选取量化因子Ke 和Kce 决定了控制器对e 和Δe 分辨度。量化因子越大，分辨率越高，但如果取值过大，系统的响应速度会因为振荡而变得很慢[4]。对于比例因子有

式中：KP 为模糊PID 控制器输出的比例参数，KI为模糊PID 控制器输出的积分参数，KD 为模糊PID 控制器输出的微分参数，KP＇为比例参数初始值，KI＇ 为积分参数初始值，KD＇为微分参数初始值，ΔKD 为比例参数比例因子，ΔKI 为积分参数比例因子，ΔKD 为微分参数比例因子，k P 为模糊控制器输出的比例参数，k I为模糊控制器输出的比例参数，k D 为模糊控制器输出的比例参数。

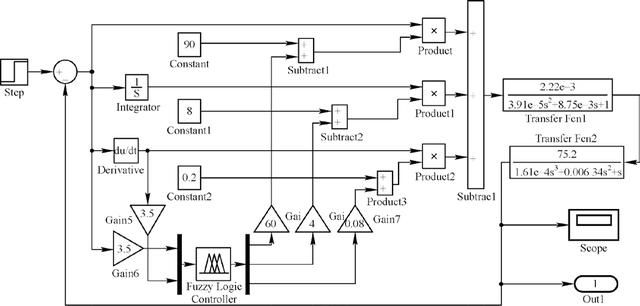
ΔKP、ΔKI、ΔKD 是将PID 控制器中的KP、KI、KD 参数按比例缩小3~6 倍，KP＇、KI＇、KD＇是将原参数按比例缩放0.2~1.1 倍。将所有的参数都确定后，在Simulink 下对伺服系统进行仿真。加入模糊PID 控制器后仿真框图和单位阶跃响应分别见图11 和图12。

图11 加入模糊PID 控制器后仿真框图

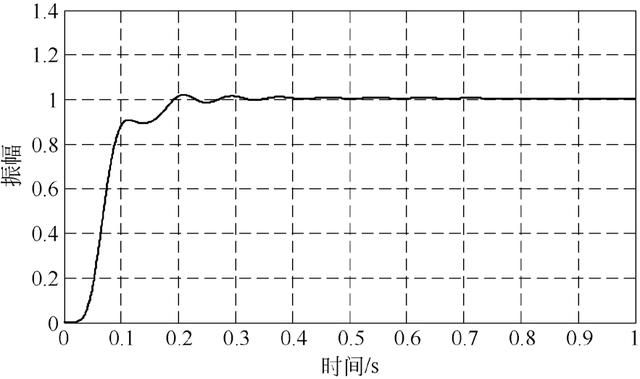
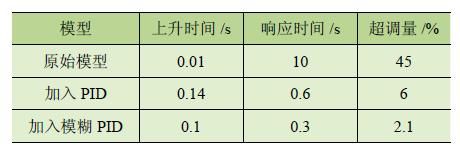
由图12 可知系统的上升时间为0.1 s，响应时间为0.3s，超调量为2.1%。将最初的系统模型、加入PID 控制器后的系统模型、加入模糊PID 控制器后的系统模型相互比较，结果见表4。

图12 加入模糊PID 控制后单位阶跃响应

表4 三种模型之间的比较

由表4 中数据可知，通过模糊PID 控制器优化之后，系统的响应时间缩短了97%，超调量降低了42.9%。

5 结束语

本文建立带钢纠偏系统的数学模型，通过PID 控制器和模糊PID 控制器逐级优化，最终使系统的控制性能得到明显的改善。结果表明将模糊PID 技术应用到该系统中是可行的。