KNN（最邻近算法）

KNN（最邻近算法）

时间：2022/5/4

0.数据集分析

测试使用的数据集为经典的鸢尾花数据集iris.有四个属性，分别为花萼长度（sepallength）、花萼宽度（sepalwidth）、花瓣长度（petallength）、花瓣宽度（petalwidth）。决策属性为种类(setosa、versicolor、virginica)。

1.算法思想

闵老师在上课时说过，机器学习的本质就是“猜”，用已知的数据去预测未知的数据，而不同的算法就是猜的方法不同。对于KNN算法而言，它猜的思想就像是“近朱者赤，近墨者黑”的思想。正如我们想了解一个人的时候就可以通过他所交的朋友来推测他是个什么样的人，KNN也是如此。KNN通过寻找离预测目标最近的对象作为预测目标的邻居。通过邻居的占比来推测预测目标的标签。

由此可见，KNN算法有一下特点：

1. 算法是比较简单，没有学习过程，也被称为惰性学习

2. 算法思想简单易懂，贴合人类思维。算法适应性也是很强，可用于分类回归，可用于多种数据。

3. 效果是非常好的，KNN算法充分利用了已知数据，对测试目标的预测准确率很高。通过测试可见，

多次测试结果KNN的正确率均在90%以上。

4. KNN也存在一个缺点，复杂度高。对于每个需要预测的目标，均需要计算其与整个训练集的距离。对于每一个测试数据, 复杂度为 O ( ( m + k ) n ) , 其中n为训练数据个数, m为条件属性个数, k为邻居个数.

5. 一般需要对数据归一化。

6. 使用过程对内存要求较高，最好是能将数据集全部存入内存中，若是内存空间较小，频繁的进行IO操作，则对算法的时间影响较大。

2.算法流程：

1. 读入数据集，使用weka.jar包进行数据读取存储。
2. 拆分数据集，按一定比例划分为训练集与测试集。
3. 预测测试集：
   1. 取出一个测试对象
   2. 计算测试对象到训练集中训练对象的距离，这里提供两种距离度量：欧式距离和曼哈顿距离；
   3. 选取距离最近的K个邻居
   4. 投票：这里使用的是简单投票，统计邻居种类个数。
   5. 投票最多的标签即为预测对象的标签
4. 计算预测准确度。

3.代码部分

/**
 * KNN.java
 *
 * @author zjy
 * @date 2022/5/3
 * @Description: KNN算法的学习
 * @version V1.0
 */
package swpu.zjy.ML.KNN;

import weka.core.Instances;

import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Random;

public class KNN {
    /**
     * 定义KNN使用的距离度量
     */
    //曼哈顿距离
    public static final int MANHATTAN = 0;
    //欧几里得距离
    public static final int EUCLIDEAN = 1;

    public static int distanceMeasure = EUCLIDEAN;

    //邻居数量：K ;默认为7
    public static int numNeighbors = 7;

    //数据集对象 用以存储整个数据集
    Instances datasets;

    /**
     * 训练集与测试集实体
     * 这里老师采用的方法是只存储一个元组的下标，用索引的形式存储训练集与测试集，
     * 这是之前所没有使用形式，经过实际测试，这种方法比使用对象存储数据的方式要更快且更加节省内存。
     */
    //训练集
    int[] trainingSet;
    //测试集
    int[] testingSet;

    //预测标签 ，存储KNN预测的结果
    int[] predictions;

    //随机数生成器
    public static Random random = new Random();

    /**
     * KNN构造方法，通过传入数据文件路径，构造数据集
     *
     * @param dataSetFileName 数据集文件路径
     */
    public KNN(String dataSetFileName) {
        try {
            FileReader fileReader = new FileReader(dataSetFileName);
            //使用weka包读取数据集
            datasets = new Instances(fileReader);
            //设置数据集决策属性 datasets.numAttributes()获取数据集属性个数
            //本次使用的鸢尾花数据集，将最后一项作为决策属性
            datasets.setClassIndex(datasets.numAttributes() - 1);
            fileReader.close();
        } catch (IOException e) {
            e.printStackTrace();
            System.exit(0);
        }
    }

    /**
     * 设置邻居个数，默认是7，可由用户自己设定
     *
     * @param numNeighbors 邻居个数
     */
    public static void setNumNeighbors(int numNeighbors) {
        KNN.numNeighbors = numNeighbors;
    }

    /**
     * 设置距离度量选择
     *
     * @param distanceMeasure 距离度量类型
     */
    public static void setDistanceMeasure(int distanceMeasure) {
        KNN.distanceMeasure = distanceMeasure;
    }

    /**
     * 洗牌，将数据集随机打乱，以便后续划分训练集与测试集，采用索引方式
     *
     * @param numInstance 数据个数
     * @return 打乱后的数据集
     */
    public static int[] shuffle(int numInstance) {
        //构造索引数组
        int[] tempIndices = new int[numInstance];
        //初始化索引数组
        for (int i = 0; i < numInstance; i++) {
            tempIndices[i] = i;
        }
        //开始洗牌
        int tempFirst, tempSecond, tempIndex;
        for (int i = 0; i < numInstance; i++) {
            //随机选取下标
            tempFirst = random.nextInt(numInstance);
            tempSecond = random.nextInt(numInstance);

            //Swap
            tempIndex = tempIndices[tempFirst];
            tempIndices[tempFirst] = tempIndices[tempSecond];
            tempIndices[tempSecond] = tempIndex;
        }
        return tempIndices;
    }

    /**
     * 训练集与测试集的划分，按照给定的比例分割
     *
     * @param trainingFraction 训练集所占比例。
     */
    public void splitTrainingandTesting(double trainingFraction) {
        int tempSize = datasets.numInstances();
        //洗牌
        int[] tempIndices = shuffle(tempSize);
        //得到训练集长度
        int tempTrainingSize = (int) (tempSize * trainingFraction);

        trainingSet = new int[tempTrainingSize];
        testingSet = new int[tempSize - tempTrainingSize];

        //划分数据集
        for (int i = 0; i < tempTrainingSize; i++) {
            trainingSet[i] = tempIndices[i];
        }
        for (int i = 0; i < tempSize - tempTrainingSize; i++) {
            testingSet[i] = tempIndices[tempTrainingSize + i];
        }
    }

    /**
     * 计算两个实例的距离，根据所选距离度量来计算
     *
     * @param dataA 实例A
     * @param dataB 实例B
     * @return 二者距离
     */
    public double distance(int dataA, int dataB) {
        double resultDistance = 0;
        double tempDistance = 0;
        switch (distanceMeasure) {
            case MANHATTAN:
                /**
                 * 曼哈顿距离，也叫城市距离；distance=|x1-x2|+|y1-y2|
                 */
                for (int i = 0; i < datasets.numAttributes() - 1; i++) {
                    tempDistance = datasets.instance(dataA).value(i) - datasets.instance(dataB).value(i);
                    if (tempDistance < 0) {
                        resultDistance -= tempDistance;
                    } else {
                        resultDistance += tempDistance;
                    }
                }
                break;
            case EUCLIDEAN:
                /**
                 * 欧式距离，distance=sqrt((x1-x2)^2+(y1-y2)^2)
                 * 对于欧式距离，本来应该要开方，但这里的距离度量并不是为了获取精确的数据，
                 * 只是为了比较大小，所有不用开方以减少计算
                 */
                for (int i = 0; i < datasets.numAttributes() - 1; i++) {
                    tempDistance = datasets.instance(dataA).value(i) - datasets.instance(dataB).value(i);
                    resultDistance += tempDistance * tempDistance;
                }
                break;
            default:
                System.out.println("未知的距离度量");
                System.exit(0);
        }
        return resultDistance;
    }

    /**
     * 寻找当前数据的K个邻居
     *
     * @param currentData 当前数据索引
     * @return 当前数据的K个邻居
     */
    public int[] findNeighbors(int currentData) {
        //存放当前数据所有距离
        double[] tempDistances = new double[trainingSet.length];
        //存放K个邻居
        int[] neighbors = new int[numNeighbors];
        double tempNearDistance = 0;
        int tempindex = 0;

        //计算距离
        for (int i = 0; i < trainingSet.length; i++) {
            tempDistances[i] = distance(currentData, i);
        }
        //寻找邻居
        for (int i = 0; i < numNeighbors; i++) {
            tempNearDistance = Double.MAX_VALUE;
            for (int j = 0; j < trainingSet.length; j++) {
                if (tempDistances[j] == -1)
                    continue;
                if (tempDistances[j] < tempNearDistance) {
                    tempNearDistance = tempDistances[j];
                    tempindex = j;
                }
            }
            neighbors[i] = tempindex;
            tempDistances[tempindex] = -1;
        }

        //System.out.println("The nearest of " + currentData + " are: " + Arrays.toString(neighbors));
        return neighbors;
    }

    /**
     * 简单投票，无权重统计邻居类别
     *
     * @param neighbors K个邻居
     * @return 预测类别
     */
    public int simpleVoting(int[] neighbors) {
        int[] tempVotes = new int[datasets.numClasses()];
        for (int i = 0; i < neighbors.length; i++) {
            tempVotes[(int) datasets.instance(neighbors[i]).classValue()]++;
        }

        int tempMaxVotingIndex = 0;
        int tempMaxVoting = 0;
        for (int i = 0; i < tempVotes.length; i++) {
            if (tempVotes[i] > tempMaxVoting) {
                tempMaxVoting = tempVotes[i];
                tempMaxVotingIndex = i;
            }
        }
        return tempMaxVotingIndex;
    }

    /**
     * 预测整个测试集
     */
    public void predict() {
        predictions = new int[testingSet.length];
        for (int i = 0; i < testingSet.length; i++) {
            predictions[i] = predict(testingSet[i]);
        }
    }

    /**
     * 预测单个数据标签
     *
     * @param paraIndex 数据索引
     * @return 数据预测标签
     */
    public int predict(int paraIndex) {
        int[] tempNeighbors = findNeighbors(paraIndex);
        int resultPrediction = simpleVoting(tempNeighbors);

        return resultPrediction;
    }

    /**
     * 展示预测结果
     */
    public void showPredicts() {
        for (int i = 0; i < testingSet.length; i++) {
            System.out.println("数据：" + testingSet[i] + ",预测标签：" + predictions[i] + ",实际标签：" + datasets.instance(testingSet[i]).classValue());
        }
    }

    /**
     * 计算预测正确率
     *
     * @return 正确率
     */
    public double getAccuracy() {
        double tempCorrect = 0;
        for (int i = 0; i < predictions.length; i++) {
            if (predictions[i] == datasets.instance(testingSet[i]).classValue())
                tempCorrect++;
        }
        return tempCorrect / testingSet.length;
    }

    public static void main(String[] args) {
        KNN knnTest = new KNN("E:\\DataSet\\iris.arff");
        knnTest.splitTrainingandTesting(0.8);
        for (int i = 3; i < 10; i++) {
            KNN.setNumNeighbors(i);
            knnTest.predict();
//        knnTest.showPredicts();

            System.out.printf("K=" + i + ",正确率为：%.2f%% \n", (knnTest.getAccuracy() * 100));
        }
    }

}

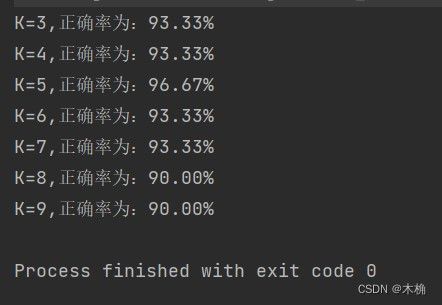
4.运行结果

对于K的选取对于KNN算法的效果影响还是比较明显的；

5.优化思考

对于KNN算法的优化可以从它的主要算法步骤入手

1. 首先是计算距离。在这一步骤中我们可以通过选取更加合适的距离度量来进行距离计算，以期得到更精确的预测。在闵老师的推荐下，后面学习了基于M-distance的KNN。
2. 其次是选取K个邻居。在这里可以通过引入排序算法实现选取时间复杂度的降低。使用插入排序选取K个的时间复杂度为：O(KN)；在张星移同学的测试中，引入大小为N的堆，对单个测试集的中心结点测试的复杂度可以从O(kN)优化为O(k+N)。总复杂度为O(M(N+k))。由此可见采用更高效的排序算法可优化KNN的时间复杂度。
3. 最后则是在投票环节，除了简单投票外，还可以采用基于距离的加权投票，距离越近权重越高。借此增加预测准确率。

KNN算法的效果影响还是比较明显的；