《LC刷题总结》——动态规划
动态规划题目汇总
动态规划模板
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组初始化
- 确定遍历顺序
一维的:
509. 斐波那契数——一维数组
题目:F(n) = F(n - 1) + F(n - 2)
class Solution:
def fib(self, n: int) -> int:
dp = [0 for i in range(n+2)] # 1. 确定dp数组
dp[1] = 1 # 2. 初始化
for i in range(2,n+1): # 3. 确定遍历顺序
dp[i] = dp[i-1] + dp[i-2] # 4. 递推公式
return dp[n]
二维:
62. 不同路径——二维数组
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0 for _ in range(n+1)] for _ in range(m+1)] # 1. 定义dp数组
for i in range(m): # 2. 初始化
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
for i in range(1,m+1): # 3. 遍历顺序
for j in range(1,n+1):
dp[i][j] = dp[i-1][j] + dp[i][j-1] # 4. 递推公式
print(dp)
return dp[m-1][n-1]
基础问题
746. 使用最小花费爬楼梯
题目:
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费
思路:
首先定义dp,dp[i]表示的是达到第i个台阶的总花费
初始化,dp[1],dp[2] = cost[0],cost[1]
返回结果是最后两个台阶的最小值。
代码:
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
# dp = [0] * (len(cost)+1)
dp[1],dp[2] = cost[0],cost[1]
for i in range(3,len(cost)+1):
dp[i] = cost[i-1] + min(dp[i-1],dp[i-2])
return min(dp[-1],dp[-2])
题目:
思路:
代码:
在这里插入代码片
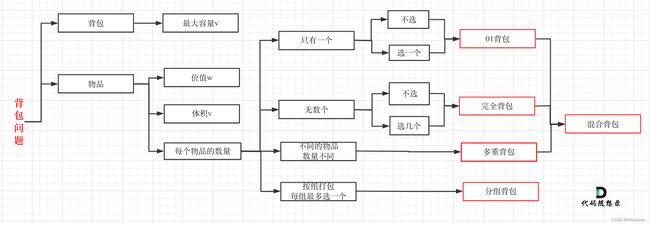
背包问题
关于背包问题,就是一个有限制的背包,如何让装入物品价值最大化的问题。
抓哟分为0-1背包和完全背包。
- 0-1背包:每个物品只有一个
- 完全背包:物品可以重复选
1.1 01背包
物品:重量w-价值v,只有一件
背包:负重W
- dp[j]定义:对于背包j的最大价值
- 递推公式:dp[j] = max(dp[j], dp[j - weight[i]] +value[i])
- dp初始化:dp[0]=0
- 遍历顺序:外层:物品,正序;内层:背包,逆序。
def bag01_problem(self):
# 初始化: 全为0
dp = [0] * (self.bag_weight + 1)
# 外层遍历物品,因为背包倒叙,如果背包在外层,对于每个j背包,只能放一个物品了
for i in range(len(self.weight)):
# 为了保证物品在每个j背包只放入一次,所以背包容量必须倒序,防止大背包包括小背包造成物品多次取样
for j in range(self.bag_weight, self.weight[i]-1, -1):
dp[j] = max((dp[j], dp[j-self.weight[i]]+self.value[i]))
return dp[-1]
416. 分割等和子集
问题:
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
思路:
只需要找到一个组合和为原数组和的一半a即可
把a看作背包容量,数组的数字看作价值和重量,如果对于a的背包恰好存在最大价值是a的,则可以构成。
每个数字最多用一次,转换成01背包
代码
class Solution:
def canPartition(self, nums: List[int]) -> bool:
a = int(sum(nums) / 2)
if sum(nums) % 2 != 0:
return False
dp = [0] * (a+1)
for i in range(len(nums)):
for j in range(a, nums[i]-1,-1):
dp[j] = max(dp[j], dp[j-nums[i]]+nums[i])
return dp[-1] == a
1049. 最后一块石头的重量 II
问题:
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
思路
将石头分成两堆,尽可能重量接近即可。
所以,和上题类似,将和的一半作为背包重量进行计算最大值。
代码
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
target = sum(stones)//2
dp = [0] * (target+1)
for i in range(len(stones)):
for j in range(target, stones[i]-1,-1):
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
print(dp)
return (sum(stones)-dp[-1])-dp[-1]
494. 目标和——计算组合数
思路
转换为 找两个子集s1,s2,成为s1-s2=target。
进一步,s1-s2+s1+s2 = traget + s1+s2
得到 2s1 = traget+sum.
这个s1就是背包的重量,需要计算充满这个背包有几种方式。
也就是经典的计算组合数的方式。
还有个雷点就是边界条件。通过上述知道,s1必然是个整数,所以如果taget+sum是个奇数,则不存在组合,返回0。
此外,如果target的abs 大于 sum,也不行。比如[1,1,1], 10。无论如何也凑不起来。
代码
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
s = sum(nums)
s1 = (s+target)/2
if (s+target) % 2 == 1:
return 0
if abs(target) > s:
return 0
dp = [0] * (int(s1)+1)
dp[0] = 1
for i in range(len(nums)):
for j in range(int(s1), nums[i]-1, -1):
dp[j] += dp[j-nums[i]]
return dp[-1]
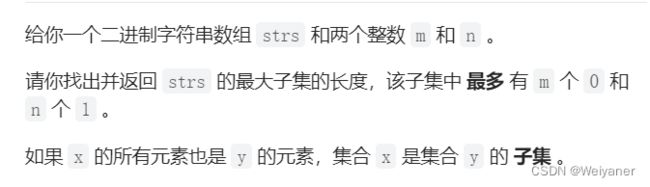
474. 一和零——二维背包
思路
mn的个数就是背包的容量,所以本题是一个二位背包问题。只需要dp变成2为数组,然后再进行背包循环时多加一层循环。依旧是逆序。
代码
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
def get01(s):
s = [i for i in s]
return s.count('1'), s.count('0')
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(len(strs)):
n1, n0 = get01(strs[i])
for j in range(m, n0-1,-1):
for k in range(n,n1-1,-1):
dp[j][k] = max(dp[j][k], dp[j-n0][k-n1]+1)
return dp[-1][-1]
1.2 完全背包
物品:重量w-价值v,有无数件
背包:负重W
- dp[j]定义:对于背包j的最大价值
- 递推公式:dp[j] = max(dp[j], dp[j - weight[i]] +value[i])
- dp初始化:dp[0]=0
- 遍历顺序:外层:物品,正序;内层:背包,正序。
对于纯完全背包问题,内外层循环都一样,都是正序遍历,为了保证物品有无数个。
def test_complete_pack1():
dp = [0]*(bag_weight + 1)
for i in range(len(weight)):
for j in range(weight[i], bag_weight + 1):
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]
print(dp[bag_weight])
# 先遍历背包,再遍历物品
def test_complete_pack2():
dp = [0]*(bag_weight + 1)
for j in range(bag_weight + 1):
for i in range(len(weight)):
if j >= weight[i]:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bag_weight])
但是对于具体问题,比如组合排列数的问题,就需要改变遍历顺序了。
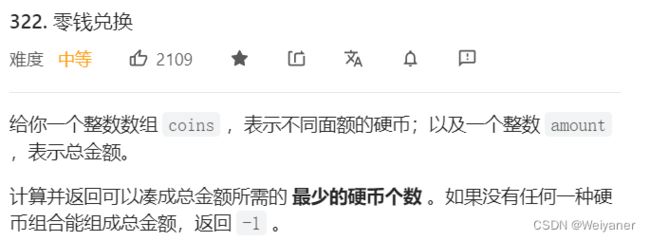
322. 零钱兑换
思路:
- 硬币数量无限
- 有背包限制 ——》完全背包问题
- 计算最小硬币数,初始化必须无穷大
- 递推公式:dp = min(dp,dp[j-coins[i]]+1)
代码:
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount+1)
dp[0] = 0
for j in range(1,amount+1):
for i in range(len(coins)):
if j >= coins[i]:
dp[j] = min(dp[j],dp[j-coins[i]]+1)
return dp[-1] if dp[-1] < 100000 else -1
139.单词分割
思路:
看作是完全背包问题
dp[j]代表着遍历到第j个字符,是否能被分隔
发现如果遍历到第i、个分隔字符,如果dp[j-len(i)]为真的话,且这部分也在字分隔典中,那么dpj也为真。
递推公式的确定:
if dp[j-len(i)] and s[j-len(i):j] in wordDict:
dp[j] = True
代码
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
dp = [False] * (len(s)+1)
dp[0] = 1
for j in range(1,len(s)+1):
for i in wordDict:
if j>=len(i):
if dp[j-len(i)] and s[j-len(i):j] in wordDict:
dp[j] = True
return dp[-1]
组合类
递推公式:
dp[j] += dp[j - nums[i]]
组合:
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
dp[j] += dp[j - coins[i]];
}
}
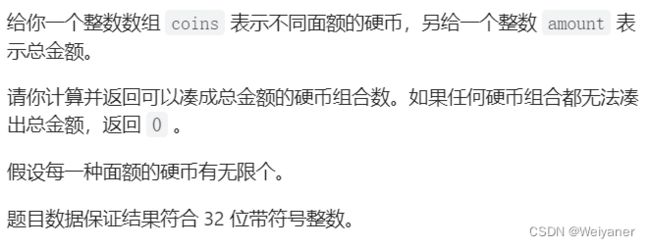
518. 零钱兑换 II——组合数
思路
完全背包中的组合问题
先遍历物品,在遍历背包
代码
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0] * (amount+1)
dp[0] = 1
for i in range(len(coins)):
for j in range(coins[i], amount+1):
dp[j] += dp[j-coins[i]]
return dp[-1]
排列类
for (int j = 0; j <= amount; j++) { // 遍历背包容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}
377. 组合总和 Ⅳ
思路:
无限次取数,且排列有效,就是完全背包的排列问题
背包在外,物品在内。
代码
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0]* (target+1)
dp[0] = 1
for j in range(target+1):
for i in range(len(nums)):
if j >= nums[i]:
dp[j] += dp[j-nums[i]]
return dp[-1]
打家劫舍
198. 打家劫舍
思路:
不要复杂化,就是普通的动态规划
对于当前i位置,选i-2+本身还是i-1.取最大值。
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
daima:
class Solution:
def rob(self, nums: List[int]) -> int:
dp = [0] * len(nums)
dp[0] = nums[0]
if len(nums) < 2:
return dp[0]
dp[1] = max(nums[0],nums[1])
for i in range(2,len(nums)):
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
return dp[-1]
213. 打家劫舍 II
房子首尾相接,计算最大窃取金额
思路:
既然首尾相接,就只能考虑其中一个,将原数组拆分为2个,只考虑首或者只考虑尾。然后取其中的最大值即可。
子序列问题
一维
300. 最长递增子序列
思路:
dp[i]:截止到i的最长子序列长度
由于比i小的不确定上一个数字位置,所以需要对i之前都进行遍历,作为内层。外圈对i遍历。
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j]+1)
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
dp = [1] * len(nums)
if len(nums)==1:
return 1
for i in range(1,len(nums)):
for j in range(0,i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j]+1)
return max(dp)
53.最大子数组和
思路:
主要是看i之前的和 以及 现在nums[i]的收益那个大。
定义:
dp[i]:以i结尾的连续和。
递推条件:dp[i] = max(nums[i], dp[i-1]+nums[i])
由于不一定是末尾数结尾的连续值,所以取max res
代码
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [0] * len(nums)
dp[0] = nums[0]
if len(nums) == 1:
return dp[0]
for i in range(1, len(nums)):
dp[i] = max(nums[i], dp[i-1]+nums[i])
return max(dp)
二维
718. 最长重复子数组
思路:
涉及到两个字符串,所以dp应该是2维的。
要求是最长连续子串,连续保证了,如果当前ij相等,从i-1和j-1即可推断。所以定义:
dp[i][j]:以i和j位置为重复数字的最长子串长度
初始化全部为0
代码:
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
dp = [[0]*(1+len(nums2)) for _ in range(1+len(nums1))]
for i in range(1,len(nums1)+1):
for j in range(1,len(nums2)+1):
if nums1[i-1] == nums2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
res = 0
for i in dp:
for j in i:
res = max(res,j)
return res
1143. 最长公共子序列
思路:
和上题唯一的区别在于本题不要求连续子串,二是计算子序列。
所以条件放松了许多,对应的
d[i][j]:以i,j结尾的最长公共子序列。
递推条件:当相等时,为前一位置+1
不相等时,就是左边或者上边的值的最大值。
if text1[i-1] == text2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
代码
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
dp = [[0]*(1+len(text2)) for _ in range(1+len(text1))]
for i in range(1,len(text1)+1):
for j in range(1,len(text2)+1):
if text1[i-1] == text2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
583. 两个字符串的删除操作
思路:
字符串变相同,变最长公共子序列。所以长度各减去子序列长度即时操作的次数。
和上题一样。
1035. 不相交的线
silu:
由于要求不交叉,也就是看作时计算最长公共子序列
392.判断子序列
思路:
dp[i][j]:截止到i,j,是否是子序列。
判断当前i,j。如果一样,则时i-1,j-1的状态
不一样,就是左边i,j-1状态。

代码:
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
dp = [[False] * (1+len(t)) for _ in range(1+len(s))]
for i in range(len(t)+1):
dp[0][i] = True # 空字符一定是子序列。
for i in range(1,len(s)+1):
for j in range(1,len(t)+1):
if t[j-1] == s[i-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = dp[i][j-1]
return dp[-1][-1]
115.不同的子序列
思路
dpij代表ij结尾的子序列个数,所以递推公式:
dp[i][j] = dp[i-1][j-1] + dp[i][j-1]
因为,dp[i-1][j-1]代表不带i的个数,那么加上i也是这么多
dp[i][j-1]是之前的含i的个数。
代码
class Solution:
def numDistinct(self, s: str, t: str) -> int:
dp = [[0]*(len(s)+1) for _ in range(len(t)+1)]
for i in range(len(s)+1):
dp[0][i] = 1
for i in range(1,len(t)+1):
for j in range(1,len(s)+1):
if t[i-1] == s[j-1]:
dp[i][j] = dp[i-1][j-1] + dp[i][j-1]
else:
dp[i][j] = dp[i][j-1]
return dp[-1][-1]
72. 编辑距离
思路:
遇到两个字符串的,必然需要二维dp数组。
观察规律可以看到:
8
当ij一样时候,不用操作,需要i-1,j-1.
if (word1[i - 1] == word2[j - 1])
dp[i][j] = dp[i - 1][j - 1]
但不一样的时候,三个方向分别代表了不同的操作:
- 上:删除
- 左:新增
- 左上:替换
所以:
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1
代码:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
dp = [[0]* (len(word2)+1) for _ in range(len(word1)+1)]
for i in range(len(word2)+1):
dp[0][i] = i
for j in range(len(word1)+1):
dp[j][0] = j
for i in range(1,len(word1)+1):
for j in range(1,len(word2)+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
return dp[-1][-1]
647.回文子串
思路:
暴力解法:
两层for循环,遍历区间起始位置和终止位置,然后判断这个区间是不是回文。
时间复杂度:O(n^3)
动态规划解法:
对于ij,如果i+1,j-1是回文,那么他也是。
基于此,遍历顺序i要从后往前,j从i到后。这样才可以i位置知道i+1的情况。
代码
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
c = 0
for i in range(len(s)-1,-1,-1):
for j in range(i,len(s)):
if s[i] == s[j]:
if j-i <= 1:
dp[i][j] = True
c += 1
elif dp[i+1][j-1]:
dp[i][j] = True
c+=1
return c
516. 最长回文子序列
思路:
和回文子串相比,最长回文子序列的条件送了一点,在于:
对于ij相等,不一定要求i+1,j-1是回文串,而是里面的回文子序列长度+2即可。
如果i,j不相等,那么就等于上一位置的状态,也就是i+1,j和i,j-1的最大值。
由此得到递推公式:
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j],dp[i][j-1])
遍历顺序依旧是i倒叙,j正序。但是j要从i+1开始,
代码:
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
dp = [[0] * (len(s)) for _ in range(len(s))]
for i in range(len(s)):
dp[i][i] = 1
res = 0
if len(s) ==1:
return 1
for i in range(len(s)-1,-1,-1):
for j in range(i+1,len(s)):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j],dp[i][j-1])
res = max(res, dp[i][j])
return res
其中,也可以这样:
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
dp = [[0] * (len(s)) for _ in range(len(s))]
res = 1
for i in range(len(s)-1,-1,-1):
for j in range(i,len(s)):
if s[i] == s[j]:
if j==i:
dp[i][j] = 1
else:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j],dp[i][j-1])
res = max(res, dp[i][j])
return res