Matplotlib和Seaborn(散点图、热图、小提琴图、箱线图)
文章目录
- 散点图和相关性:
-
- 散点图:
- 重叠、透明度和抖动:
- 热图:
- 小提琴图:
- 箱线图
散点图和相关性:
散点图:
如果我们想研究两个数值变量之间的关系,通常会选择散点图。在散点图中,每个数据点都单独表示为一个点,x 轴对应一个特征值,y 轴对应另一个特征值。创建散点图的一个基本方式是利用 Matplotlib 的 scatter 函数:
plt.scatter(data = df, x = 'num_var1', y = 'num_var2')
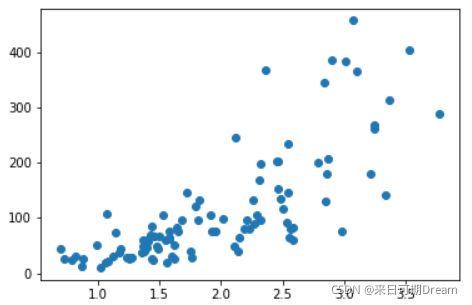
可以在这两个变量之间看到一个大致上的正向关系,x 轴的值越高,y 轴上的变量值也增大。
替代方法:
Seaborn 的 regplot 函数可以创建具有回归拟合的散点图:
sb.regplot(data = df, x = 'num_var1', y = 'num_var2')
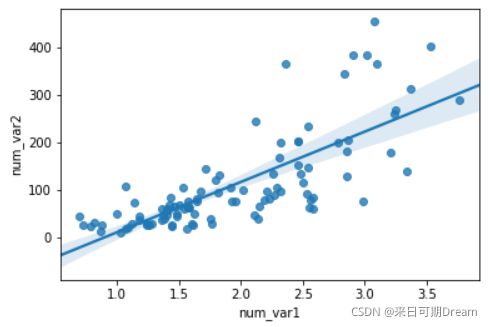
默认的回归函数是线性回归,并且包含回归估计置信区间(阴影部分)。因为上面图表的情况看起来像 \text{log}(y) \propto xlog(y)∝x 关系(也就是 x 与 log(y) 存在线性相关),因此用原始单位绘制回归线不合适。如果我们不关心回归线,那么可以在 regplot 函数调用中设置 reg_fit = False。如果我们想对观察到的数据相关性拟合回归线,需要变换数据。
def log_trans(x, inverse = False):
if not inverse:
return np.log10(x)
else:
return np.power(10, x)
sb.regplot(df['num_var1'], df['num_var2'].apply(log_trans))
tick_locs = [10, 20, 50, 100, 200, 500]
plt.yticks(log_trans(tick_locs), tick_locs)
在此例中,regplot 的参数 x 和 y 直接设为了从 DataFrame 中提取的 Series。

重叠、透明度和抖动:
如果要绘制大量数据点,或者数值变量是离散型的,那么直接使用散点图可能无法呈现足够的信息。图形可能会出现重叠,由于大量数据重叠到一起,导致很难看清变量之间的关系。
plt.scatter(data = df, x = 'disc_var1', y = 'disc_var2')
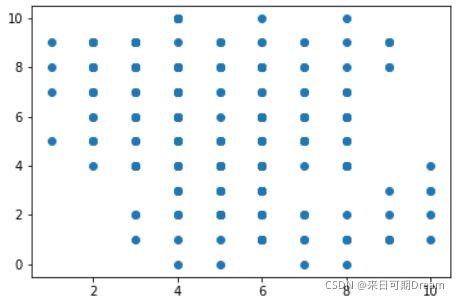
在上图中,我们可以推断出两个变量负相关,但是数据的变化程度和关系强度并不明显。在这种情形下,我们需要应用透明度和抖动,使散点图能呈现更多的信息。可以通过在 scatter 函数调用时添加 “alpha” 参数来表示透明度,“alpha” 的值可以介于 0(完全透明,不可见) 到 1(完全不透明)之间。
plt.scatter(data = df, x = 'disc_var1', y = 'disc_var2', alpha = 1/5)
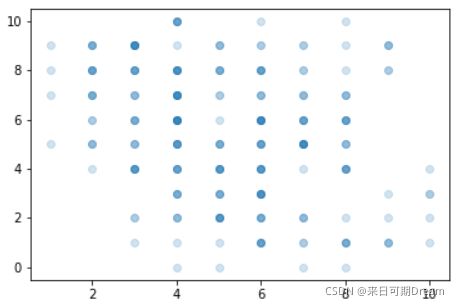
重叠的点越多,图像颜色就越深。从图中可以看出,两个数值变量之间存在一定的负相关关系。x 轴上 0 和 10 的值比中间的值要少很多。
除了设置透明度,我们还可以通过抖动使每个点稍微偏离真实值所对应的位置。这并不是 scatter 函数中的直接选项,但是 seaborn 的regplot 函数有这个内置选项。可以单独添加 x 轴和 y 轴抖动,不会影响到回归方程的拟合情况,如果编写下面的代码:
sb.regplot(data = df, x = 'disc_var1', y = 'disc_var2', fit_reg = False,
x_jitter = 0.2, y_jitter = 0.2, scatter_kws = {'alpha' : 1/3})
抖动设置将导致每个点在真实值的 ±0.2 范围内抖动。注意透明度设置已经更改为分配给 “scatter_kws” 参数的字典。这样设置可以将该透明度特别指定到regplot 函数的 scatter 组件。
热图:
热图是直方图的二维版本,可以替代散点图。和散点图一样,要绘制的两个数值变量位于两个坐标轴上。和直方图类似,图表区域被划分为网格,累计每个网格的数据点数量。因为没有空间表示条形的高度,因此用网格颜色表示计数。你可以通过 Matplotlib 的 hist2d 函数实现热图。
plt.figure(figsize = [12, 5])
# left plot: scatterplot of discrete data with jitter and transparency
plt.subplot(1, 2, 1)
sb.regplot(data = df, x = 'disc_var1', y = 'disc_var2', fit_reg = False,
x_jitter = 0.2, y_jitter = 0.2, scatter_kws = {'alpha' : 1/3})
# right plot: heat map with bin edges between values
plt.subplot(1, 2, 2)
bins_x = np.arange(0.5, 10.5+1, 1)
bins_y = np.arange(-0.5, 10.5+1, 1)
plt.hist2d(data = df, x = 'disc_var1', y = 'disc_var2',
bins = [bins_x, bins_y])
plt.colorbar();
注意,因为有两个变量,因此 “bins” 参数为一个列表,其中的两个值分别指定两个维度的分组边界。和单变量直方图一样,选择合适的分组区间很重要。我们添加了 colorbar 函数调用,在图表的一侧添加色条,显示计数与颜色的映射。

随着热图中的颜色越来越亮,从蓝色变成黄色,相应单元格中的数据量越来越多。
热图还可以用作条形图的二维版本,按照两个分类变量(而不是数值变量)的计数绘制图表。seaborn 中的函数 heatmap 专门用于绘制分类热图。稍后我们将在这节课的“分组条形图”部分详细讲解这方面的知识。
其他版本
要选择其他调色板,可以在 hist2d 中设置 “cmap” 参数。设置调色板的最简单方式是使用字符串引用内置 Matplotlib 调色板。暂时我们先通过一个示例了解,设置 cmap = 'viridis_r' 可以将默认的 “viridis” 修改为反向的调色板。
此外,我想区分计数为零的单元格和计数非零的单元格。“cmin” 参数指定了单元格要绘制出来的最小数据量。在 hist2d 调用中添加 cmin = 0.5 参数后,只有包含一个数据点以上的单元格才会有颜色
bins_x = np.arange(0.5, 10.5+1, 1)
bins_y = np.arange(-0.5, 10.5+1, 1)
plt.hist2d(data = df, x = 'disc_var1', y = 'disc_var2',
bins = [bins_x, bins_y], cmap = 'viridis_r', cmin = 0.5)
plt.colorbar()

如果你有大量数据,可能需要向图表中的单元格添加注释,表示每个单元格的数据量。在hist2d 调用中,我们必须挨个地添加文本标注,就像在上节课挨个地向条形图中添加文本标注一样。我们可以直接通过 hist2d 返回的结果得出要标注的计数,该函数返回的结果不仅包括图表对象,还包括计数的数组和两个分组区间的向量。
# hist2d returns a number of different variables, including an array of counts
bins_x = np.arange(0.5, 10.5+1, 1)
bins_y = np.arange(-0.5, 10.5+1, 1)
h2d = plt.hist2d(data = df, x = 'disc_var1', y = 'disc_var2',
bins = [bins_x, bins_y], cmap = 'viridis_r', cmin = 0.5)
counts = h2d[0]
# loop through the cell counts and add text annotations for each
for i in range(counts.shape[0]):
for j in range(counts.shape[1]):
c = counts[i,j]
if c >= 7: # increase visibility on darkest cells
plt.text(bins_x[i]+0.5, bins_y[j]+0.5, int(c),
ha = 'center', va = 'center', color = 'white')
elif c > 0:
plt.text(bins_x[i]+0.5, bins_y[j]+0.5, int(c),
ha = 'center', va = 'center', color = 'black')
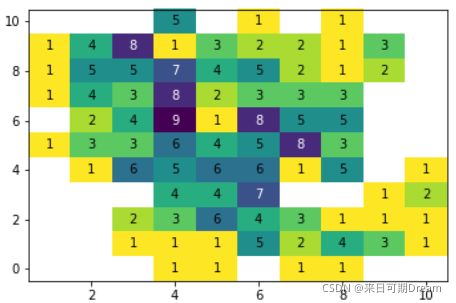
如果热图中有太多的单元格,注释将太多,无法看清。在这种情形下,建议不要添加注释,直接通过数据和色条传达信息。通常你会在单元格较少的分类热图中看到注释。实际上,seaborn 的 heatmap 函数中内置了一个添加注释的参数,稍后我们将讲解。
小提琴图:
我们可以通过几种方式绘制一个数值变量和一个分类变量之间的关系,表示为不同的抽象级别。小提琴图是较低级别的抽象。对于分类变量的每个类别,都会绘制数值变量的值分布情况。分布情况绘制为核密度估计,有点像平滑的直方图,关于核密度估计的讲解,可以参照上一章课程结尾的补充内容。
Seaborn 的 violinplot 函数可以创建将小提琴图和箱线图相结合的图表。
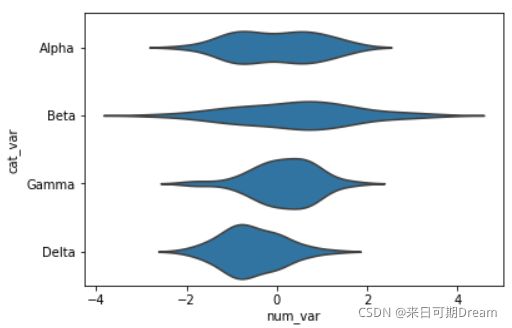
sb.violinplot(data = df, x = 'cat_var', y = 'num_var')
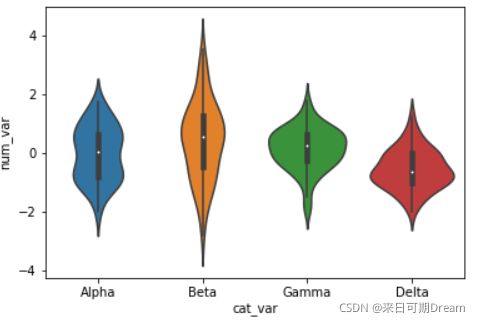
在此图中可以看出,数值数据在每个分类级别都具有不同的形状:Alpha 组呈双峰,Beta 组的变化范围相对更广,Gamma 组和 Delta 组分别呈负偏态和正偏态。还可以看出,每个级别都以不同的颜色呈现,就像上节课的普通 countplot 一样。如果没必要区分颜色,我们可以使用 “color” 参数使所有曲线的颜色都一样。
在每个曲线内,都有一个黑色的形状,其中包含一个白点。这就是上面提到的迷你箱线图,下个页面的课程将详细讨论箱线图。如果你想删除箱线图,可以在 violinplot 调用中设置 inner = None ,使最终的图表看起来更简单。
base_color = sb.color_palette()[0]
sb.violinplot(data = df, x = 'cat_var', y = 'num_var', color = base_color,
inner = None)

其他版本
就像横向条形图可以呈现为横条一样,小提琴图也可以水平呈现。Seaborn 很机智,可以根据是 “x” 还是 “y” 接受的分类变量来推断按照哪个屏幕方向绘制图表。但是如果两个变量都是数值(比如其中一个是离散型数值),则可以使用 “orient” 参数指定图表方向。
base_color = sb.color_palette()[0]
sb.violinplot(data = df, x = 'num_var', y = 'cat_var', color = base_color,
inner = None)
箱线图
箱线图(也被称为箱形图、盒须图等)是展示数值变量和分类变量之间关系的另一种方式。与小提琴图相比,箱线图更侧重于数据的汇总统计,主要报告每个分类级别数值的一组描述性统计量。可以使用 seaborn 的 boxplot 函数创建箱线图。
plt.figure(figsize = [10, 5])
base_color = sb.color_palette()[0]
# left plot: violin plot
plt.subplot(1, 2, 1)
ax1 = sb.violinplot(data = df, x = 'cat_var', y = 'num_var', color = base_color)
# right plot: box plot
plt.subplot(1, 2, 2)
sb.boxplot(data = df, x = 'cat_var', y = 'num_var', color = base_color)
plt.ylim(ax1.get_ylim()) # set y-axis limits to be same as left plot
注意,这里使用了 “color” 参数使每个箱子的颜色一样。为了更好地比较小提琴图和箱线图,我们在第二个图表上添加了 ylim 表达式,使两个图表的 y 轴范围相符。我们将 violinplot 返回的 Axes 对象分配给一个变量ax1,以编程方式获得范围值(ax1.get_ylim())。

小提琴图的内部方框和线条对应于箱线图的矩形箱子和须线。在箱线图中,箱子的中间线条表示分布的中位数,箱子的顶部和底部分别表示数据的第三个和第一个四分位数。因此,箱子的高度是四分位差(IQR)。箱子顶部的须线,表示从第三四分位数到最大值的范围,底部的须线表示从第一四分位数到最小值的范围。通常,须线长度会设置最大范围,默认情况下,设为 1.5 乘以 IQR。对于 Gamma 级别,底部须线下方有数据,表示在第一四分位数下方存在大于 1.5 倍 IQR 的单个离群值。
对比两个图表后发现,箱线图是比小提琴图更清晰的数据汇总。使用箱线图更容易比较不同组的统计值。如果你有很多组数据要比较,或者要构建解释性可视化,则箱线图更值得考虑。可以从箱线图中清晰地看出,Delta 组的中位数最低。另一方面,箱线图对数据分布的细节描绘没有小提琴图清晰:无法在 Alpha 级别的值中看到微弱的双峰性。小提琴图可能更适合探索数据,尤其因为 seaborn 还默认地在小提琴图中包含了箱线图。
其他版本
和 violinplot 一样,boxplot 也可以水平地呈现箱线图,将数字和分类特征设为相应的参数即可。
base_color = sb.color_palette()[0]
sb.boxplot(data = df, x = 'num_var', y = 'cat_var', color = base_color)

在 violinplot 中,除了默认的迷你箱线图之外,还有一个在小提琴图中绘制汇总统计信息的其他选项。通过设置 inner = 'quartile’,将在小提琴区域绘制三条虚线分别表示三个四分位数。虚线较粗的长横线表示中位数,位于两侧的短横线虚线表示第一四分位数和第三四分位数。
base_color = sb.color_palette()[0]
sb.violinplot(data = df, x = 'cat_var', y = 'num_var', color = base_color,
inner = 'quartile')