吴恩达《卷积神经网络》02——经典卷积网络

这一讲吴老师讲到的CNN模型包括：LeNet-5、AlexNet、VGG。此外还有ResNet（Residual Network，残差网络），以及 Inception Neural Network。

一、LeNet-5

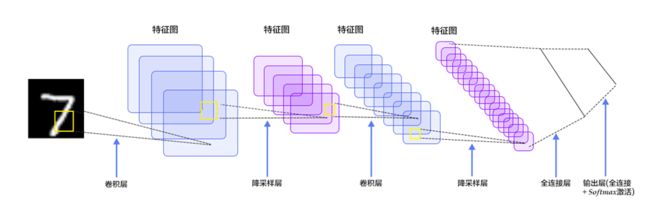
LeNet-5模型是Yann LeCun教授于1998年提出来的，它是第一个成功应用于数字识别问题的卷积神经网络。 在MNIST数据中，它的准确率达到大约99.2%。典型的LeNet-5结构包含CONV layer，POOL layer和FC layer，顺序一般是CONV layer->POOL layer->CONV layer->POOL layer->FC layer->FC layer->OUTPUT layer，即 y_hat。 下图所示的是一个数字识别的LeNet-5的模型结构：

该LeNet模型总共包含了大约6万个参数。 值得一提的是，当时Yann LeCun提出的LeNet-5模型池化层使用的是average pool，而且各层激活函数一般是Sigmoid和tanh。现在，我们可以根据需要，做出改进，使用max pool和激活函数ReLU。

该模型的特点有：

• LeNet-5 针对灰度图像而训练，因此输入图片的通道数为1。
• 该模型总共包含了6万个参数，远少于标准神经网络所需。
• 典型的 LeNet-5 结构包含卷积层（CONV layer），池化层（POOL layer）和全连接层（FC layer），排列顺序一般为 CONV layer->POOL layer->CONV layer->POOL layer->FC layer->FC layer->OUTPUT layer。一个或多个卷积层后面跟着一个池化层的模式至今仍十分常用。
• 当 LeNet-5模型被提出时，其池化层使用的是平均池化，而且各层激活函数一般选用 Sigmoid 和 tanh。现在，我们可以根据需要，做出改进，使用最大池化并选用 ReLU 作为激活函数。

相关论文：LeCun et.al., 1998. Gradient-based learning applied to document recognition。吴恩达老师建议精读第二段，泛读第三段。

二、AlexNet

AlexNet模型是由Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton共同提出的，其结构如下所示：

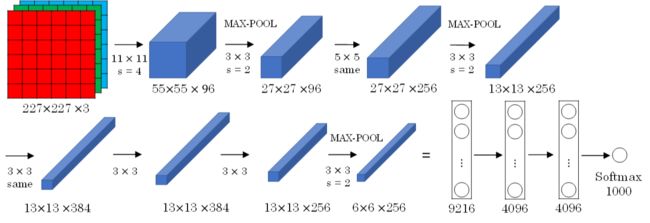
AlexNet模型与LeNet-5模型类似，只是要复杂一些，总共包含了大约6千万个参数。同样可以根据实际情况使用激活函数ReLU。原作者还提到了一种优化技巧，叫做Local Response Normalization(LRN)。 而在实际应用中，LRN的效果并不突出。

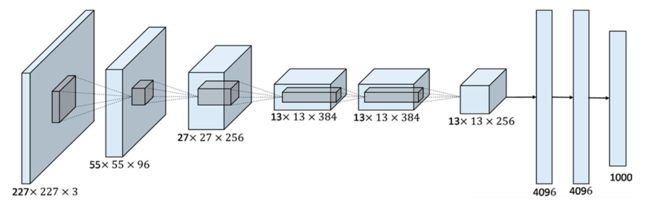
该模型的特点：

• 当用于训练图像和数据集时，AlexNet 能够处理非常相似的基本构造模块，这些模块往往包含大量的隐藏单元或数据。
• AlexNet模型使用了ReLu函数。

相关论文：Krizhevsky et al.,2012. ImageNet classification with deep convolutional neural networks。这是一篇易于理解并且影响巨大的论文，计算机视觉群体自此开始重视深度学习。

三、VGG-16

VGG-16模型更加复杂一些，一般情况下，其CONV layer和POOL layer设置如下：

• CONV = 3 × 3 filters，s = 1，same
• MAX-POOL = 2 × 2，s = 2

该模型的特点为：

• VGG-16，“16”指网络中包含16个卷积层和全连接层。
• 超参数较少，只需要专注于构建卷积层。
• 结构不复杂且规整，在每一组卷积层进行滤波器翻倍操作。
• VGG需要训练的特征数量巨大，包含多达1.38亿个参数。

VGG-16的结构如下所示：

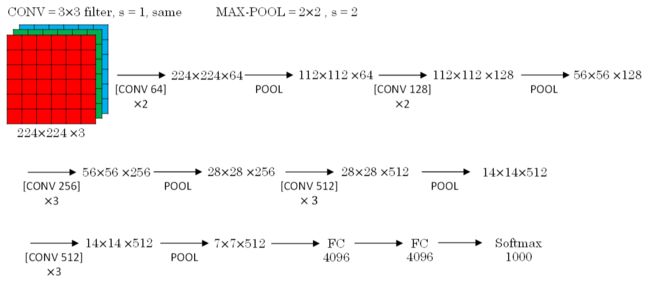
VGGNet探索了卷积神经网络深度与性能之间的关系，通过反复堆叠 3×3 的小型卷积核和 2×2 的最大池化层，成功地构筑了16~19层深度卷积神经网络。

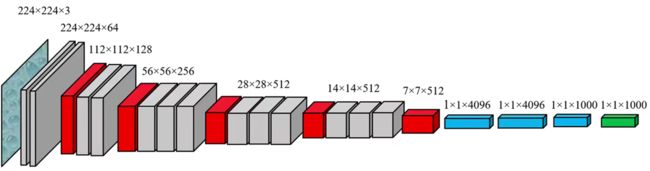
上图中，红色表示池化层，灰色表示卷积层，蓝色表示全连接层，最后通过softmax分类输出预测结果。由上图可以直观看出，feature map长宽的信息逐渐减小，通道的信息逐渐变多。

为什么在VGG中，用多个 3×3 的卷积核代替AlexNet中的 11× 11、7×7、5×5的卷积核？

如下图所示，对一个 5×5 大小的输入用 5×5 的卷积核做卷积会得到 Layer3 中的那个值。

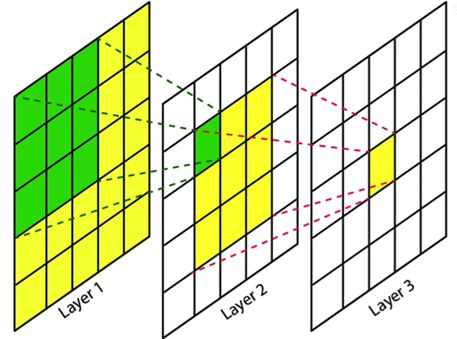
若对 5×5 的输入先用一个 3×3 的卷积核做卷积会得到如上图中 Layer2 的feature map，若对这个 3×3 的feature map使用一个 3×3 的卷积核做卷积也会得到 Layer3 中的那个值。

由此可以看出，做两次 3×3 卷积与一次 5×5 卷积得到的结果相同。那么我们就可以用2层 3×3 卷积替代一个 5×5 卷积。代替之后有很多好处：模型深度变深了，非线性次数变多了、学习能力变强了。且2层 3×3 卷积的参数（ 3×3×2×channels=18channels）是远远小于一个 5×5 卷积（ 5×5×1×channels=25channels）的。

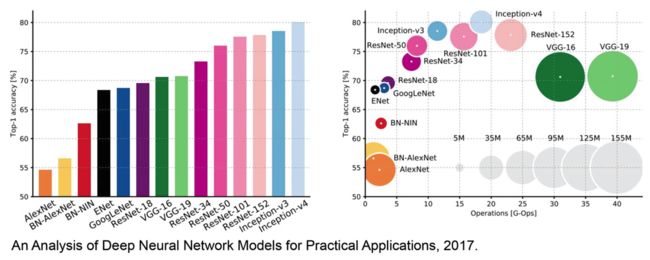
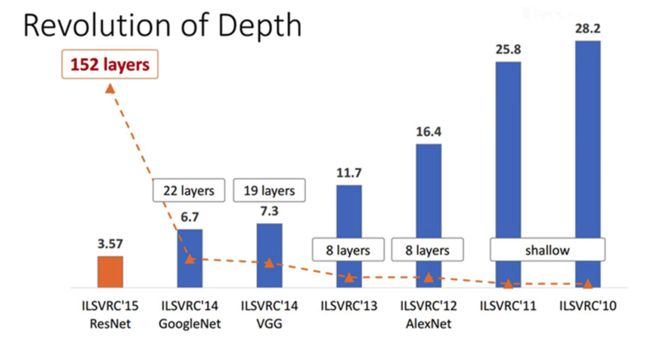
VGG模型深度仍不是很深，左边这个图可以看出它的准确率处于中等水平。右边这个图可以看出VGG的另一个特点：特别臃肿。计算量和参数量都很大。图中圆圈大小表示参数数量，圆圈越靠左表示模型准确度越高。VGG的参数多达1亿3千万。

四、ResNets

我们知道，如果神经网络层数越多，网络越深，源于梯度消失和梯度爆炸的影响，整个模型难以训练成功。解决的方法之一是人为地让神经网络某些层跳过下一层神经元的连接，隔层相连，弱化每层之间的强联系。 这种神经网络被称为Residual Networks(ResNets)。

Residual Networks由许多隔层相连的神经元子模块组成，我们称之为Residual block。单个Residual block的结构如下图所示：

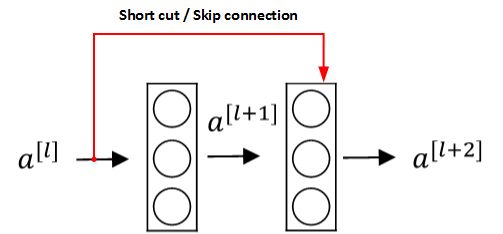
上面红色的部分就是skip connection，直接建立 $a$^$[l]$ 与 $a$^$[l+1]$ 之间的隔层联系。相应的表达式如下：
$z$^$[l+1]$ $=$ $W$^$[l+1]$$a$^$[l]$ $+$ $b$^$[l+1]$、 $a$^$[l+1]$ $=$ $g$($z$^$[l+1]$)、 $z$^$[l+2]$ $=$ $W$^$[l+2]$$a$^$[l+1]$ $+$ $b$^$[l+2]$、 $a$^$[l+2]$ $=$ $g$($z$^$[l+2]$ $+$ $a$^$[l]$)

$a$^$[l]$ 直接隔层与下一层的线性输出相连，与 $z$^$[l+2]$ 共同通过ReLu激活函数输出 $a$^$[l+2]$。

ResNets的提出使得卷积模型深度有了质的飞跃。

构建一个残差网络就是将许多残差块堆积在一起，形成一个深度网络。 该模型由Kaiming He, Xiangyu Zhang, Shaoqing Ren和Jian Sun共同提出。由多个Residual block组成的神经网络就是Residual Network。实验表明，这种模型结构对于训练非常深的神经网络，效果很好。其结构如下所示：

为了便于区分，在 ResNets 的论文He et al., 2015. Deep residual networks for image recognition中，非残差网络被称为普通网络（Plain Network）。将它变为残差网络的方法是加上所有的跳远连接。

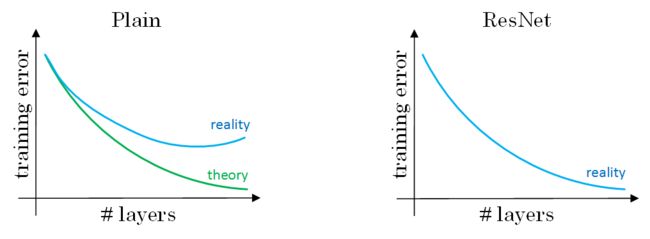
在理论上，随着网络深度的增加，性能应该越来越好。但实际上，对于一个普通网络，随着神经网络层数增加，训练错误会先减少，然后开始增多。但残差网络的训练效果显示，即使网络再深，其在训练集上的表现也会越来越好。

1. Why ResNets Work

下面用个例子来解释为什么ResNets能够训练更深层的神经网络。

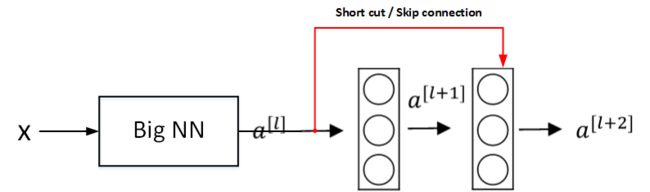
如上图所示，输入 $x$ 经过很多层神经网络后输出 $a$^$[l]$，$a$^$[l]$经过一个Residual block输出 $a$^$[l+2]$。$a$^$[l+2]$ 的表达式为：

$a$^$[l+2]$ $=$ $g$($z$^$[l+2]$ $+$ $a$^$[l]$) $=$ $g$($W$^$[l+2]$$a$^$[l+1]$ $+$ $b$^$[l+2]$ $+$ $a$^$[l]$)

输入 $x$ 经过Big NN后，若$W$^$[l+2]$ $\approx 0$, $b$^$[l+2]$ $\approx 0$, 则有$a$^$[l+2]$ $=$ $g$($a$^$[l]$) $=$ $ReLU$($a$^$[l]$) $=$ $a$^$[l]$ ($when$ $a$^$[l]$ $\ge 0$)

可以看出，即使发生了梯度消失，$W$^$[l+2]$ $\approx 0$, $b$^$[l+2]$ $\approx 0$，也能建立 $a$^$[l+2]$ 与 $a$^$[l]$的线性关系，且$a$^$[l+2]$ $=$ $a$^$[l]$，这其实就是identity function。$a$^$[l]$直接连到$a$^$[l+2]$，从效果来说，相当于直接忽略了$a$^$[l]$之后的这两层神经层。

这样，看似很深的神经网络，其实由于许多Residual blocks的存在，弱化削减了某些神经层之间的联系，实现隔层线性传递，而不是一味追求非线性关系，模型本身也就能“容忍”更深层的神经网络了。而且从性能上来说，这两层额外的Residual blocks也不会降低Big NN的性能。 而如果没有发生梯度消失时，训练得到的非线性关系会使得表现效果进一步提高。

注意，如果$a$^$[l]$ 与 $a$^$[l+2]$ 的维度不同，需要引入矩阵$W_s$ 与 $a$^$[l]$ 相乘，使得二者的维度相匹配。参数矩阵$W_s$ 既可以通过模型训练得到，也可以作为固定值，仅使 $a$^$[l]$ 截断或者补零。

上图是论文提供的 CNN 中 ResNet 的一个典型结构。卷积层通常使用 Same 卷积以保持维度相同，而不同类型层之间的连接（例如卷积层和池化层），如果维度不同，则需要引入矩阵 $W_s$ 。

五、Inception Network

1. 1x1 Convolutions

Min Lin, Qiang Chen等人提出了一种新的CNN结构，即1x1 Convolutions，也称Networks in Networks。这种结构的特点是滤波器算子filter的维度为1x1。对于单个filter，1x1的维度，意味着卷积操作等同于乘积操作。

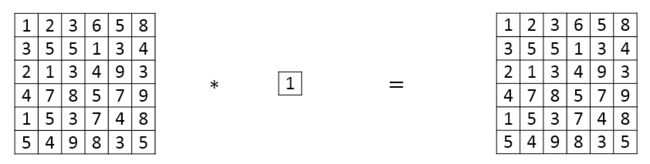
那么，对于多个filters，1x1 Convolutions的作用实际上类似全连接层的神经网络结构。效果等同于Plain Network中 $a$^$[l]$ 到 $a$^$[l+1]$ 的过程。这点还是比较好理解的。

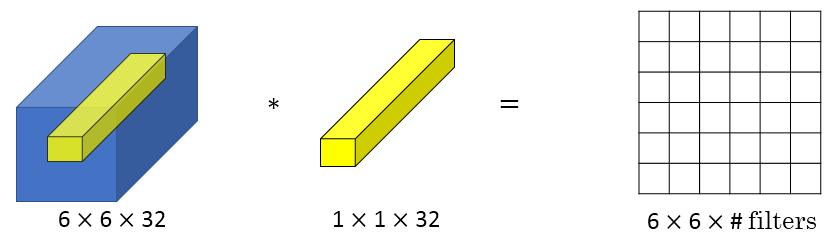
当通道数更多时，1x1 卷积的作用实际上类似全连接层的神经网络结构，从而降低（或升高，取决于滤波器组数）数据的维度。

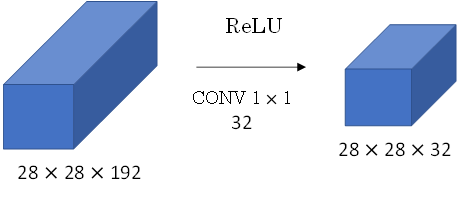
虽然论文Lin et al., 2013. Network in network中关于架构的详细内容并没有得到广泛应用，但是 1x1 卷积的理念十分有影响力，许多神经网络架构（包括 Inception 网络）都受到它的影响。

2. Inception Network Motivation

之前我们介绍的CNN单层的滤波算子filter尺寸是固定的，1x1或者3x3等。而Inception Network在单层网络上可以使用多个不同尺寸的filters，进行same convolutions，把各filter下得到的输出拼接起来。 除此之外，还可以将CONV layer与POOL layer混合，同时实现各种效果。但是要注意使用same pool。Inception 网络的作用即是代替人工来确定卷积层中的滤波器尺寸与类型，或者确定是否需要创建卷积层或池化层。

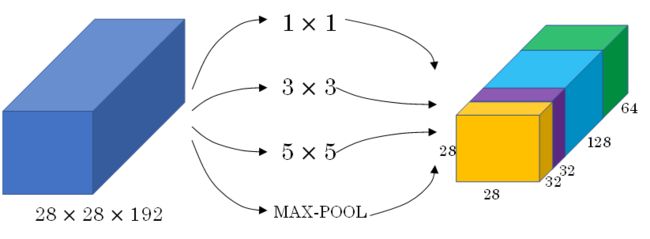
Inception Network由Christian Szegedy, Wei Liu等人提出。与其它只选择单一尺寸和功能的filter不同，Inception Network使用不同尺寸的filters并将CONV和POOL混合起来，将所有功能输出组合拼接，再由神经网络本身去学习参数并选择最好的模块。

相关论文：Szegedy et al., 2014, Going Deeper with Convolutions

3. 计算成本问题

Inception Network在提升性能的同时，会带来计算量大的问题。例如下面这个例子：

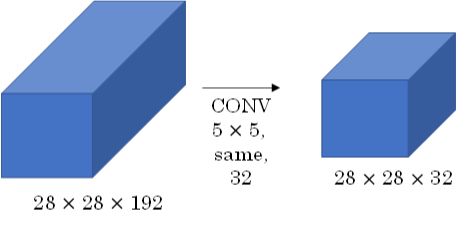
此CONV layer需要的计算量为：28x28x32x5x5x192=120m，其中m表示百万单位。可以看出但这一层的计算量都是很大的。为此，我们可以引入1x1 Convolutions来减少其计算量，结构如下图所示：

通常我们把该1x1 Convolution称为“瓶颈层”（bottleneck layer）。引入bottleneck layer之后，总共需要的计算量为：28x28x16x192+28x28x32x5x5x16=12.4m。明显地，虽然多引入了1x1 Convolution层，但是总共的计算量减少了近90%，效果还是非常明显的。由此可见，1x1 Convolutions还可以有效减少CONV layer的计算量。

4. Inception Network

上一节我们使用1x1 Convolution来减少Inception Network计算量大的问题。引入1x1 Convolution后的Inception module如下图所示：

多个Inception modules组成Inception Network，效果如下图所示：

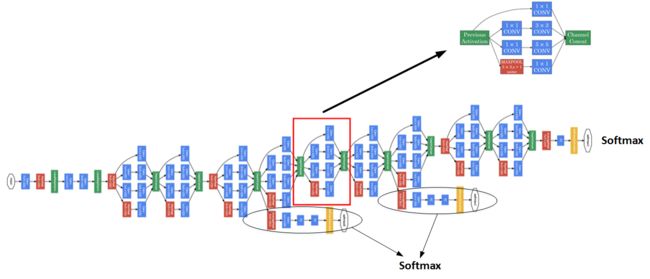
上述Inception Network除了由许多Inception modules组成之外，注意黑色椭圆圈出的隐藏层，这些分支都是 Softmax 的输出层，可以用来参与特征的计算及结果预测，起到调整并防止发生过拟合的效果。

经过研究者们的不断发展，Inception 模型的 V2、V3、V4 以及引入残差网络的版本被提出，这些变体都基于 Inception V1 版本的基础思想上。顺便一提，Inception 模型的名字来自电影《盗梦空间》。

六、其他

1. 使用开源的实现方案

很多神经网络复杂细致，并充斥着参数调节的细节问题，因而很难仅通过阅读论文来重现他人的成果。想要搭建一个同样的神经网络，查看开源的实现方案会快很多。

GitHub是一个面向开源及私有软件项目的托管平台，上面包含有许多优秀的CNN开源项目。关于GitHub具体内容不再介绍，有兴趣的小伙伴自行查阅。

2. 迁移学习（Transfer Learning）

有关Transfer Learning的相关内容，我们在 Coursera吴恩达《构建机器学习项目》课程笔记– 机器学习策略（下）中已经详细介绍过，这里就不再赘述了。

计算机视觉是一个经常用到迁移学习的领域。在搭建计算机视觉的应用时，相比于从头训练权重，下载别人已经训练好的网络结构的权重，用其做预训练，然后转换到自己感兴趣的任务上，有助于加速开发。

对于已训练好的卷积神经网络，可以将所有层都看作是冻结的，只需要训练与你的 Softmax 层有关的参数即可。 大多数深度学习框架都允许用户指定是否训练特定层的权重。

而冻结的层由于不需要改变和训练，可以看作一个固定函数。可以将这个固定函数存入硬盘，以便后续使用，而不必每次再使用训练集进行训练了。

上述的做法适用于你只有一个较小的数据集。 如果你有一个更大的数据集，应该冻结更少的层，然后训练后面的层。越多的数据意味着冻结越少的层，训练更多的层。如果有一个极大的数据集，你可以将开源的网络和它的权重整个当作初始化（代替随机初始化），然后训练整个网络。

3. 数据增强（Data Augmentation）

计算机视觉领域的应用都需要大量的数据。当数据不够时，数据增强（Data Augmentation）就有帮助。常用的数据扩增包括镜像翻转、随机裁剪、色彩转换。

常用的Data Augmentation方法是对已有的样本集进行Mirroring和Random Cropping。

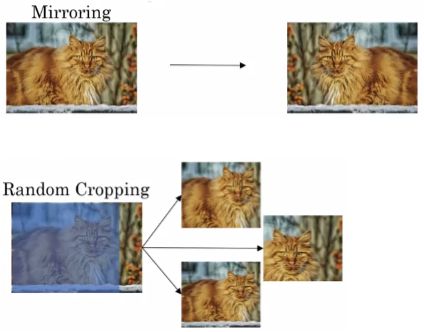
另一种Data Augmentation的方法是color shifting。color shifting就是对图片的RGB通道数值进行随意增加或者减少，改变图片色调。

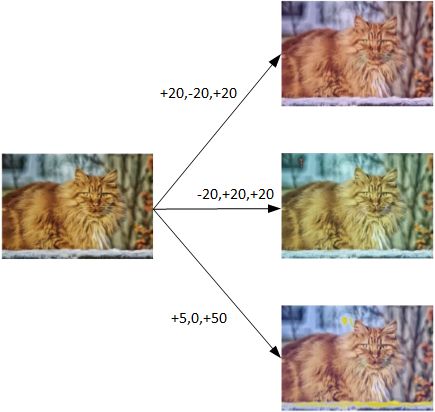
除了随意改变RGB通道数值外，还可以更有针对性地对图片的RGB通道进行PCA color augmentation，也就是对图片颜色进行主成分分析，对主要的通道颜色进行增加或减少，可以采用高斯扰动做法。 这样也能增加有效的样本数量。具体的PCA color augmentation做法可以查阅AlexNet的相关论文。

最后提一下，在构建大型神经网络的时候，data augmentation和training可以由两个不同的线程来进行。

4. 计算机视觉现状（State of Computer Vision）

通常，学习算法有两种知识来源：

• 被标记的数据
• 手工工程

手工工程（Hand-engineering，又称 hacks） 指精心设计的特性、网络体系结构或是系统的其他组件。手工工程是一项非常重要也比较困难的工作。在数据量不多的情况下，手工工程是获得良好表现的最佳方式。 正因为数据量不能满足需要，历史上计算机视觉领域更多地依赖于手工工程。近几年数据量急剧增加，因此手工工程量大幅减少。

神经网络需要数据，不同的网络模型所需的数据量是不同的。 Object dection，Image recognition，Speech recognition所需的数据量依次增加。一般来说，如果data较少，那么就需要更多的hand-engineering，对已有data进行处理，比如上一节介绍的data augmentation。模型算法也会相对要复杂一些。如果data很多，可以构建深层神经网络，不需要太多的hand-engineering，模型算法也就相对简单一些。

值得一提的是hand-engineering是一项非常重要也比较困难的工作。很多时候，hand-engineering对模型训练效果影响很大，特别是在数据量不多的情况下。

另外，在模型研究或者竞赛方面，有一些方法能够有助于提升神经网络模型的性能：

• 集成（Ensembling）：独立地训练几个神经网络，并平均输出它们的输出。
• Multi-crop at test time：将数据扩增应用到测试集，对结果进行平均。

但是由于这些方法计算和内存成本较大，一般不适用于构建实际的生产项目。

参考文章：Coursera吴恩达《卷积神经网络》课程笔记（2）-- 深度卷积模型：案例研究