文献阅读——神经网络剪枝技术（二）

神经网络剪枝技术

1.神经网络压缩技术

当前的神经网络压缩技术主要有6类：网络剪枝、参数共享、量化、网络分解、网络蒸馏、紧凑网络设计。
1.1网络剪枝
网络剪枝使用的比较广泛，将会在第二节详细介绍进行介绍。
1.2参数共享
主要思想是让网络中多个参数共享同一值，但具体实现方式不同。如利用k均值聚类、低秩分解、权重采样等。但可能会因为过分追求模型压缩比导致模型精度的下降。
1.3量化
量化方法通过降低权重所需要的比特数来压缩原始网络，主要包括低精度和重编码两类方法。如低精度方法使用更低位数的浮点数或整型数表示权重参数进行训练、测试或存储；重编码则是对原始数据进行重编码，采用更少的位数对原有数据进行表示，代表有二值化权重/二值化神经网络。
目前对于图像分类许多量化技术都可达到无损压缩；但进行较为复杂的如分割任务时使用量化通常会对模型精度带来巨大影响。
1.4网络分解
网络分解主要将矩阵二维张量进行奇异值分解，推广到三维卷积核使用多个一维张量外积求和逼近来减少网络推断的时间。
1.5网络蒸馏
网络蒸馏又叫知识蒸馏，目的是将教师模型学到的知识转化到学生模型中。比如将教师模型的softmax层作为学生模型的监督；但有些任务中直接使用教师模型的输出对学生模型进行监督会比较困难，因此可参考将教师模型的中间层输出作为对学生模型的中级监督信息等。
知识蒸馏目前主要应用在分类任务中，对更加复杂的检测、分割任务还应用的较少；而且学生模型的设计缺少重要指导信息会导致学生模型较难训练成功。这些都导致知识蒸馏方法还无法成为模型压缩的主流方法。
1.6紧凑网络设计
前述方法主要对已训练好的网络进行压缩，紧凑网络设计则旨在设计更加精简有效的网络。大致分为两大方向：紧凑卷积结构和网络结构搜索。
紧凑卷积结构：SqueezeNet,MobileNet，ShffleNet等轻量级网络系列，致力于设计出更加精简有效的网络；
网络结构搜索：Neural Architecture Search,NAS神经网络结构搜索的不同之处在于，传统的网络模型及参数均为人工设计，往往导致设计出的模型并非最优。NAS则通过搜索方法寻找最优的神经网络架构，一旦此类方法成熟，将很适合工业界应用；但目前NAS还有待发展，使用神经网络结构搜索需要很大的硬件和时间消耗。如何使用更少的资源、花费更少的时间来搜索出想要的网络是今后的重要目标

2.神经网络剪枝技术

神经网络剪枝技术是神经网络压缩技术的一个子领域。依据剪枝粒度可分为非结构化剪枝和结构化剪枝，涉及到一个关键问题就是如何度量网络中连接的冗余性。
目前依据实现大致分为基于度量标准、基于重建误差、基于硬件部署的剪枝，并有逐渐向AutoML发展的趋势。本节主要从实现方法进行展开，对近年来的经典剪枝算法进行梳理。
2.1基于度量标准的剪枝
基于度量标准的剪枝算法通常聚焦于提出判断神经元是否重要的度量标准，根据此标准将“不重要”的神经元或过滤器进行剪枝。根据裁剪的对象不同，可分为对单个神经元进行非结构化剪枝和对滤波器操作的结构化剪枝；根据度量对象不同，可分为基于权重、基于激活率、基于梯度的度量标准。
2.1.1 基于权重的度量标准
如文献[1]基于权重参数的大小进行连接冗余性的判断，从而减小神经网络计算和存储的复杂程度。主要方法包含三步：初始阶段通过正常的网络学习连接，随后将所有权重低于阈值的“不重要”的连接删除进行非结构化剪枝，第二阶段重新训练系数化网络，以便剩余的连接可以补偿被裁剪的连接从而恢复模型精度。最终本文在不影响准确率的情况下将AlexNet参数量减小了9x，VGG-16的参数量减小了13x。

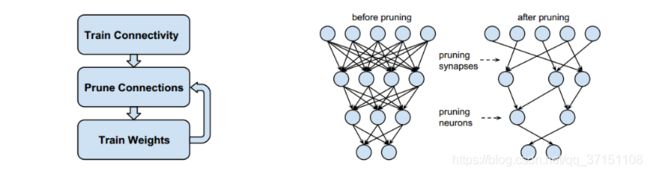
图2.1 基于权重的非结构化剪枝

文献[2]提出的基于几何中心的滤波器评价指标（FPGM）则根据卷积核的相似性而不是“重要性”作为剪枝的度量标准。本文将滤波器抽象成欧式空间内的点，通过计算神经网络中每一层滤波器与该层滤波器空间的几何中心的欧氏距离判断滤波器间信息的重合程度。因为较高的相似性意味着更高的可替代性，因此将该部分冗余的滤波器进行剪枝达到压缩网络的目的。与通过网络修剪权重相比，过滤器修剪是一种自然结构化的修剪方式，不会引入稀疏性，因此不需要使用稀疏库或任何专用硬件。另一方面，由于FPGM算法考虑到了同层滤波器之间的关系，取得了较好的剪枝效果，最终在CIFAR-10数据集上，将ResNet-110的FLOPs降低了52%，在ImageNet数据集上降低了42%的计算量。

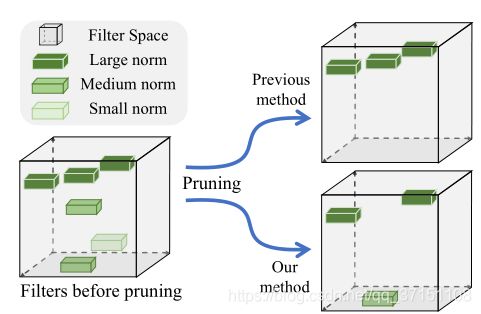
图2.2 基于权重的结构化剪枝

2.1.2 基于激活率的度量标准
另一种度量方式是将网络中激活的比例作为度量依据，如文献[3]中认为大部分激活值趋于0的神经元都是冗余的，剔除该部分神经元可大大降低模型的大小和运算量而不会影响模型精度。因此文章提出将激活值中0的平均占比（APoZ,Average Percentagr of Zeros）作为衡量滤波器重要性的度量标准。最终在MNIST数据集上，LeNet参数量压缩至原始的1/3，在ImageNet数据集中VGG-16的参数压缩比为2.59x。
文献[4]则利用信息熵作为是否剪枝的度量，通过计算各通道熵值大小并从大到小排列后，根据设定阈值进行剪枝，得到压缩后的网络模型。最终在ImageNet数据集上使用VGG-16网络获得了3.3x的加速比和16.64x的压缩比；ResNet-50网络获得了1.54x的加速比和1.47x的压缩比。

（a）剪枝前

（b）剪枝后
图2.3 基于激活率的非结构化剪枝

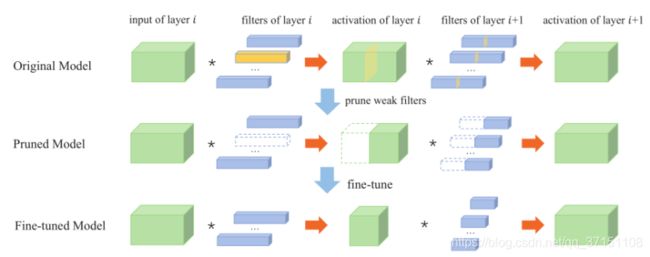
图2.4 基于激活率的结构化剪枝

2.1.3 基于梯度的度量标准
基于梯度的度量标准通常从损失函数出发寻找出对网络性能影响最小的神经元，相关工作于上世纪90年代就已开展。如LeCun等人提出的OBD算法将损失函数相对权重的二阶导数作为评判依据，将部分神经元进行裁剪；文献[5]的ORACLE方法将剪枝转化为优化问题，即通过一定阶数的泰勒展开近似剪枝前后损失函数的变化从而每次迭代可去除部分特征映射导致的损失变化。最终在ImageNet数据集上对VGG-16t网络获得了2.5x的加速比。
文献[6]同样将损失函数对权重参数的梯度作为显著性连接的评判标准，从而对网络进行非结构性剪枝，最终AlexNet、VGG-16在CIFAR-10数据集上进行了测试，分别得到了10.5x、19.1x的压缩比。
2.2基于重建误差的剪枝
基于重建误差的剪枝算法致力于寻找原始输入的子集，若原始输入的部分子集即可达到同原始输入同样的重建效果，则可将冗余部分进行剪枝，从而将网络剪枝转化为输出特征重建误差的优化问题。
文献[7]基于提出的NISP算法（Neuron Importance Score Propagation）应用特征排序技术度量FRL层中每个神经元的重要性，并在确保该层重建误差最小的基础上按照设定的裁剪率完成低传播特性神经元的裁剪。NISP算法将神经元的裁剪巧妙地转变为原始网络与剪枝网络响应之间的差异最小化问题。在ImageNet数据集使用AlexNet降低了67.85%的FLOPs,ResNet56降低了43.61%的FLOPs。
文献[8]基于贪心策略搜索输入子图代替原始输入，通过计算子图产生的输出逼近原始输出，将滤波器的筛选通过重建误差的优化完成，从而保证剪枝后网络结构不发生改变，但拥有较少的滤波器和通道数。最终在ResNet50减少了2.26x的FLOPs和2.06x的压缩比，在VGG-16减少了3.31x的FLOPs和16.63x的压缩比并在少样本数据集CUB-200及Indoor-67中取得了良好的迁移效果。

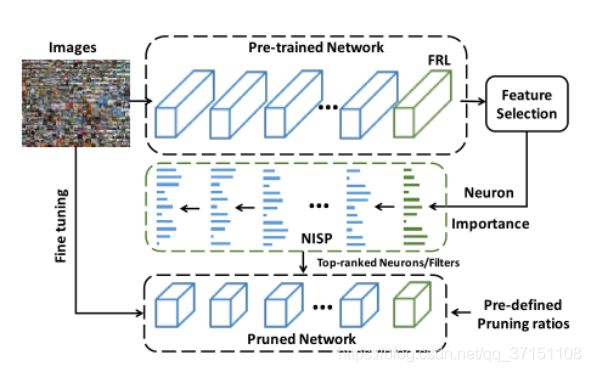
图2.5 基于重建误差的非结构化剪枝

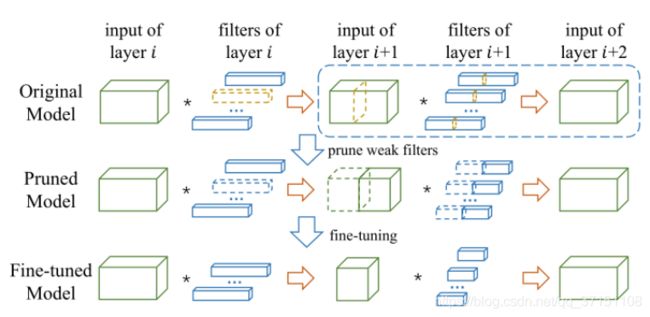
图2.6 基于重建误差的结构化剪枝

2.3基于硬件部署的剪枝
稀疏化网络由于其irregular的访问模式不便于神经网络的硬件实现，也无法从能量利用率上最大限度的裁剪模型为此考虑到实际硬件部署的便利性，也有研究人员进行了一系列探索。如文献[9]利用神经网络每层的能耗决定剪枝的顺序。通过计算神经网络的计算能耗及数据转移能耗，对能耗较大的层次（主要为卷积层）分配更高的裁剪优先级；进一步对于需要裁剪的层次，基于权重的度量标准进行裁剪，从而能够最大限度的降低模型能耗。通过最终将AlexNet和GooLeNet的能耗分别降低了3.7x及1.6x。
文献[10]提出的NetAdapt则以自动优化的方式降低网络的资源消耗，从而满足神经网络应用于移动平台的实际需求，同时最大化精度。NetAdapt的优化策略共有3部分：首先根据实际资源预算（如时延）进行直接度量，随后根据“资源减少策略”选择一定数量的滤波器或特征映射进行删除，并对剪枝后的网络进行微调以恢复精度。最后一旦达到目标预算，网络将再次微调，直至收敛。NetAdapt的有效性在于其在移动CPU和移动GPU上都能对精度和时延进行有效权衡，如对于ImageNet分类任务，NetAdapt在MobileNet-V1上实现了1.7x的推断加速。

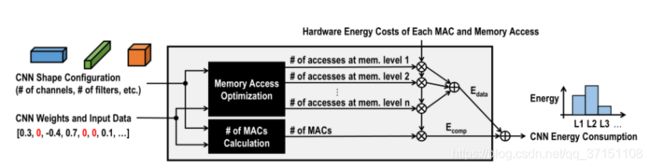
图2.7 基于能耗度量的结构化剪枝

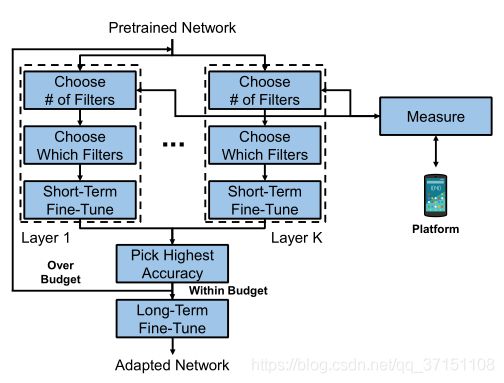
图2.8 基于应用预算度量的结构化剪枝

参考文献

[1]Han, Song & Pool, Jeff & Tran, John & Dally, William. (2015). Learning both Weights and Connections for Efficient Neural Networks. an, Song, Pool, Jeff, Tran, John, and Dally, William J. Learning both weights and connections for efficient neural networks. In Advances in Neural Information Processing Systems, 2015.
[2]He, Yang & Liu, Ping & Wang, Ziwei & Hu, Zhilan & Yang, Yi. (2019). Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration. 4335-4344. 10.1109/CVPR.2019.00447.
[3]Hu, Hengyuan & Peng, Rui & Tai, Yu-Wing & Tang, Chi-Keung. (2016). Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures.
[4]Luo, Jian-Hao & Wu, Jianxin. (2017). An Entropy-based Pruning Method for CNN Compression.
[5]Molchanov, Pavlo & Tyree, Stephen & Karras, Tero & Aila, Timo & Kautz, Jan. (2016). Pruning Convolutional Neural Networks for Resource Efficient Transfer Learning.
[6]Lee, Namhoon & Ajanthan, Thalaiyasingam & Torr, Philip. (2018). SNIP: Single-shot Network Pruning based on Connection Sensitivity.
[7]Yu, Ruichi & Li, Ang & Chen, Chun-Fu & Lai, Jui-Hsin & Morariu, Vlad & Han, Xintong & Gao, Mingfei & Lin, Ching-Yung & Davis, Larry. (2018). NISP: Pruning Networks Using Neuron Importance Score Propagation. 9194-9203. 10.1109/CVPR.2018.00958.
[8]Luo, Jian-Hao & Wu, Jianxin & Lin, Weiyao. (2017). ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression. 5068-5076. 10.1109/ICCV.2017.541.
[9]Yang, Tien-Ju & Chen, Yu-Hsin & Sze, Vivienne. (2017). Designing Energy-Efficient Convolutional Neural Networks Using Energy-Aware Pruning. 6071-6079. 10.1109/CVPR.2017.643.
[10] Yang, Tien-Ju & Howard, Andrew & Chen, Bo & Zhang, Xiao & Go, Alec & Sze, Vivienne & Adam, Hartwig. (2018). NetAdapt: Platform-Aware Neural Network Adaptation for Mobile Applications.