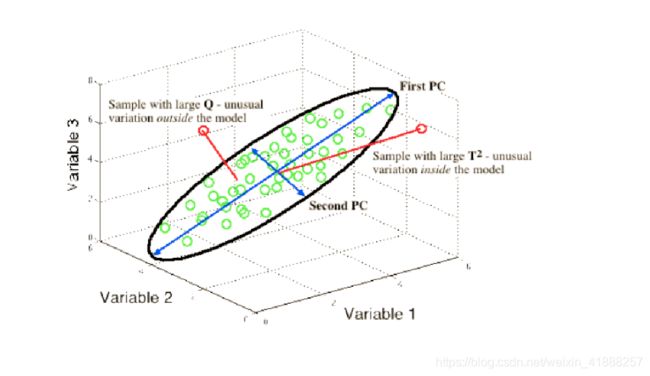
主成分分析（PCA）原理与故障诊断（SPE、T^2以及结合二者的综合指标）- Python实现

Python 代码

import numpy as np
from scipy.stats import norm, chi2
from scipy import stats
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

#生成正常数据
num_sample=100
a = 10*np.random.randn(num_sample, 1)
x1 = a + np.random.randn(num_sample, 1)
x2 = 1*np.sin(a) + np.random.randn(num_sample, 1)
x3 = 5*np.cos(5*a) +np.random.randn(num_sample, 1)
x4 = 0.8*x2 + 0.1*x3+np.random.randn(num_sample, 1)
x = np.c_[x1,x2,x3,x4]
xx_train=x

#产生测试集
a = 10*np.random.randn(num_sample, 1)
x1 = a + np.random.randn(num_sample, 1)
x2 = 1*np.sin(a) + np.random.randn(num_sample, 1)
x3 = 5*np.cos(5*a) +np.random.randn(num_sample, 1)
x4 = 0.8*x2 + 0.1*x3+np.random.randn(num_sample, 1)
xx_test = np.c_[x1,x2,x3,x4]
xx_test[50:,1]=xx_test[50:,1]+15

Xtrain =xx_train
Xtest =xx_test


def pca(data):
    data_mean = np.mean(data,0)
    data_std = np.std(data,0)
    data_nor = (data - data_mean)/data_std
    X = np.cov(data_nor.T)
    P,v,P_t = np.linalg.svd(X)  #载荷矩阵计算  此函数返回三个值 u s v 此时v是u的转置
    Z = np.dot(P,P_t)
    v_sum = np.sum(v)
    k = []##主元个数
    print("len(v):", len(v))
    print("v:",  v)
    for x in range(len(v)):
        PE_k = v[x]/v_sum
        if x == 0:
            PE_sum = PE_k
        else:
            PE_sum = PE_sum + PE_k
        if PE_sum < 0.85:   #累积方差贡献率
            pass
        else:
            k.append(x+1)
            print("k:", k)
            break
    ###################################################################
    # raw_pca = PCA(n_components=4)
    # train_data_decom = raw_pca.fit_transform(data_nor)
    # explained_variance = raw_pca.explained_variance_
    # raw_P = raw_pca.components_.T
    # print("explained_variance:", explained_variance)
    # print("raw_P:", raw_P)
    ##################################################################

    n_components = k[0]  # 2

    print("P:", P)

    ##新主元
    p_k = P[:,:n_components]
    v_I = np.diag(1/v[:n_components])

    confidence = 0.99
    ##T统计量阈值计算
    coe = n_components*(np.shape(data)[0]-1)*(np.shape(data)[0]+1)/((np.shape(data)[0]-n_components)*np.shape(data)[0])

    t_limit = coe*stats.f.ppf(confidence,n_components,(np.shape(data)[0]-n_components))
    print("t_limit:", t_limit)
    
    ##SPE统计量阈值计算
    theta1 = np.sum((v[n_components:])**1)
    theta2 = np.sum((v[n_components:])**2)
    theta3 = np.sum((v[n_components:])**3)
    h0 = 1 - (2 * theta1 * theta3) / (3 * (theta2 ** 2))

    c_alpha = norm.ppf(confidence)

    spe_limit = theta1 * ((h0 * c_alpha * ((2 * theta2) ** 0.5) / theta1 + 1 + theta2 * h0 * (h0-1) / (theta1 ** 2)) ** (1 / h0))

    print("spe_limit:", spe_limit)
    return v_I, p_k, data_mean, data_std, t_limit, spe_limit,v,P,k

#计算T统计量
def T2(data_in, data_mean, data_std, p_k, v_I):
    test_data_nor = ((data_in - data_mean)/data_std).reshape(len(data_in),1)
    T_count = np.dot(np.dot((np.dot((np.dot(test_data_nor.T,p_k)), v_I)), p_k.T),test_data_nor)
    return T_count
 #计算SPE统计量
def SPE(data_in, data_mean, data_std, p_k):
    test_data_nor = ((data_in - data_mean)/data_std).reshape(len(data_in),1)
    I = np.eye(len(data_in))
    Q_count = np.dot(np.dot((I - np.dot(p_k, p_k.T)), test_data_nor).T,np.dot((I - np.dot(p_k, p_k.T)), test_data_nor))
    #Q_count = np.linalg.norm(np.dot((I - np.dot(p_k, p_k.T)), test_data_nor), ord=None, axis=None, keepdims=False)
    return Q_count



if __name__ == "__main__":
    v_I, p_k, data_mean, data_std, t_limit, spe_limit,v,P,k = pca(Xtrain)
    # 循环计算
    test_data = Xtest
    t_total = []
    q_total = []
    for x in range(np.shape(test_data)[0]):
        data_in = Xtest[x, :]
        t = T2(data_in, data_mean, data_std, p_k, v_I)
        q = SPE(data_in, data_mean, data_std, p_k)
        t_total.append(t[0, 0])
        q_total.append(q[0, 0])

    ##画图
    plt.figure(figsize=(16, 9))
    ax1 = plt.subplot(2, 1, 1)
    plt.plot(t_total)
    plt.plot(np.ones((len(test_data))) * t_limit, 'r*', label='99% $T^2$ control limit')
    plt.axhline(y=t_limit)
    ax1.set_ylim(0, 100)
    plt.xlim(0, 100)
    ax1.set_xlabel(u'Samples')
    ax1.set_ylabel(u'Hotelling statistic')
    plt.legend()

    ax1 = plt.subplot(2, 1, 2)
    plt.plot(q_total)
    plt.plot(np.ones((len(test_data))) * spe_limit, 'r', label='99% Q control limit')
    ax1.set_ylim(0, 30)
    plt.xlim(0, 100)
    ax1.set_xlabel(u'Samples')
    ax1.set_ylabel(u'SPE(Q)')
    plt.legend()
    plt.show()

关于 np.linalg.svd() 函数，详见 numpy.linalg.svd函数

参考：

1. 主成分分析（PCA）原理与故障诊断（SPE、T^2以及结合二者的综合指标）-MATLAB实现
2. 百度文库 基于pca的故障诊断
3. 百度文库 多变量统计故障诊断方法
4. 百度文库 PCA故障诊断步骤
5. 基于PCA的线性监督分类的故障诊断方法-T2与SPE统计量的计算
6. 百度文库 大作业基于PCA故障诊断
7. 基于PCA的故障诊断方法1
8. Python 完整代码 主成分分析（PCA）过程监测和故障识别-----Python实现
9. 核主成分分析（Kernel PCA, KPCA）的MATLAB 实现
   10.github完整代码