第十二届蓝桥杯B组省赛真题题解与考点总结
前言
第12届蓝桥杯也是我第一次参加的蓝桥杯比赛,当时做的其实挺差的,水平有限也补不了题,时隔一年为了准备第13届蓝桥杯,打算把近几年的蓝桥杯真题给补了,但是找遍全网发现也没有一个相对完整的题解,于是就产生了自己动手写题解的想法。
试题A:空间
考点
计算机常识,计算机常识也是第一次出现在蓝桥杯的填空题当中,这在往年是没有的,往年第一题通常是一道简易的签到题。
答案:67108864
题解
1MB=1024KB 1KB=1024B 1B=8位
所以存放32位元素可以存放 256 * 1024 * 1024 * 8 / 32
试题B:卡片
考点
数位截取,数位截取可以说是基本中的基本了,蓝桥杯也多次考察属于是必须掌握的内容。这里还需要注意的是填空题与平时acm题不一样相当于没有输入的自测,所以需要把数据先处理到程序当中。
答案:3181
题解
先看数据范围,总共的牌才2e4那么暴力做即可,从1开始制作,将每个数字上的每一位提取然后减去一张相应的数字的牌如果小于0说明说制作失败。
#include试题C:直线
考点
暴力枚举、STL、精度问题、几何
第一次参赛的时候没有想出来怎么做,主要是那时候还不怎么会STL,现在看来还是挺简单的,但是有个精度问题卡了很多人。
答案:40257
题解
解法1
两点确定一条直线 当直线斜率存在时,我们记该直线为 y = k x + b y=kx+b y=kx+b其中 k = ( y 2 − y 1 ) / ( x 2 − x 1 ) , b = y 2 − k ∗ x 2 k=(y2-y1)/(x2-x1),b=y2-k*x2 k=(y2−y1)/(x2−x1),b=y2−k∗x2这里需要注意一下b可能会因为精度问题造成答案错误(出现double除法时常常会出现一些问题),所以将b的形式转换为 b = ( y 2 ∗ ( x 2 − x 1 ) − ( y 2 − y 1 ) ∗ x 2 ) / ( x 2 − x 1 ) ( 两 点 式 ) b=(y2*(x2-x1)-(y2-y1)*x2)/(x2-x1)(两点式) b=(y2∗(x2−x1)−(y2−y1)∗x2)/(x2−x1)(两点式)然后加上斜率不存在的和等于0的41条直线即可。
#include解法2
我们可以将直线转为更一般的形式 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0这样可以避免讨论斜率存在与否,其中 由 两 点 式 可 知 ( y − y 1 ) / ( y 2 − y 1 ) = ( x − x 1 ) / ( x 2 − x 1 ) 化 简 合 并 同 类 项 可 得 ( y 1 − y 2 ) x + ( x 2 − x 1 ) y − y 1 ( x 2 − x 1 ) + x 1 ( y 2 − y 1 ) 由两点式可知(y-y1)/(y2-y1)=(x-x1)/(x2-x1)化简合并同类项可得(y1-y2)x+(x2-x1)y-y1(x2-x1)+x1(y2-y1) 由两点式可知(y−y1)/(y2−y1)=(x−x1)/(x2−x1)化简合并同类项可得(y1−y2)x+(x2−x1)y−y1(x2−x1)+x1(y2−y1)同样用set来存储这三个系数,注意着三个系数需要同时除以他们的公约数以保证是不同的直线。
#include试题D:货物摆放
考点
约数、循环优化
答案:2430
题解
最暴力的三重循环时间复杂度为O(n3)n的大小为1e16显然会超时,进一步优化可以只枚举两个参数判断n和第三个参数的关系L==n/(W*H),还是超时。进一步思考 L ∗ W ∗ H = n L*W*H=n L∗W∗H=n那么L、W、H自然是n的约数,那么我们把所有的约数都求出来看看有多少个看看是否能降低问题的规模,由于是填空题可以选择打表出所有的约数,所以求一个数的约数使用暴力的方法O(n1/2)你会发现只有128个,那么我们再用枚举两个参数的方法很容易就可以得到答案。
#include
//cout<
int ans=0;
for(int i=1;i<=cnt;i++){
for(int j=1;j<=cnt;j++){
if(n%(yue[i]*yue[j])==0)
ans++;
}
}
cout<<ans;
return 0;
}
试题E:路径
考点
最短路径、最小公倍数、最小公约数
前面两道题都没有做出来,这道压轴居然做出来了,我觉得上面两个难度都比这一个大,不是很懂为什么会放在压轴。
答案:10266837
题解:
最短路的板子题,根据题目要求建好图,任意使用一个最短路算法即可得到答案,就算使用复杂度最大的floyd,大约10s也可以得到答案。
#include试题F:时间显示
考点
模拟,时间进制转换
时间真是蓝桥杯最爱考的考点了,平年闰年啥的需要掌握
题解
观察一下数据范围,直接进行进制转换即可
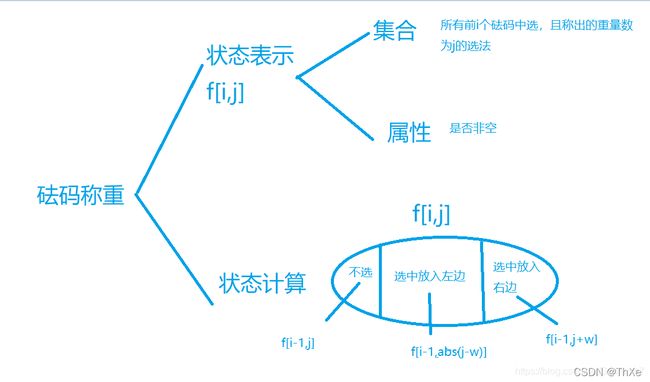
#include试题G:砝码称重
考点
DP动态规划、DFS(骗分)
参赛时直接看傻,这道题啥也没写,现在看来dp估计还是想不出来但是骗分还是有机会的。
题解
解法1 DFS(50%)
思路就能称的重量一定是砝码重的一边减去轻的一边,一开始天平为空,每次砝码可以放左边或者放在右边,直接深度优先搜索跑一遍用set统计答案即可。
#include解法2
一般来说能够深搜的题且是求方案数的都可以用DP来优化,这题就是最好的例证。(引用y总的图)
#include试题H:杨辉三角形
考点
组合数学、找规律、二分
题解
暴力做相信大家都会,用二维数组模拟即可。但是要拿到所有分首先你要知道杨辉三角与组合数学的关系,然后再来找规律,具体用代码来解释吧
#include 试题I:双向排序
考点
排序(骗分)、思维、线段树、平衡树
题解
解法1
sort模拟骗分,按照题意模拟即可大概能拿50%的分数
解法2
线段树合并
解法3
思维+栈
试题J:括号序列
考点:
DP
题解:
首先先要知道括号序列的一些性质:
(1) 左、右括号的总数量相等
(2) 任意前缀的左括号数量必须大于等于右括号数量
(3) 为了尽可能添加少的括号,所以添加的左、右括号不会出现如同“()”的形式,添加一对对应括号,那么删除掉这一对括号依然是合法序列且长度变短,所以添加的左括号一定是与原序列的一个右括号对应,同理添加的右括号与原序列的左括号对应。
添加括号的最小值: 从前往后遍历,当前前缀中,若左括号的数量小于右括号的数量,则需要添加对应数量的左括号,若遍历结束后左括号数量大于右括号,则需要添加对应数量的右括号。
添加括号的方案:
(1)左括号与右括号添加的位置方案是相互独立的,不会相互影响,即使左、右括号添加在同一个间隙,因为不能存在"()“的形式,此处只能为类似”))(("的一种形式,故总的方案数等于左括号的方案数 × 右括号的方案数。
(2)单独考虑添加左括号,若以右括号为分割点, 将整个序列进行分割,因为分割后的子串中均为左括号, 添加任意数目的左括号方案数均为一种,那么此时,我们仅需考虑添加不同数量的左括号的方案数即可。
(3)右括号同理
动态规划:
f[i][j]的状态表示为:只考虑前 i 部分,左括号比右括号多 j 个的所有方案的集合
状态计算:
(1) 若str[i] == ‘(’,易推算出转移方程为f[i][j] = f[i - 1][j - 1]
(2) 若str[i] == ‘)’,则在只考虑前 i - 1部分时,此时左括号数量最多比右括号多 j + 1个,才可能在第 i 部分通过添加或者不加左括号,达到左括号的数量比右括号多 j 个,故状态转移方程为f[i][j] = f[i - 1][j + 1] + f[i - 1][j] + … + f[i - 1][0],通过完全背包的思维优化这一段转移方程,使得该部分总复杂度由 O(n^3) 降为O(n^2),优化的状态转移方程为f[i][j] = f[i - 1][j + 1] + f[i][j - 1] (为了防止越界,f[i][0]需要特判)。
#include 总结
总的来说这场题目质量我觉得还是蛮高的,考点考的也很全面,思维方面居多,算法主考DP,只考了一道复杂的数据结构但是也可以优化,填空压轴图论考了最短路径的模板题应该添加的其余信息只是增加了码量。我当时的做题情况应该是拿了50分左右就得到了省一的成绩,正常把签到写出来(填空1.2、大题1,其余模拟骗分)就可以省三了。













