苏剑林GlobalPointer系列阅读笔记

实体识别GlobalPointer

原文链接： https://spaces.ac.cn/archives/8373

GlobalPointer：利用全局归一化的思路来进行命名实体识别（NER），可以无差别地识别嵌套实体和非嵌套实体，在非嵌套（Flat NER）的情形下它能取得媲美CRF的效果，而在嵌套（Nested NER）情形它也有不错的效果。

基本思路

假设要识别文本序列长度为n，简单起见先假定只有一种实体要识别，并且假定每个待识别实体是该序列的一个连续片段，长度不限，并且可以相互嵌套（两个实体之间有交集）该序列有n(n+1)/2个个“候选实体”。我们要做的就是从这n(n+1)/2个“候选实体”里边挑出真正的实体，其实就是一个“n(n+1)/2选k”的多标签分类问题。如果有m种实体类型需要识别，那么就做成m个“n(n+1)/2选k”的多标签分类问题。

数学形式

GPLinker：基于GlobalPointer的实体关系联合抽取

原文链接 https://spaces.ac.cn/archives/8888

基本思路

关系抽取乍看之下是三元组(s,p,o)（即subject, predicate, object)的抽取，但落到具体实现上，它实际是“五元组”(sh,st,p,oh,ot)的抽取，其中sh,st分别是s的首、尾位置，而oh,ot则分别是o的首、尾位置。
从概率图的角度来看，我们可以这样构建模型：

1、设计一个五元组的打分函数S(sh,st,p,oh,ot)；

2、训练时让标注的五元组S(sh,st,p,oh,ot)>0，其余五元组则S(sh,st,p,oh,ot)<0；

3、预测时枚举所有可能的五元组，输出S(sh,st,p,oh,ot)>0的部分。

然而，直接枚举所有的五元组数目太多，假设句子长度为l，p的总数为n，即便加上sh≤st和oh≤ot的约束，所有五元组的数目也有：

简化分解

S(sh,st)、S(oh,ot)分别是subject、object的首尾打分，通过 S(sh,st)>0 和 S(oh,ot)>0 来析出所有的subject和object。至于后两项，则是predicate的匹配，S(sh,oh|p)这一项代表以subject和object的首特征作为它们自身的表征来进行一次匹配，如果我们能确保subject内和object内是没有嵌套实体的，那么理论上S(sh,oh|p)>0就足够析出所有的predicate了，但考虑到存在嵌套实体的可能，所以我们还要对实体的尾再进行一次匹配，即S(st,ot|p)这一项。

此时，训练和预测过程变为：

1、训练时让标注的五元组S(sh,st)>0、S(oh,ot)>0、S(sh,oh|p)>0、S(st,ot|p)>0，其余五元组则S(sh,st)<0、S(oh,ot)<0、S(sh,oh|p)<0、S(st,ot|p)<0；

2、预测时枚举所有可能的五元组，逐次输出S(sh,st)>0、S(oh,ot)>0、S(sh,oh|p)>0、S(st,ot|p)>0的部分，然后取它们的交集作为最终的输出（即同时满足4个条件）。

GPLinker：基于GlobalPointer的事件联合抽取

原文链接 https://spaces.ac.cn/archives/8926

在之前的关系抽取模型GPLinker的基础上，结合完全子图搜索，设计一个比较简单但相对完备的事件联合抽取模型。

完全子图

事件划分，一个很自然的想法就是直接把所有具有同一事件类型的论元聚合起来作为一个事件，但这也是不够完备的，因为同一个输入可能有多个同一类型的事件。如果加上触发词呢？还是不够，多个同一类型的事件还可能公用同一个触发词，比如DuEE有一个样本是“主要成员程杰、王绍伟被法院一审判处有期徒刑22年和20年。”，分别有两个事件“程杰判处有期徒刑22年”和“王绍伟判处有期徒刑20年”，触发词都是“有期徒刑”，事件类型都是“入狱”。

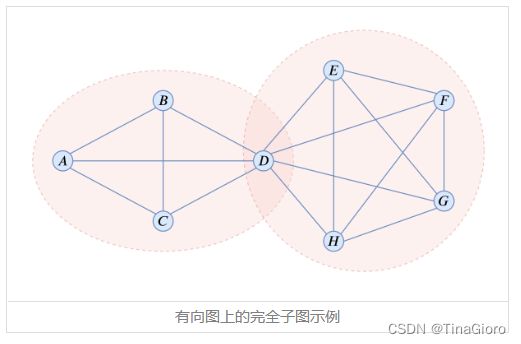
所以，我们需要设计一个额外的模块来做事件划分。我们认为，同一事件的各个论元是有联系的，这种联系可以用无向图来描述。也就是说，我们将每个论元看成是图上的一个节点，而同一事件任意两个论元的节点可以连上一条边而成为相邻节点，而如果两个论元从未出现在同一事件中，那么对应的节点则没有边（不相邻）。这样一来，同一事件的任意两个节点都是相邻的，这我们称为“完全图（Complete Graph）”，也称为“团（Clique）”，事件划分转化为图上的完全子图搜索。

那么如何构建这个无向图呢？我们沿用TPLinker的做法，如果两个论元实体有关系，那么它们的(首, 首)和(尾, 尾)都能匹配上，我们可以像关系抽取的GPLinker一样，用GlobalPointer来预测它们的匹配关系。特别地，由于我们只需要构建一个无向图，所以我们可以mask掉下三角部分，所有的边都只用上三角部分描述。

搜索算法

递归搜索算法：

1、枚举图上的所有节点对，如果所有节点对都相邻，那么该图本身就是完全图，直接返回；如果有不相邻的节点对，那么执行步骤2；

2、对于每一对不相邻的节点，分别找出与之相邻的所有节点集（包含自身）构成子图，然后对每个子图集分别执行步骤1。

以上图为例，我们可以找出B、E是一对不相邻节点，那么我们可以分别找出其相邻集为{A,B,C,D}和{D,E,F,G,H}，然后继续找{A,B,C,D}和{D,E,F,G,H}的不相邻节点对，发现找不到，所以{A,B,C,D}和{D,E,F,G,H}都是完全子图。注意这个不依赖于不相邻节点对的顺序，因为对于“所有”不相邻节点对我们都要进行同样的操作，比如我们又找到A、F是一对不相邻节点，那我们同样要找其相邻集{A,B,C,D}和{D,E,F,G,H}并递归执行。所以，在整个过程中，我们可能会得到很多重复结果，但不会漏了某个结果，也不会搜识别顺序影响，最后再去重即可。

此外，每次搜索的时候，我们只需要对同一事件类型的节点进行搜索，而多数情况下同一事件类型的论元只有个位数，所以上述算法看似复杂，实际运行速度还是很快的。