MPC(模型预测控制)_附matlab例程

写在前面：
  本文为科研理论笔记的第二篇，其余笔记目录传送门：

理论笔记专栏目录

  介绍结束下面开始进入正题：

1 基本概念

1.1 最优控制

​   最优控制(optimal control)：在约束条件下的最优表现，约束条件即物理限制，而对于最优的评判往往需要具体问题具体分析。

​   一个SISO系统的框图如下所示：

​ 对于误差$e$，从轨迹跟踪的角度出发，${\int }_0^t{e}^{2}dt$ 越小表示系统追踪效果越好；而从输入的角度出发，${\int }_0^t{u}^{2}dt$ 越小表示系统的输入(能耗)越小。在上述条件下，即可构造系统的代价函数(cost function)：$J={\int }_0^{t}q{e}^2+r{u}^{2}dt$。其中的$q$和$r$称为调节参数，最优化过程即使设计一个控制器使得$J=J_{min}$。若使得$q>>r$ 则表示在最优化的过程中更看重误差，反之若$r>>q$ 则表示在最优化的过程中更看重输入。

​   拓展到MIMO系统，系统的状态空间方程一般可以描述为：
$$\{\begin{array}{l}\dot{x}=Ax+Bu\\ y=Cx\end{array}$$
​其中$x=[x_1,\cdots ,x_n{]}^T$为系统状态,$u=[u_1,\cdots ,u_n{]}^T$为系统输入。

​   类似SISO系统，可设$J={\int }_0^x{e}^{T}Qe+u^{T}Rudt$ 。其中对角阵$Q=\left[\begin{array}{ccc}{q}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & q_n\end{array}\right]$和$R=\left[\begin{array}{ccc}{r}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & r_n\end{array}\right]$称为调节矩阵，$q_1\cdots q_n、r_1\cdots r_n$ 称为最优化过程中的权重系数，可相应的调整$x_1\cdots x_n、u_1\cdots u_n$ 的优化权重。

1.2 MPC

​   MPC(model predictive control)：模型预测控制，指通过模型预测系统在某一未来时间段内的表现来进行优化控制，因为其多用于数位控制，所以在分析时主要采用离散型状态空间表达式来进行分析，例如对于四轮阿克曼底盘的小车，其离散状态空间表达式可参考前一篇笔记：

四轮移动机器人(小车)数学建模

​   基于模型的预测：在MPC算法中，需要一个描述对象动态行为的模型，这个模型的作用是预测系统未来的动态，即能够根据系统$k$时刻的状态$x_k$和$k$时刻的控制输入$u_k$，预测到$k+1$时刻的输出$y_{k+1}$。在这里$k$时刻的输入正是用来控制系统$k+1$时刻的输出，使其最大限度的接近$k+1$时刻的输出期望值。故我们强调的是该模型的预测作用，而不是模型的形式。

​   预测区间：规定了希望未来能被预测到多久。从当前时刻$k$到$k+N$的时间区间。

​   控制区间：控制区间的选择就是一个最优化的问题，其代价函数$J={\sum }_{i=0}^{N-1}{e}_{k+i}^{T}Q{e}_{k+i}+u_{k+i}^{T}R{u}_{k+i}+e_{k+N}^{T}F{e}_{k+N}$ ，其中$e_{k+N}^{T}F{e}_{k+N}$ 表示最终代价，即最后$k+N$时刻的误差代价。

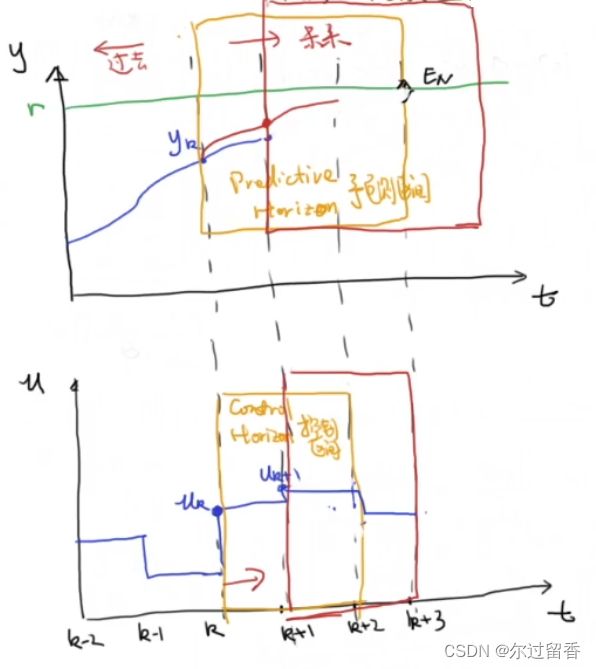
​   MPC主要分为三步：

​   step1:在$k$时刻(当前时刻)，测量或估计系统的当前状态$x_k$ (若$x_k$不可直接测得，则一般采用状态观测器进行估计)；

​   step2:基于预测控制量$u_k、u_{k+1}...u_{k+N-1}$ 来进行最优化控制；

​   step3:只将$u_k$ 施加给系统，进行滚动优化控制。
​

2 最优化建模

​   MPC的重点在于step2中如何进行最优化控制，最优化的方法很多，下面主要推导一种常用的二次规划(Quadratic Programming)的方法。

​   二次规划的一般形式为：$min(Z^{T}QZ+C^{T}Z)$，其中$Z^{T}QZ$为二次型项，$C^{T}Z$为线性项。对于二次规划问题的处理当前Matlab、Python、C++等都有很成熟的方法了，所以关键就在于如何将自己的模型化为二次规划的一般形式。

​   设系统的线性离散状态空间表达式为$x_{(k+1)}=A{x}_{(k)}+B{u}_{(k)}$ ，其中$x=[x_1,\cdots ,x_n{]}^T,u=[u_1,\cdots ,u_p{]}^T$，状态矩阵$A$为$n\times n$矩阵，输入矩阵$B$为$n\times p$矩阵。

​   在$k$时刻，定义：
$$X_k={\left[\begin{array}{c}{x}_{(k|k)}\\ x_{(k+1|k)}\\ ⋮\\ x_{(k+N|k)}\end{array}\right]}_{(N+1)n\times 1}；U_k={\left[\begin{array}{c}{u}_{(k|k)}\\ u_{(k+1|k)}\\ ⋮\\ u_{(k+N-1|k)}\end{array}\right]}_{Np\times 1}$$
其中$N$为预测区间，以$x(k+1|k)$为例，括号内|左边的$k+1$表示预测的$k+1$时刻的状态量，括号内|右边的$k$表示在$k$时刻做出的预测。

​   为了简化分析，设输入$y=x$，参考量$r=0$，则误差$e=y-r=x$，代价函数可化为：
$$\begin{gathered} J=\sum _{i=0}^{N-1}{x}_{(k+i|k)}^{T}Q{x}_{(k+i|k)}+u_{(k+i|k)}^{T}R{u}_{(k+i|k)}+x_{(k+N|k)}^{T}F{x}_{(k+N|k)} \\ 即：J=误差加权和+输入加权和+终端误差 \end{gathered}$$
​ 由系统初始条件$x_{(k|k)}=x_{(k)}$，可递推得：
$$\begin{gathered} x_{(k+1|k)}=A{x}_{(k|k)}+B{u}_{(k|k)}=A{x}_{(k)}+B{u}_{(k|k)}; \\ {x}_{(k+2|k)}=A{x}_{(k+1|k)}+B{u}_{(k+1|k)}=A^2{x}_{(k)}+AB{u}_{(k|k)}+B{u}_{(k+1|k)}; \\ ⋮ \\ {x}_{(k+N|k)}=A^n{x}_{(k)}+A^{N-1}B{u}_{(k|k)}+\cdots +B{u}_{(k+N-1|k)}; \end{gathered}$$
​ 整理上面$N+1$个式子可得(其中的$0$表示$n\times p$ 的零矩阵)：
$$X_k=\left[\begin{array}{c}I\\ A\\ A^2\\ ⋮\\ A^N\end{array}\right]x_{(k)}+\left[\begin{array}{cccc}0& 0& \cdots & 0\\ B& 0& \cdots & 0\\ AB& B& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ A^{N-1}B& A^{N-2}B& \cdots & B\end{array}\right]U_k$$
​ 定义：
$$M={\left[\begin{array}{c}I\\ A\\ A^2\\ ⋮\\ A^N\end{array}\right]}_{(N+1)n\times n}；C={\left[\begin{array}{cccc}0& 0& \cdots & 0\\ B& 0& \cdots & 0\\ AB& B& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ A^{N-1}B& A^{N-2}B& \cdots & B\end{array}\right]}_{(N+1)n\times Np}$$
​ 即有：$X_k=M{x}_{(k)}+C{U}_k$，其意义是由$k$时刻的状态量和预测输入量可得出预测状态量。

​   再来将代价函数$J$化为紧凑形式，例如其中误差加权和及终断误差可化为：
$$\begin{gathered} \sum _{i=0}^{N-1}{x}_{(k+i|k)}^{T}Q{x}_{(k+i|k)}+x_{(k+N|k)}^{T}F{x}_{(k+N|k)} \\ =x_{(k|k)}^{T}Q{x}_{(k|k)}+x_{(k+1|k)}^{T}Q{x}_{(k+1|k)}+\cdots +x_{(k+N-1|k)}^{T}Q{x}_{(k+N-1|k)}+x_{(k+N|k)}^{T}F{x}_{(k+N|k)} \\ =X_k^T\left[\begin{array}{ccc}Q& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & F\end{array}\right]X_k \end{gathered}$$
​ 定义：
$$\overline{Q}=\left[\begin{array}{ccc}Q& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & F\end{array}\right]；\overline{R}=\left[\begin{array}{ccc}R& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & R\end{array}\right]$$
​ 则有：
$$\begin{gathered} J=\sum _{i=0}^{N-1}{x}_{(k+i|k)}^{T}Q{x}_{(k+i|k)}+u_{(k+i|k)}^{T}R{u}_{(k+i|k)}+x_{(k+N|k)}^{T}F{x}_{(k+N|k)} \\ =X_k^T\overline{Q}{X}_K+U_k^T\overline{R}{U}_k \end{gathered}$$
​ 将$X_k=M{x}_{(k)}+C{U}_k$代入$J=X_k^T\overline{Q}{X}_k+U_k^T\overline{R}{U}_k$：
$$\begin{gathered} J=X_k^T\overline{Q}{X}_K+U_k^T\overline{R}{U}_k \\ =(M{x}_{(k)}+C{U}_k{)}^T\overline{Q}(M{x}_{(k)}+C{U}_k)+U_k^T\overline{R}{U}_k \\ =(x_{(k)}^T{M}^T+U_k^T{C}^T)\overline{Q}(M{x}_{(k)}+C{U}_k)+U_k^T\overline{R}{U}_k \\ =x_{(k)}^T{M}^T\overline{Q}M{x}_{(k)}+x_{(k)}^T{M}^T\overline{Q}C{U}_k+U_k^T{C}^T\overline{Q}M{x}_{(k)}+U_k^T{C}^T\overline{Q}C{U}_k+U_k^T\overline{R}{U}_k \\ =x_{(k)}^T{M}^T\overline{Q}M{x}_{(k)}+2x_{(k)}^T{M}^T\overline{Q}C{U}_k+U_k^T(C^T\overline{Q}C+\overline{R})U_k \end{gathered}$$
​ 定义：$G=M^T\overline{Q}M、E=M^T\overline{Q}C、H=C^T\overline{Q}C+\overline{R}$；即有：
$$J=x_{(k)}^{T}G{x}_{(k)}+U_k^{T}H{U}_k+2x_{(k)}^{T}E{U}_k$$
​ 注意到上式第一项$x_{(k)}^{T}G{x}_{(k)}$仅与初始状态$x_{(k)}$有关，不影响后续优化，后两项形同$Z^{T}QZ+C^{T}Z$，即可用于二次规划得到理想的输入。
  至此MPC算法就介绍完成啦，上面的公式希望大家初学的时候都能手推一遍以便于更好的理解，最后附上一个简单的matlab例程供大家参考。

MPC例程github传送门，注意科学上网