机器学习与数据挖掘知识归纳（二）

四. 决策树

1. 决策树学习的基本思想

决策树学习每次划分时，要选择使得信息增益最大的划分方式（局部最优），以此来递归构建决策树。通常包括 3 个步骤：特征选择、决策树生成和剪枝。
具体来说：决策树从根节点开始，测试待分类项中所有特征属性，选择最好的属性进行划分，并按照其每个属性值来创建子节点，直到到达叶子节点，最后进行剪枝，将叶子节点存放的类别作为决策结果，以此来实现学习。

2. 分类错误率，熵，信息增益的概念，如何根据不同度量选择最佳划分

决策树学习的关键在如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别， 即结点的 “纯度”（purity）越来越高
（1）分类错误率：
直观地将分类误差作为损失。

（2）熵：

（3）信息增益：

（4）GINI指数：

3. 缺失值对决策树有何影响？

• 影响不纯度的计算
• 影响如何向子节点分配带有缺失值的实例
• 影响带有缺失值的测试实例如何分类

4. 给定混淆矩阵，分类效果度量不同指标的含义及计算方法。

5. 评估分类器性能的留一法和 k 折交叉验证

（1）留一法：
每次只留下一个样本做测试集，其它样本做训练集，如果有k个样本，则需要训练k次，每次有k-1个样本，测试k次，每次有1个样本。留一法计算最繁琐，但样本利用率最高。适合于小样本的情况。可以说是交叉验证的特例。
（2）K折交叉验证：
将全部训练集 S分成 k个不相交的子集，假设 S中的训练样例个数为 m，那么每一个子 集有 m/k 个训练样例，相应的子集称作 {s1,s2,…,sk}。
每次从分好的子集中里面，拿出一个作为测试集，其它k-1个作为训练集
根据训练训练出模型或者假设函数。
把这个模型放到测试集上，得到分类率。
计算k次求得的分类率的平均值，作为该模型或者假设函数的真实分类率。

6. 过拟合和欠拟合

五. 神经网络

1. 神经网络如何学习？ 有何特点？

（1）神经网络含义：
通过调整权值对训练数据进行正确的分类，来进行学习，从而在测试阶段之后，对未知数据进行分类；具体来说，感知器对输入一组x加权一组w求和，再减去偏置因子,若结果大于0，输出值g=1，反之g=0。神经网络需要很长时间的训练；神经网络对有噪声和不完整的数据具有较高的容忍度。
（2）神经网络特点：

• 许多简单的类似神经元的阈值开关单元。
• 神经元之间的加权互连。
• 高度并行的分布式处理。
• 通过调整连接权重进行学习

（3）神经网络适合的问题域：

• 输入是高维离散值或实值
• 输出是离散值或实值、矢量值
• 目标函数的功能未知
• 不需要去解释结果（黑盒模型）

2. 梯度下降算法

本节参考文章：神经网络之梯度下降法及其实现
（1）梯度下降思路：
从一个任意的初始权值向量开始；反复修改它； 每一步都沿着误差面以产生最陡峭下降的方向改变权值向量。

此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点！
α 在梯度下降算法中被称作为学习率(learning_rate)或者步长，梯度前加一个负号，就意味着朝着梯度相反的方向前进，梯度的方向实际就是函数在此点上升最快的方向。
举例：
目标函数为
初始点为
梯度为
梯度下降法过程如下：

一般我们取E（w）均方误差代价函数，作为上面的J（w）

3. 多层神经网络使用什么算法进行训练？

本节参考文章：一文弄懂神经网络中的反向传播法——BackPropagation
反向传播算法：
传播的是损失，也就是根据最后的损失，计算网络中每一个节点的梯度，这里利用了链式法则，使得梯度的计算并不是很复杂。
举例：
给出输入数据i1,i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。

六. 贝叶斯学习

1. 根据贝叶斯理论，如何计算一个假设h 成立的后验概率？

其中 H 是假设，D 是数据，P(H)是先验概率（先验概率顾名思义是看到数据前的猜测）， P(H|D)是后验概率（后验概率顾名思义是拿到数据之后的猜测）， P(D) 是数据发生的概率，P(D|H)是在这个假设下数据发生的概率，也叫似然函数 。

2. 极大后验概率假设和极大似然假设有何区别？

极大后验假设：学习器考虑候选假设集合H并在其中寻找给定数据D时，可能性最大的假设h（或者存在多个这样的假设时选择其中之一）。这样的具有最大可能性的假设h被称为极大后验假设。（P(D)不依赖于H，因此可以省略）
极大似然估计的核心思想是：认为当前发生的事件是概率最大的事件。因此就可以给定的数据集，使得该数据集发生的概率最大来求得模型中的参数。极大似然估计只关注当前的样本，也就是只关注当前发生的事情，不考虑事情的先验情况。

3. 最小描述长度的基本思想

推导过程：


上述圆圈两个部分就等价于上述MDL公式。
解读：
Lc2(D|h)：在给定假设 h 时，训练数据 D 的描述长度。也即是发送者和接收者都知道假设 h 时描述数据 D 的最优编码。
Lc1(h)：在假设空间 H 的最优编码下 h 的描述长度。
最小描述长度准则默认选用使这两个描述长度的和最小化的假设 h。
MDL准则，实际上是假设复杂性（模型复杂度）和假设产生错误的数量之间对的一个折中。MDL 倾向于选择一个产生少量错误而且较短的假设，而不是能完美分类训练数据的较长的假设。
扩展解读：
从信息论的角度看最小描述长度公式，可以把学习过程(以分类为例)理解为以下过程：
发送者需要将训练数据 D (包含特征和分类结果)、拟合这些数据的假设 h 以编码的方式传送给接收者。在此处明确一下发送者究竟需要传送哪些必须的信息呢？

• 训练数据——为了尽量降低编码长度，我们假设发送者和接收者都知道每一个训练数据的特征信息，所以特征信息就不用编码传送。而每一个训练数据的分类结果必须传送吗？答案是N0，因为我们还要将假设 h 编码传送。如果训练数据的分类结果label 和通过假设 h 预测出的结果一致，那么我们就不需要传送这个数据的标签信息。只有当训练数据预测出错时，才需要将正确的标签信息传送。
• 假设——假设 h 必须编码传送。并且 h 越复杂， 编码长度越大。如若不明白，可以假设学习器是决策树，对树的编码方法随着决策树节点和边的增长而增加。
  其中对训练数据的编码和对假设的编码分别记为 C1 和 C2。

至此可以看出，当 C1 和 C2 分别选取MDL准则中对应的最佳编码方式时训练数据和假设的编码长度之和最小。所选的假设 h 也就是 极大后验假设。

4. 贝叶斯最优分类器的基本思想

新实例的最可能分类是通过结合所有假设的预测而得到，并按其后验概率加权，同时考虑所有的假设并且进行加权。其中 V 是预测分类所有值的集合，vj是这种分类的一种可能


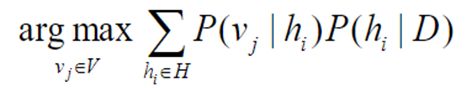
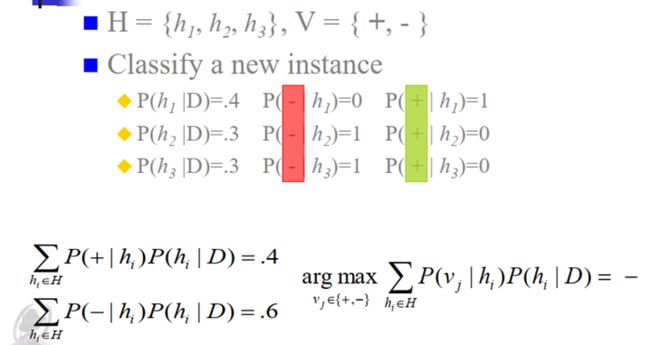
这种方法使新实例被正确分类的概率最大化；
在相同的假设空间和相同的先验知识下，没有其他分类方法能超过本方法的平均水平。
该方法做出的预测可以对应于H中不包含的假设。

5. 朴素贝叶斯分类算法

vNB—朴素贝叶斯分类器输出的目标值
训练集D的每个实例x由n个属性值的组合来描述；
每个目标值vj在训练数据中出现的频率
P(ai|vj)：不同的属性值的数量× 不同目标值的数量。
应用举例：

6. 贝叶斯信念网络的预测和诊断

节点都与一个概率函数相关联，该函数将节点的父变量的一组特定值作为输入，并给出该节点的概率。连接的边代表条件性的依赖关系；不连接的节点代表相互独立的变量。
贝叶斯最优分类器的成本往往太高，无法应用。朴素贝叶斯分类器的条件独立假设太严格，特别是对那些属性之间有一定相关性的分类问题。贝叶斯网络允许使用变量子集（部分属性）的条件独立性假设。

7. 偏差方差分析

对于某个特定的模型来说，它的泛化误差（Generation Error）可以分为三部分：模型预测值的方差（variance）、预测值相对真实值的偏差（bias）、样本本身存在的噪声（noise），可以用下面的公式进行表示：
D为训练集、X为测试样本


规律：复杂模型偏差小，方差大； 简单模型偏差大，方差小。