机器学习--感知机学习算法

以下只给出了感知机算法的Python代码实现，想从头开始了解机器学习以及感知机模型的推荐李航老师的统计学习方法蓝宝书

感知机算法原始形式

# 感知机(原始形式)
import numpy as np
# 创建测试集，包含三个实例点和两个类别
def createDataSet():
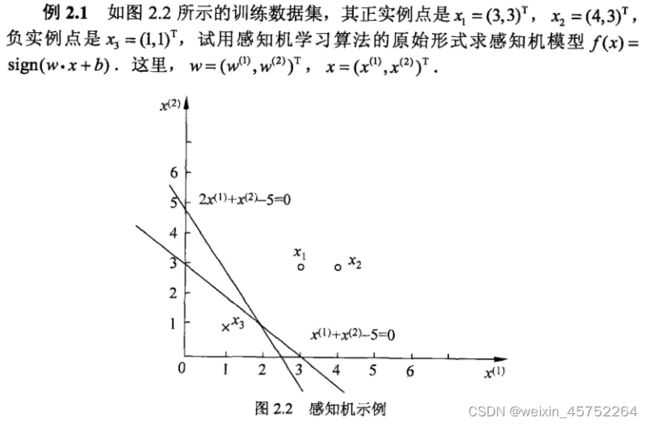
    group = np.array([[3,3],[4,3],[1,1]])
    labels = [1, 1, -1]
    return group,labels

# 定义感知机分类器
def perceptronClassify(trainGroup,trainLabels):
    global w,b
    isFind=False
    numSamples=trainGroup.shape[0]
    mLenth=trainGroup.shape[1]
    w=[0]*mLenth
    b=0
    while(not isFind):
        for i in range(numSamples):
            if cal(trainGroup[i],trainLabels[i])<=0:
                print('w:%s，b:%s'%(w,b))
                update(trainGroup[i],trainLabels[i])
            elif i==numSamples-1:
                print('w:%s，b:%s'%(w,b))
                isFind=True


def cal(row,trainsLabels):
    global w,b
    res=0
    for i in range(len(row)):
        res+=row[i]*w[i]
    res += b
    res*=trainsLabels
    return res

def update(row,trainsLabels):
    global w,b
    for i in range(len(row)):
        w[i]+=trainsLabels*row[i]
    b+=trainsLabels
group,labels=createDataSet()
perceptronClassify(group,labels)

运行结果

D:\Python\Python37\python.exe D:/ML/perceptron.py
w:[0, 0]，b:0
w:[3, 3]，b:1
w:[2, 2]，b:0
w:[1, 1]，b:-1
w:[0, 0]，b:-2
w:[3, 3]，b:-1
w:[2, 2]，b:-2
w:[1, 1]，b:-3

Process finished with exit code 0

感知机算法对偶形式

# 感知机 对偶形式
import numpy as np
# 创建测试集，包含三个实例点和两个类别
def createDataSet():
    group = np.array([[3,3],[4,3],[1,1]])
    labels = [1, 1, -1]
    return group,labels

# 构造Gram矩阵
def Gram(trainGroup):
    mLenth=trainGroup.shape[0]
    gram=np.zeros((mLenth,mLenth))
    for i in range(mLenth):
        for j in range(mLenth):
            gram[i][j]=np.dot(trainGroup[i],trainGroup[j])
    return gram

def dualperceptronClassify(trainGroup,trainLabels):
    global a,b
    isFind = False
    numSamples = trainGroup.shape[0]
    # mLenth = trainGroup.shape[1]
    a=[0]*numSamples
    b=0
    gram=Gram(trainGroup)
    while not isFind:
        for i in range(numSamples):
            if cal(gram,trainLabels,i)<=0:
                w,h=cal_wb(trainGroup,trainLabels)
                print('a:%s,w:%s,b:%s'%(a,w,b))
                update(i,trainLabels)
            elif i==numSamples-1:
                isFind=True

# 误分条件
def cal(gram,trainLabels,key):
    global a,b
    res=0
    for i in range(len(trainLabels)):
        res += a[i] * trainLabels[i] * gram[key][i]
    res += b
    res *= trainLabels[key]
    return res
# 更新参数a,b
def update(key,trainlabels):
    global a,b
    a[key]+=1
    b+=trainlabels[key]
# 根据a求参数w
def cal_wb(group,labels):
   global a,b
   w=[0]*group.shape[1]
   for i in range(len(labels)):
       w+=a[i]*labels[i]*group[i]
   return w

group,labels=createDataSet()
dualperceptronClassify(group,labels)

运行结果

D:\Python\Python37\python.exe D:/ML/perceptron1.py
a:[0, 0, 0],w:0,b:0
a:[1, 0, 0],w:3,b:1
a:[1, 0, 1],w:2,b:0
a:[1, 0, 2],w:1,b:-1
a:[1, 0, 3],w:0,b:-2
a:[2, 0, 3],w:3,b:-1
a:[2, 0, 4],w:2,b:-2

Process finished with exit code 0

最后，还是不太理解对偶形式相比于原始形式的优点在哪