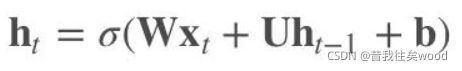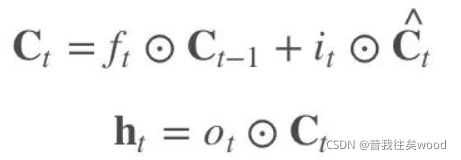【神经网络】学习笔记十七——IRNN:初始化矩阵RNN
首先对IRNN进行了总的简要介绍,后面进行了原理剖析和为什么引进了IRNN,以及最后总结了它的优点和特点。
目录
一、说在前面
1. 传统RNN的问题
2. IRNN做出的改变
3. 提出的IRNN的重点
二、引入:传统RNN存在的问题
1. 传统RNN存在的问题
2. 改进的LSTM和GRU的问题
3. IRNN的引入
总结
一、说在前面
IRNN(Identity Matrix RNN),初始化RNN,即初始化矩阵循环神经网络。
1. 传统RNN的问题
传统RNN由于在时间上存在参数共享(U用来更新cell状态),造成梯度消失/爆炸问题;改进的LSTM和GRU在解决层内梯度消失/爆炸问题的同时,梯度在层间仍会存在衰减(即多层RNN时),所以LSTM和GRU难以做成多层网络。并且,LSTM和GRU也存在难以捕捉更长的时序信息的问题。此外,传统RNN由于层内神经元相互联系,难以对神经元的行为做出合理的解释。
2. IRNN做出的改变
从字面意思上看也能看出来,是将一个矩阵进行初始化的RNN。其实初始化的是循环系数矩阵,将循环系数矩阵U初始化为单位矩阵,搭配上ReLU作为激活函数,并稍微改变了一下计算过程(将隐藏层状态更新的矩阵U变为了向量u),完美解决了梯度爆炸问题,也顺便解决了LSTM和GRU由于不可并行带来的计算复杂性,可以搭建多层。
3. 提出的IRNN的重点
(1)改变计算过程:将U改成了u,使RNN层内神经元解耦,使它们相互独立,提高神经元的可解释性;
(2)有序序列采用ReLU作为激活函数,完美解决梯度消失/爆炸问题,同时模型更具鲁棒性;
(3)可以处理比LSTM更长的时序信息;
(4)改变计算过程同时也简化了计算,可以搭建更多层;
二、引入:传统RNN存在的问题
1. 传统RNN存在的问题
RNN隐层的计算公式如下:
设T时刻的目标函数为J,则反向传播到t时刻的梯度计算:
U为循环系数矩阵,diag(σ′(hk+1)为激活函数的雅可比矩阵。可以看到,RNN的梯度计算依赖于激活函数的对角矩阵矩阵diag(σ′(hk+1)跟系数矩阵U的连积,即该矩阵的n次幂。
则当:
(1)对角元素有一个大于1时,n次连积后会趋近无穷大;
(2)对角元素有一个小于1时,n次连积后会趋近无穷小;
这样会出现梯度消失和梯度爆炸问题。因为RNN的激活函数一般使用sigmoid或tanh函数。前者的导数sigmoid(1-sigmoid),最大值0.25,图像两端趋于0;后者的导数1-tanh2,最大值为1,图像两端趋于0。
这样一来,两个激活函数的大多数导数取值都小于1,因此它们与循环权重稀疏矩阵相乘构成的对角矩阵元素绝大部分小于1(可能等于1,但不可能大于1),连积后梯度指数级下降,造成了梯度消失问题。
而在RNN中使用ReLU激活函数,由于ReLU在x>0时导数恒为1,因此若U中元素有大于1的,则构成的对角矩阵也会有大于1的,连积造成梯度爆炸。
为此提出了解决方案:门控函数LSTM和GRU。
2. 改进的LSTM和GRU的问题
LSTM在RNN的基础上增加了遗忘门,将原来的一个记忆h(t)转换为两个记忆:长时记忆C(t)和短时(工作)记忆h(t)。其中长时记忆C(t)由以前所有时间cell的记忆的一部分和此刻时间cell的状态的一部分拼合而成,共同构成了新的长时记忆C(t),并传入下一时刻的cell。公式如下,其中ft和it分别是两个概率值:
引入门控的目的是将激活函数导数的连乘变成加法。其反向传播时有两个隐态:
其中仅长时记忆C(t)参与反向传播:
可以看到,激活函数导数矩阵变成了加法的第二部分。这里起作用的是加号前的项,f(t+1)控制着梯度衰减的程度。当f=1时,即使后面的项很小,梯度仍然能很好地传到上一时刻;f=0时,即上一时刻信号对此刻不造成任何影响,因此可以为0。(f为长时记忆C项的概率)
门控函数虽然有效缓解了梯度消失问题,但处理更长序列的时候仍然不可避免。但尽管如此,LSTM和GRU在处理NLP任务已经表现很好了,其实门控函数最主要的问题是门的存在使得计算过程无法并行,且大大增加了计算复杂性。
并且,在多层LSTM中,由于还是采用tanh函数,所以层与层之间的梯度消失仍没有解决(这里主要是受加号后面项的影响)。所以,现在大多数LSTM最多采用2-3层,不会超过四层。
3. IRNN的引入
Hitton于2015年提出使用ReLU作为RNN的激活函数,但其导致的梯度爆炸问题在上面已经说明。由此,IRNN将权重矩阵初始化为单位矩阵,并将偏置置为0,IRNN的I因此得名:Identity Matrix!
(1)梯度截断
在反向传播中,梯度消失和爆炸是一个渐变的过程,梯度截断的意思就是说,在渐变的过程中,传递几步就人为的去截断,矩阵连乘几次就截断,然后强行拉回正常值水平,再进行梯度下降,就不会产生梯度消失。该方法对解决梯度问题比较有效,但人为的因素,并且拉回的值也不一定准确,那么有没有更好的方法呢?
(2)IRNN的引入
为了解决梯度问题,IRNN引入了ReLU作为激活函数,并且将层内神经元独立开来。计算公式如下:
权重系数从矩阵U变成了向量u。即在t时刻,每个神经元只接受此刻的输入以及t-1时刻自身的状态作为输入。
这就是独立开来的原因:RNN的权重系数是U,意味着t时刻,接受t-1时刻所有cell的状态作为输入。IRNN的这种操作导致了层内神经元的独立性,每个神经元只被自己的状态所影响。
现在来看一下梯间问题:
与传统RNN作为对比,此时的连积不再是矩阵操作,而是将激活函数的导数与循环权重系数独立起来,使用ReLU也变得顺理成章。至此,梯度问题完美解决。
(3)IRNN其他的优点
神经元之间的相互连接依靠层间交互完成。也就是说,下一层的神经元会接受上一层神经元所有的输出作为输入(相当于全连接层)。
有人证明了两层的IRNN相当于一层激活函数为线性函数,循环权重为可对角化矩阵的传统RNN。
IRNN可实现多层堆叠。因为多层堆叠结构,层间交互是全连接,所以可以进行改进,比如全连接改为CNN连接,也可以引入BN,残差连接等。
总结
本文介绍了
(1)RNN由于sigmoid和tanh作为激活函数,导致的激活函数对角矩阵跟系数矩阵U连积梯度消失问题,ReLU作为激活函数又会导致梯度爆炸问题。
(2)引入门控函数LSTM和GRU一定程度上解决了此问题,但其带来的计算复杂性又很大,而且层间梯度问题也没有解决。
(3)最终通过初始化权重系数矩阵U为单位矩阵,改变权重系数矩阵U为向量u:解决了层内神经元之间的耦合性,提高神经元的独立性,并改变了反向传播的算法,将激活函数的导数与循环系数向量独立起来,解决了梯度问题,由此可以用ReLU作为激活函数而不会带来梯度爆炸,并简化了计算过程。
(4)同时,还可以通过改变层间神经元的全连接方式,实现多层IRNN堆叠,而不用带来层间梯度问题。