【超分辨率】Closed-loop Matters: Dual Regression Networks for Single Image Super-Resolution

前言

这是一篇CVPR2020年的文章，创新点主要在于不仅让网络学习LR->HR的映射，还学习HR->LR来减小映射空间，解决不适定的问题。

0 摘要

用基于学习的方法来解决SR问题现在已经有很多比较成熟的算法，但是依然存在两个比较难解决的问题：

1.学习从LR到HR的映射是一个典型的不适定问题，因为从一个HR图像下采样恢复到LR图像这个过程中，许多个不同的HR图像可能会恢复到同一个LR图像，也就是多个输入可能对应同一个解，这也就导致了映射函数的空间非常大，很难去学习到一个非常完备的映射函数。

2.现实世界中可能没有许多LR-HR成对的数据，比如说有些设备采集到的最高分辨率有限，如果还想利用超分辨率来获得更高分辨率的图像，就没有HR的图像。并且许多LR图像也不清楚是通过何种方法从HR图像退化而来，有时候甚至HR图像和LR的图像的分布都有所不同，这就导致了许多算法的精度非常有限。

本文为了解决上述的两个问题，提出了一种双重网络来解决，通过形成一个个闭环的训练过程来缩小映射空间，并且仅仅通过LR图像来学习LR->HR的映射关系，对于一些真实场景中的数据也能够很好地适应，达到很好地性能。

1 介绍

基于深度网络的SR方法已经有了很好地发展，但是还是存在问题，说白了还是上一部分那两个问题。
本文的贡献原文中分了三部分来陈述，实际上也就是提出了这个闭环的双重网络来完成SR任务。其它的贡献就是一些相关的实验，包括理论分析这个网络的优势以及有成对LR-HR数据的实验和仅有LR数据的实验。

2 相关工作

有监督的SR

基于插值、基于重建、基于学习

无监督的SR

主要是一些融合了GAN的方法，如CinCGAN等。

双重学习方法

这种方法包含一种主要的模型和第二重的模型（也就是两个模型），自动学习两个不同的模型来增强最后的推理结果。如DualGAN等等。

3 提出的方法

整个双重回归的方法如下图所示：

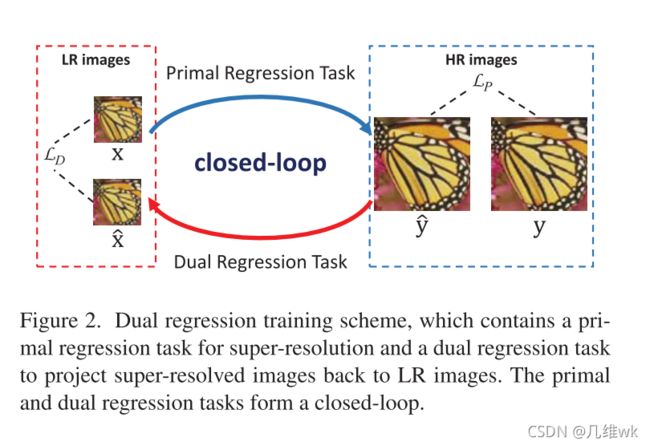
这个图也就是这篇文章的核心的创新之处，之前用深度学习做SR任务的只有Primal Regression Task，也就导致了前面提到的不适定问题的出现。本文有加了个Dual Regression Task，这就等于在原有的LR—>HR的映射变成了LR<—>HR，多增加了一个限制，使得SR效果更好。

3.1 处理成对的数据

先解释下，所谓成对的数据就是有对应LR的HR图像的数据。不成对的数据就是只有LR，没有HR，也就是没有label或者说没有ground truth。那么处理成对的数据现有的方法都是直接那HR当label，来训练一个深度模型完成SR任务，而本文将SR任务分为两个：
1.Primal Regression Task：寻找函数P，使得P(x)相似于HR图像y，也就是y ~ P(x)。P就是X到Y的一种映射。
2.Dual Regression Task：再寻找函数D，使得D(P(x))相似于LR图像x，也就是x ~ D(P(x))。D就是Y到X的一种映射。
这样D和P也就构成了一个闭环，如果P(x)更加接近于真正的HR图像，那么D(P(x))也就你应该更加接近于真正的LR图像。这样一约束，训练出来的P映射也就更好。
简单来说就是在最后的损失中增加D映射的损失，从而使训练出来的P映射更好。整个训练的过程也就是下面的损失函数。这个函数很好理解，这个$\lambda$怎么取后文中有分析。

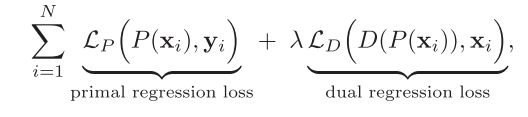
稍微详细解释一下，根据原文的说法，这里面的$L_P$和$L_D$是带有正则项的1范数损失，详细写成公式是下面这样：
$L_P(P(x_i),y_i)=||P(x_i)-y_i|{|}_1+\alpha ||{\omega }_P|{|}_1$
$L_D(D(P(x_i)),x_i)=||D(P(x_i))-x_i|{|}_1+\alpha ||{\omega }_D|{|}_1$
这两个式子中，前半部分就是1范数，后面的一项就是$L1$正则化项，${\omega }_P$和${\omega }_D$是网络整体的参数，$\alpha$是正则化系数，加了这个惩罚项就会很好地防止产生过拟合的现象。
这里作者提到，也可以在HR域内再加个限制，也就是对HR图像下采样再上采样重建回去，得到的图像应该越接近于原来的HR图像越好，这样就能够让D函数训练的更好，也就让P函数训练的更好。这样做的问题就是会增加算法复杂度。作者强调他增加D这一环节以达到闭环并不会增加多少计算代价，所以他最后选择了这种结构。

3.2 处理不成对的数据

处理自然场景下的数据时，一般是只有LR数据而没有HR数据的，这个时候就不知道LR数据是如何从HR退化而来的，就涉及到了不适定的问题，解决起来十分具有挑战性。
训练的算法如下：

这个算法表格乍一看挺唬人的，其实就和正常的深度学习模型没啥区别，只不过这里面用到了两种数据，一种是我们这节提到的不成对的自然数据，也就是$S_U$，还有就是成对的数据，但这个成对的数据不是真正的成对数据，而是synthetic的数据，也就是合成的数据，就比如我现在有一个LR的图像，我没有它真正的HR图像，我可以通过一些插值方法比如双三次插值等等的方法，来对这个LR图像进行插值，这样就得到了一个合成的HR图像，也就有了成对的数据，这些数据记作$S_P$。$S_U$总数为$M$，每个batch的数量为$m$,$S_P$总数为$N$，每个batch的数量为$n$。在训练的过程中，实际上还是用到前面的那个损失函数，只不过在这个算法的表格里作者写的更细一点。在更新$P$时，因为前面损失函数中的两项中都有$P$，所以就都用到，只不过在没有成对图像时，第一项也就是：

就没有了，因为没有$y_i$。如果有成对数据，就两项都有。第一项有没有就是由算法表格中提到的哪个Indicator function来决定的。更新$D$时只用到第二项，所以损失函数只有第二项。
说来说去，其实还是那个损失函数，没有一丝丝改变，变的只是我可以输入没有ground truth的数据来训练，只要把损失函数的第一项去掉就可以了，也可以让网络的参数得到优化，最终实现SR的任务。

3.3 训练方法

训练的方法前面都说的差不多了，这里就说了下作者用到的的成对数据和合成不成对数据的比率$\rho$，如下：
$\rho =m/(m+n)$
$m$是不成对数据的数量，$n$是合成不成对数据的数量，也就是$\rho$就是不成对数据占总数据的比率。作者发现$\rho =30\%$时结果最好。

3.4 与基于CycleGAN的SR方法的不同之处

首先要声明一下，我没有读过CycleGAN的原文，但我对GAN网络还是有一定了解的。这里作者把DRN和基于CycleGAN的方法进行对比，主要有两个方面的优势。
第一，CycleGAN是采用一个叫循环一致性损失来避免模式溢出的问题。啥叫模式溢出呢？我理解的大概意思就是GAN网络本来是网络的一个“创作”过程，用GAN网络训练出的SR模型它的生成器就会生成让判别器误认为是SR图像的图像，这个生成的图像可能是SR图像，但可能不是原来的LR图像对应的SR图像，那怎么办？就加个循环一致性损失来限制它，让它生成的SR图像尽量能和LR图像去对应，所以这个损失函数就非常关键，设计好这个损失就能提高SR的性能。而DRN不一样，它没用GAN，而是直接加了一个额外的限制，也就是前面提到的不仅从LR到HR我要监督，反过来HR到LR我也要监督，这两个过程都有损失，不成对的数据就后面这个过程单独有损失，这样多加了一个反过来的过程，而且不用GAN，网络结构和训练过程都简单了但效果却提高了。
第二，CycleGAN没有用到合成的成对数据（据我推测CycleGAN应该是直接就用不成对的数据进行训练），而DRN训练时综合了不成对和合成的成对数据，增强了训练过程。

4 更多细节

4.1 DRN结构

说到结构就直接上图吧：

整体结构就是经典的U-net结构，就是在右边加了一个回来的支路，也就是。其中RCAB的结构如下：

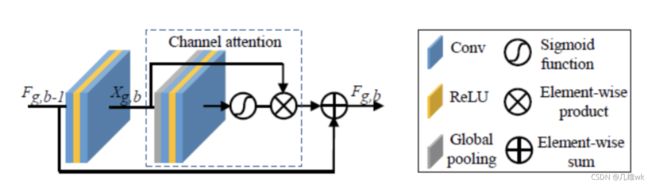
这个也就是在原本的残差块中增加了通道注意力。
文中提到在上采样时，会增加一些不同尺度的输出，就是结构图中对应的1x image, 2x image，并且原文还说这些输出也可以用来计算loss，用来网络训练。但是有一个问题，具体是怎样计算呢？尺度都不一样，而且计算出来最后怎么组合到最终的损失中呢？这里原文没有说得很清楚，我猜测是不同尺寸的图像时通过插值调成同样的尺寸从而来计算loss，最终可能就是把所有的loss加到一起来组合所有的loss。

4.2 理论分析

这一部分就有些晦涩难懂了，主要就是理论的分析了为啥作者的模型比较好，用到了Radeacher复杂度这个东西，我能理解到的就是最后通过给出的定理证明除了本文方法的函数空间更小，相比其它传统的深度SR模型更有优势。由于这部分的内容不是重点，所以我们有深入研究这些定理。

5 实验

5.1 有监督的结果

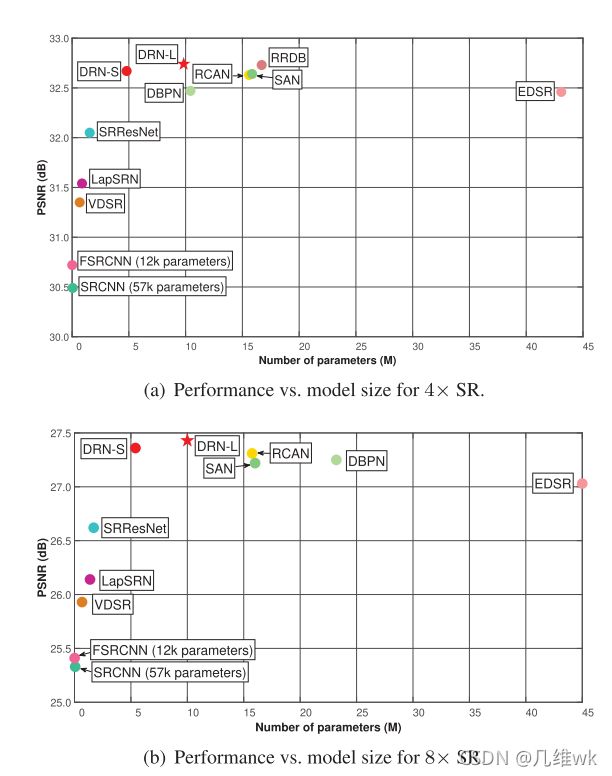这里作者又提出了两个模型，DRN-S是小一点的模型（参数少一点），DRN-L是大一点的模型（参数多一点，DRN-S和DRN-L具体简化或者复杂在哪里，可以参看源码）。这个结果图中纵坐标表示PSNR，这个值越大越好，越大表示得到的SR图像的质量越高。横坐标是参数量，这个值肯定是越小越好，因为参数越少推理速度越快。所以总的来说，越靠近这个图的左上角的网络性能是越好的，所以本文的方法比较好。

5.2 数据集和实现细节

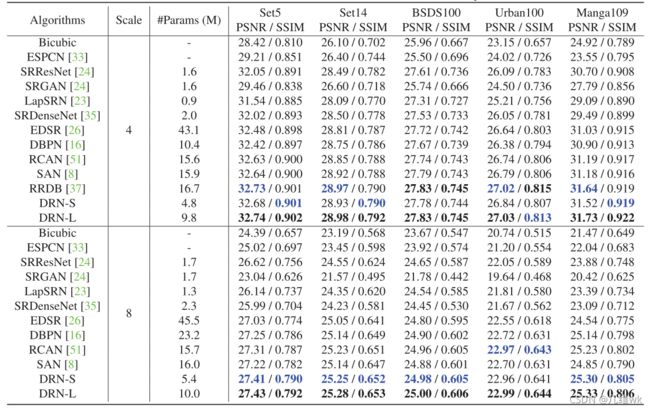
作者是在SET5,SET14,BSDS100,URBAN100和MANGA109这几个数据集比较的不同方法的性能，评价指标用的就是PSNR和SSIM，训练的时候实在DIV2K和Flickr2K上进行的训练。

5.2.1 与最好方法的比较

5.3 在不成对数据上的结果

作者还把这个方法应用在大量的真实世界中的不成对的数据上。但是对于真是世界中的数据进行评价几十个问题，因为没有参考的HR图像，无法计算PSNR和SSIM。作者通过使用不同的退化方法对原图进行下采样获得LR图像，从而获得合成的成对数据，并在这上面进行评价。

5.3.1 数据集和实现细节

作者随机从ImageNet中选出了3K张图像，称之为ImageNet3K，通过不同的退化方法（文中提到最邻近和BD方法）下采样从而获得LR图像，这个图像就看做不成对的数据，虽然是不成对的自然场景中的数据，但是这个图像的原图是HR的，这样就可以进行PSNR和SSIM的计算。而合成的成对数据则是采用DIV2K的数据集进行双三次插值来获得。在视频任务上，作者收集了3K帧原始视频帧作为不成对的数据取取训练模型。
看完上面这段，你可能有点凌乱，总结一下：
1.训练时用到两种数据：成对和不成对的数据；
2.成对数据中包含HR图像和LR图像，LR图像是DIV2K中的原始图像，HR图像是经过DIV2K中原始图像双三次插值得到的，训练时LR图像和HR图像都要用到；
3.不成对数据中也包含HR图像和LR图像，HR图像就是从ImageNet中随机抽取的3K张原图，LR图像则是对HR进行某种下采样得到的训练时只用到LR图像。
在这一部分作者使用了DRN-S来进行评价，在对比时记作DRN-Adapt。

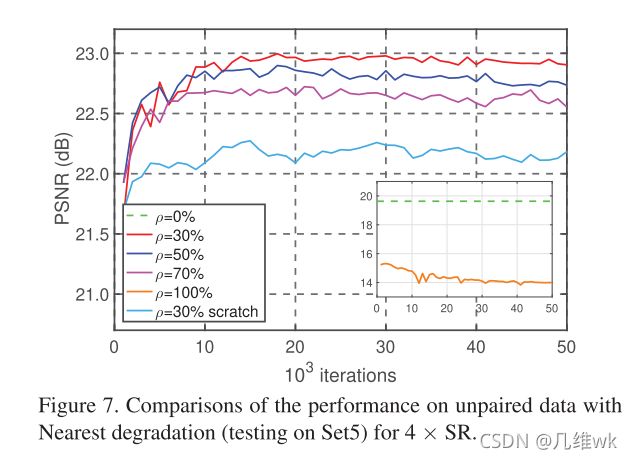
5.3.2 在不成对数据上的比较

这里在SET5,SET14,BSDS100,URBAN100和MANGA109这些数据集上比较时，其实输入DRN的LR图像是经过这些数据集原图通过Nearest或BD退化得到的，然后经过DRN得到的SR图像再和原图像计算PSNR和SSIM。使用Nearest退化时，还和使用Nearest插值的方法进行了比较。

5.3.3 在真实场景中不成对数据上的比较

6 更进一步的实验

6.1 消融实验

这个实验主要是为了证明Dual结构比较有用。

6.2 $\lambda$对DRN的影响

之前的损失函数里面不是有个$\lambda$吗，作者做了实验来看这个值取多少合适。

6.3 $\rho$的影响

7 结论

结论就是作者提出个新的Dual regression结构 对于成对和不成对的数据进行超分辨率任务，在做了许多实验之后证明了这个方法还是优于其它方法的。