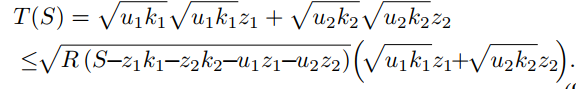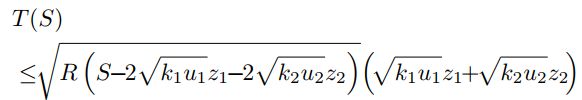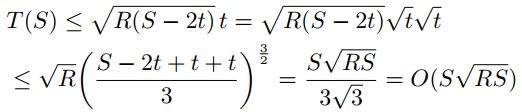论文笔记 -- Communication Lower Bound in Convolution Accelerators 卷积加速器中的通信下界

论文笔记 – Communication Lower Bound in Convolution Accelerators 卷积加速器中的通信下界

@(论文笔记)

声明：
本文是对计算机体系结构领域的旗舰会议 HPCA 2020论文：
Chen X , Han Y , Wang Y . Communication Lower Bound in Convolution Accelerators[J]. 2019." 的详细解读。
部分内容参考：北京智源人工智能研究院 微信公众号
文章链接：https://arxiv.org/abs/1911.05662v3

1. 目的

在当前的卷积神经网络(CNN)加速器中，内存访问主导能源消耗。

图一是Eyeriss的统计结果，显示能量消耗最大的部分在寄存器，这是因为Eyeriss是一个脉动阵列，片上数据传输非常频繁。第二个图片来自陈云霁论文的数据（Diannao)，显示片外访存几乎占了所有能耗，所以现在CNN加速器访存仍然是性能瓶颈。

通常，外部DRAM的访存比算术单元（乘加）的功耗要高出2-3个数量级，且DRAM访存功耗会占到**90%左右的总功耗。而对于功耗的片上部分来说，内部Reg的功耗占据了50%**以上，算术单元只占20%不到。

一般使用数据复用可以有效减少访存次数。而数据复用高度依赖数据流设计，数据流设计有下面几种方法：

1. 为某些网络设计一个精细的专用的数据流
2. 从某些待选数据流中选择一个当前网络最适配的数据流
3. design space exploration (DSE)设计空间探索
   但是以上方法中有些论文并没有抓住主要矛盾（访存）来优化，并且大部分工作在设计数据流时采用的是一种启发式的方法，因此并不能保证得到的结果是最优的。所以该文主张从卷积操作的通信理论下界作为最优标准，来衡量加速器的访存性能。

如果说有足够大的片内存储，就可以保证pe做卷积操作时所有类型的数据（input,weight,output)都只需要访存一次，这肯定是单层的访存最优值。但是该前提一般是不成立的。因为没有那么多内部存储，而且根据不同应用，需要的内部存储大小也不同。针对这些问题，该文主要做了如下主要工作：

• 解决了CNN加速器中的一个基本问题:如果一个卷积层是在只有有限的片内存储的CNN加速器上实现的，那么该层的片外通信的下界是什么。该文作者对这个问题进行了数学推导。
• 证明了卷积只比矩阵乘法(MMs)多一级数据重用(滑动窗口重用)。基于这一结论，设计了一个融合滑动窗口复用的数据流和一个通信最优的MM实现，以最小化芯片外通信。
• 设计了一种负载和存储映射机制，可以让片内buffer和reg的通信接近理论下界。
• 提出了一种通信最优的CNN加速器结构，它不仅能达到最小通信，而且能适应不同卷积层维数，资源利用率高。

2. 背景

2.1 卷积循环以及复用方法

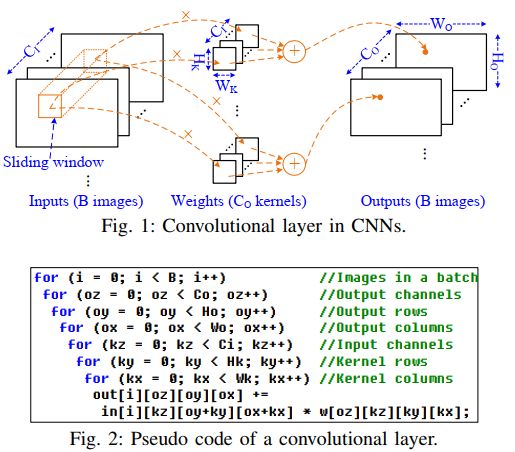
首先给出了卷积的伪代码，如下图，最外层是batch，然后是输出像素，内层是卷积核的三个维度。（假设stride=1)

上面的循环有7层，直接通过这个来搜索最优的通信方法是困难的，因为其设计空间非常大，需要考虑不同的循环顺序，循环展开以及分块方法。 此外，诸多的数据复用方法的组合可以构成非常复杂的数据流： + **InR**，**输入复用**，输入被多个卷积核重用 + **WndR**，**滑动窗复用**，一般卷积stride都不会太大，所以两次卷积之间重叠的那部分输入数据可以复用 + **WtR**，**权重复用**，一个权重一次导入可以跟多个不同的输入做计算 + **OutR**，**输出复用**，一个卷积输出像素直到它被计算完整（遍历完所有输入通道）之前一直驻留在片内存储中

2.2 相关工作的局限

a. 单一数据流方法

该文作者值出，目前很多数据流都旨在优化性能，带宽等，（具体指哪些论文可以看原文）但他们很多都基于一种启发式的分析方法，也就是说他们虽然都强调了其加速器的优越性，但没能解释为什么他们的是最优的。因此这种方法并不能保证其数据流是最优的。
而目前为止在讨论片上片外访存通信方面SOTA的论文Eyeriss也被该文作者指出无论其片外还是片内通信都不是最小的。

b. 多数据流方法

此外，对于一些使用多种数据流的工作，虽然相比于单一数据流能由很大的适应性，但其也只能保证在所选的几种数据流中某种是最优的，但并不能找到真正的最优架构。

c. 设计空间探索方法

为了找到一个明确的优化目标，一种方式是遍历所有的循环次序以及分块参数等，也就是设计空间探索(DSE)。但是即使只考虑一种非常简化的只有两层循环的情况，也需要遍历10的13次方的空间，这使得遍历搜索空间变得不现实。启发式的搜索方法也只能找到局部的最优解。

d. 其他工作

也有其他工作考虑优化fuesd-layer的问题，也就是多层的联合最优，但是还没有人彻底地分析过单层的通信最优问题。有论文研究了所有输入和权重只从片外访存一次的情况，但得到的结果是片内buffer需要非常巨大（从几兆到几百兆）。

2.3 准备工作：红蓝卵石游戏（Red-blue Pebble Game）

该文指出，片外访存的通信下界非常依赖1981年提出的一种红蓝卵石游戏:

tlong, Jia-Wei and 1I. T. Kung,“I/0 COMPLEXITY: THE RED-BLUE PEBBLE GAME”

这是一个研究两层存储之间最小通信次数的理论模型。下面引用其中的一个定理，也是该文的起源理论。

基本模型假设：

1. 存储层次由一个无限制的快mem和一个无限制的慢mem组成，对于该文而言，慢mem对于片外DRAM，快men对于片内存储（SRAM和Regs）。
2. 某种算法可以组织为有向无环图（DAG），在这个图中，每个节点表示一种数据输入或操作（这个操作处理输入数据并得出输出结果）。每条边表示数据操作节点之间的依赖关系。

红蓝卵石游戏论文中提出一种S-partition的有向无环图分割模型，这种模型可以有效描述很多计算图问题（比如FFT,矩阵乘法），该文将其引申到了卷积操作，S-partition具体描述如下：

设$G(V,E)$为某一算法的有向无环图表示。$V$代表点集，$E$代表边集。如果图$G$的一种分割方式满足下面几个性质，那么就将这种方式称为$S-partition$.


性质1：$V$（顶点集）被分割到$h$个子集中$V_1,V_2,\cdots ,V_h$，并且保证各个子集之间没有交集，且他们的并集就是$V$。
性质2：各个子集之内也不存在循环相依性。
性质3：对于任意一个$V_i$，都存在一个支配集$D_i$，并且$|D_i|\le S$。支配集表示如果该集合之外的任意一个点，都有$D$中的某一个点，使得他们之间的边存在于边集$E$中。
性质4：对于任意一个$V_i$，输出集$O_i$满足$|O_i|\le S$.其中输出集表示$O_i$中的节点在$V_i$中找不到后继节点。

对于所有$S-partition$分割后的DAG，都对应一个分割后的子集个数。而$P(S)$表示任意一种$S-partition$的子集个数最小值。
下面直接给出"I/0 COMPLEXITY: THE RED-BLUE PEBBLE GAME"论文得到的结论：

定理1.给定一个容量为S的快mem，以及一个可以用DAG描述的算法，其完成该算法需要的快慢两层mem之间的最小通信次数Q满足：
$$Q\ge S\cdot (P(2S)-1).$$

3. 逐层计算时片外访存的下界

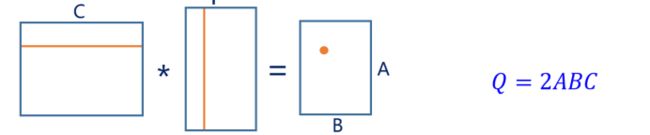
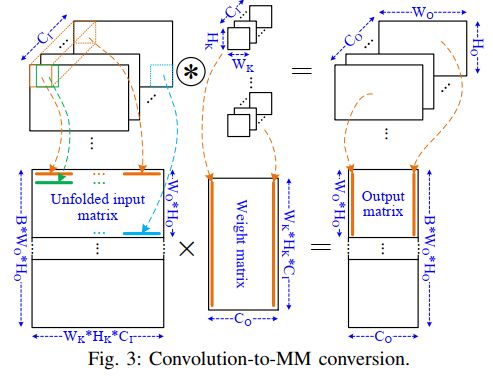
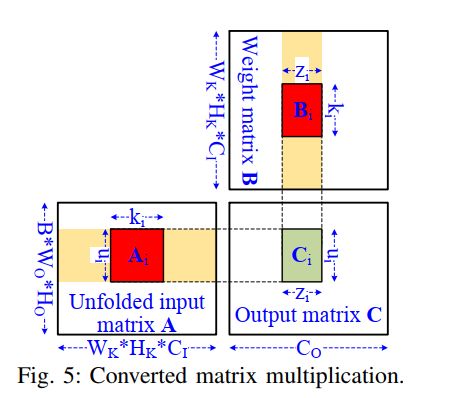
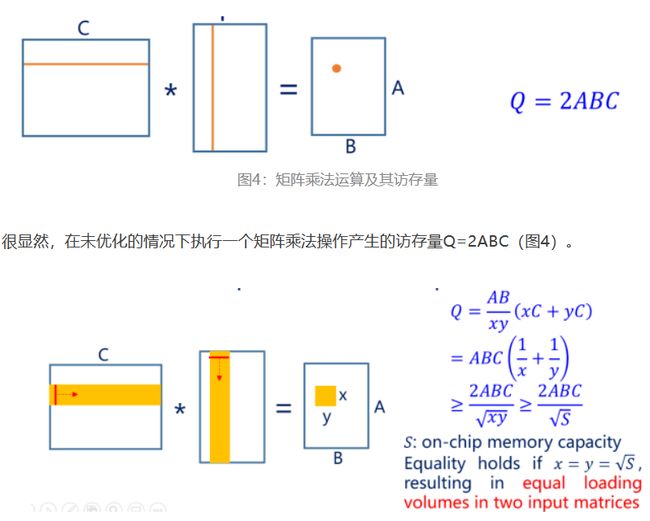
首先，卷积层可以转化为矩阵乘法。如下图所示：

简单来说，就是把每一次卷积核要跟输入乘累加的那部分输入拉成一行，得到的输出进行重组之后就是输出map。
但是这种转换只是逻辑等价的，或者说仅对于权重和输出来讲是等价的，这只是对它们的元素做了一下形状的重塑，没有增加或删除元素。但是对输入则不一样，我们将卷积窗展开了。卷积窗中有重叠的元素可以重用，按上面的转变方式这种重用就会消失。

实际上，其他复用方式在MM中都体现了，比如InR,每行输入实际上都会被多行weight使用，或者WtR,每列权重也会被多行输入使用。OutR则发生在一次算不完整个MM的时候，可能要把输入行分成几部分算，这时候就要引入OutR.所以，虽然卷积有7层循环，但其实它只比矩阵乘法多了一种复用方式，也就是WndR。
为了等效地将卷积转为MM，引入了一个参数R:

来表示每个输入像素被复用的最大次数。（比如卷积核3*3,D=1时，除了输入图外面一圈外，复用最大次数为9次）

此外，当$R=1$时，卷积就跟矩阵乘完全等效，又因为FC层实际上也是矩阵乘，所以也可以等效为R=1时的卷积。

PS: Convolution-to-MM转换只是用于推导的一个逻辑操作。在这篇文章的数据流或架构中不是一个真正的操作。

3.1 理论推导

首先假设加速器的工作方式是逐层计算的，并且片内的memory无法满足只从片外读取一次数据的要求（不够大）。

3.1.1 引理一

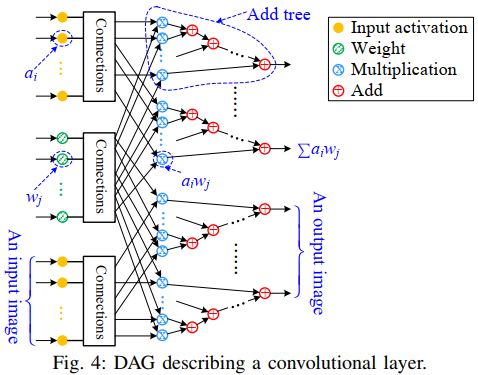
引理一：如果卷积层用DAG（有向无环图）表示，则DAG中内部和输出节点的个数为$2B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I$。

证明可以看下图：下图是卷积的DAG表示，可以看到分为三个层次，分别是输入节点，乘法节点以及加法节点。上面这个式子表示的是中间节点以及输出节点的个数，“2”表示乘加单元算两个节点。输入节点到乘法节点的连接关系我们并不需要关注，它肯定是按照卷积的顺序将输入进行排列的。
此外，图中每个乘法单元都输出一个乘积项（term),加法树用来累加这些项并得到最后的输出和。

个人理解：
卷积计算图的S-partition的分割问题实际上就是加速器做的事情。S-partition将整个卷积计算分解为若干个不重叠的部分，每一部分都对应一次加速器中的映射。红蓝卵石模型已经给出了某种图算法在快慢Mem两级结构中的IO复杂度，因此就可以把卷积在加速器里的实现转换到该模型来求解。而片上存储$S$的限制主要作用在分割后的图中的节点数目上，因为分割后的图中所有节点都需要在片内完成，存储自然不会超过$S$，而S-partition中对应这部分的描述实际上就是支配集，支配集的概念是其外的所有节点都有边连接到支配集中的某些点，而支配集中的点就是需要存储的信息（大部分是），所以其数量也不应该超过$S$。而S-partition的最后一条性质，输出节点数小于S，这个也比较好理解，如果说某种S分割后某个子集正好包含了$S$个输出节点，那么其也满足支配集元素数小于S，所以这种情况就是存储都用来存输出节点，也满足条件，所以显然分割后所有子集的输出节点数不会大于$S$.

3.1.2 引理二

引理二：设片上存储单元个数以及加法树个数都不超过$S$,$T(S)$表示用上面这些资源最多可以产生的乘积项数（term）。对于一个滑动窗复用度为$R$的卷积层，有$T(S)=O(S\sqrt{RS})$.

证明： 基于卷积核MM的关系而来。首先使用$A,B,C$分别表示展开为矩阵后的卷积input，weight，以及output张量。那么将有$AB=C$.其中，使用不超过S的片上存储计算得到的乘积项可以分布在$C$中的任意位置。由于$C$中的元素是很多乘积项之和，所以上面S容量的片上存储，其实也隐含了加法器个数最大是S个（当所有容量都用来存输出时可以取到）。计算出来的乘积项可能分布在C中不同的元素内部，或者说乘积项可以分布在若干个不同的加法树中，他这里用了一个词叫overlap in C，因该是指算出来的乘积项可能有些会落在同一个输出点内，因此乘积项相对C来说有overlap。
首先我们来证明，如果要最大化乘积项个数，那么所有乘积项必须来自一个块（block），或者说这些项可以形成一个block.
这个理论从直观上就可以说明，比如说我现在需要得到10个乘积项，但是我的存储资源是受限的，现在我又知道，乘积项一定是通过A和B中的元素相乘来的，如果说要得到10个项，那必定要有10个元素相乘，而如果从A中随便拿10个，B中随便拿10个，那就需要20个存储空间，显然不是最优的，最优情况下应该是A中只出1个元素，然后跟B中不同的10个元素相乘得到10个积项，也就是最大化复用，而这种方式出来的这10个乘积项，无论如何在输出矩阵中都是处于同一行的，如下图，即使B中的这些点分散在不同的列中，也可以通过重组把他们合并到相邻的列。

上面只是从直觉角度简单说明了理由，论文中有详细的理论推导：
不失一般性地，考虑$C$中的两个不重叠的矩形块$C1,C2$.块$C_i$的大小表示为$u_i\times z_i$，最小为1*1.每个输出块都是A和B中的矩形块矩阵乘而来，这里将生成$C_i$的$A_i,B_i$大小表示为$u_i\times k_i$以及$k_i\times z_i$。 其中$A_1,A_2$或$B_1,B_2$都可以是重叠的，但不能同时重叠，否则$C_1,C_2$也会重叠。则$T(S)$可以表示为：
$$T(S)=u_1{k}_1{z}_1+u_2{k}_2{z}_2$$
下面分两种情况讨论：
第一种：假设$A_i,B_i$都没有重叠，则由于片上存储容量$S$大小的限制，有如下约束：
$$\frac{u_1{k}_1}{R}+\frac{u_2{k}_2}{R}+z_1{k}_1+z_2{k}_2+u_1{z}_1+u_2{z}_2\le S$$
上式左边两项表示考虑WndR复用后输入实际需要导入的元素个数。由均值不等式，可以得到：
$$\frac{u_i{k}_i}{R}+z_i{k}_i+u_i{z}_i\ge \frac{3}{\sqrt[3]{R}}(u_i{k}_i{z}_i{)}^{\frac{2}{3}}$$
当且仅当$\frac{u_i{k}_i}{R}=z_i{k}_i=u_i{z}_i$时等号成立。
结合上面两个式子可以得到：
$$(u_1{k}_1{z}_1{)}^{\frac{2}{3}}+(u_2{k}_2{z}_2{)}^{\frac{2}{3}}\le \frac{S\sqrt[3]{R}}{3}$$
如果令$t_i=(u_i{k}_i{z}_i{)}^{\frac{2}{3}}$,那么$T(S)=t_1^{\frac{2}{3}}+t_2^{\frac{2}{3}}$且$t_1+t_2\le \frac{S\sqrt[3]{R}}{3}$。要求$T(S)$最大值，由于其严格凸并且连续，其最大值在限定范围的边界取得，也就是其中一个为$\frac{S\sqrt[3]{R}}{3}$，另一个为0.此时$T(S)$最大值为$\frac{S\sqrt{RS}}{3\sqrt{3}}=O(S\sqrt{RS})$，从这里就可以看出，要取得最大值，$C1,C2$中有一个为空，说明只有一个block。

第二种：假设$A_i,B_i$有重叠，这边假设$A_1,A_2$有重叠，$B_1,B_2$没有重叠。则有如下约束：
$$\begin{gathered} \frac{u_1{k}_1}{R}+z_1{k}_1+z_2{k}_2+u_1{z}_1+u_2{z}_2\le S \\ \frac{u_2{k}_2}{R}+z_1{k}_1+z_2{k}_2+u_1{z}_1+u_2{z}_2\le S \end{gathered}$$
也可以写成：
$$\begin{gathered} u_1{k}_1\le R(S-z_1{k}_1-z_2{k}_2-u_1{z}_1-u_2{z}_2) \\ {u}_2{k}_2\le R(S-z_1{k}_1-z_2{k}_2-u_1{z}_1-u_2{z}_2) \end{gathered}$$
那么：

由基本不等式可以得到：$z_ik_i+u_iz_i\geq 2\sqrt{k_iu_i}z_i$，则：

等号只在$k_i=u_i$时成立。令$t=\sqrt{k_1u_1}z_1+\sqrt{k_2u_2}z_2$，则有：

最后一个等号在$t=\frac{S}{3}$时成立。反过来看推导过程，可以令$k_1=k_2=u_1=u_2$以及$z_1+z_2=\frac{\sqrt{S}}{\sqrt{3R}}$时，$T(S)$取到最大值。这个关系表示$A_1,A_2$一样大，且他们是交叠的，所以实际上得到的$C_1,C_2$都落在$C$中大小范围为$u_i$的行内，又因为$z_1+z_2=\frac{\sqrt{S}}{\sqrt{3R}}$，也就是说虽然$B_1,B_2$是不交叠的，也就是两块来自不同列，每一列实际上表示的不同的输出通道，而输出通道实际上对顺序不敏感，也就是说在输出$C$和$B$图中可以任意调换列的位置。所以这个条件表示两个块$C_1,C_2$的宽度之和是固定的，所以可以将两个block合并为1个。

结论：
上面两种情况都推导出了$T(S)$最大时，片内只存在一个单独整块$C_1$，并且$u_i,z_i$的关系应该满足$u_i=R{z}_i$，$T(S)=O(S\sqrt{RS})$。

---

个人理解：
上面的通过反证法，证明了这样一个问题：
如果把乘积项对应在$C$中psum存到大小为$S$的片内存储里，这些乘积项的输入和权重也存进去，那么获得最大数量的乘积项时，他们对应在$C$中应该能组织成一个稠密的块，而不会是分散开来的。
通过反证法，首先假设乘积项在$C$中的分布在一个单独的块$C_1$，它对应的乘积项个数为$T(S)$。假设存在另外一个游离于该单独块的小块（甚至一个点）$C_2$，在相同约束条件下，$C_1,C_2$的联合对应的乘积项个数$T(S{)}^{\prime }$比$T(S)$要大。
然后通过上面的证明，得到的结果是当两个块的联合对应的乘积项个数$T(S{)}^{\prime }$最大时，发现$C_2$要么就是为空集，要么就是可以跟$C_1$合并变成一个整块。由此推翻了原假设。说明对于固定容量$S$的存储，$C$中不存在这样一个游离块，使得两块联合后得到更多的项。

---

3.1.3 引理三

引理三：假设中$V_1,V_2,\cdots ,V_h$是卷积层DAG的S-partition分割后的子集，则每个子集最多包含$2T(S)+S$个内部和输出节点。
证明：
首先，由性质4，任意$V_i$的输出集最多由S个节点，也表示其最多只能涵盖S个加法器树中的某些节点。
其次，由性质3，任意$V_i$都有一个支配集$D_i$，并且其元素个数不大于S。由$T(S)$的定义，其表示利用最多S容量的内存（加法树）最多能产生的乘积项，则支配集中最多有$T(S)$个乘积项，他们被分配最多$T(S)$个加法树中。
则$V_i$中最多包含的内部和输出节点为2T(S)+S个。
下面解释下这个最多节点数是怎么算的。首先，节点数并不等于内存容量S，因为psum是一个中间过程值，只要属于同一个加法树都可以用同一个存储单元来存。所以$V_i$最多包含的存储单元就是$S$，表示$S$个加法树的输出或某个中间节点。$2T(S)$的来源则是$V_i$中的支配集$D_i$最多包含$T(S)$个乘积项节点，这些节点可以分布在$S$个加法树中，没分布到的加法树则可以贡献其最终输出节点。而每个乘积项节点都会对应一个加法节点，所以有$2T(S)$。
结论：
卷积层DAG的S-partition分割后的每个子集都最多包含了$2T(S)+S$个内部和输出节点。

3.2 卷积通信下界推导

回顾之前定义的S-partition分割问题，$P(S)$表示的是对于任意S-partition分割，其至少包含的子集个数。而现在引理1告诉我们：卷积DAG图包含的内部和输出节点个数为$2B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I$，引理3告诉我们卷积层DAG的S-partition分割后的每个子集都最多包含了$2T(S)+S$个内部和输出节点。那么很显然：
$$P(S)=\frac{2B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I}{2T(S)+S}=\frac{2B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I}{2\frac{S\sqrt{RS}}{3\sqrt{3}}+S}$$
一般来说$\sqrt{RS}>>1$，所以上式分母上的S可以忽略。得到：
$$P(S)=\Omega (\frac{B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I}{S\sqrt{RS}})$$

得到了$P(S)$根据定理1:
$$Q\ge S(P(2S)-1)=\frac{B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I}{2\frac{\sqrt{2RS}}{3\sqrt{3}}+1}$$
即可求得卷积通信下界：

$$Q_{DRAM}=\Omega (\frac{B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_I}{\sqrt{RS}})$$

需要注意的是，上面的通信下界结果是采用$\Omega$表示的，它表示当卷积规模足够大时，片外与片内存储容量的通信的一种渐近关系。所以不排除当工作负载比较小（卷积规模很小）时，会有该下界值不匹配的情况。

---

个人理解：
首先盗一张图：

这张图展示了矩阵乘法在考虑片上容量$S$限制以及进行分块时的通信下界。可以发现，卷积计算相对于矩阵乘法在通信下界上其实只是在分母上多了一个$\sqrt{R}$，其含义就是两者的唯一区别就在于卷积由滑动窗复用WndR。

4. 访存通信优化的数据流

4.1 最小化片外访存的数据流

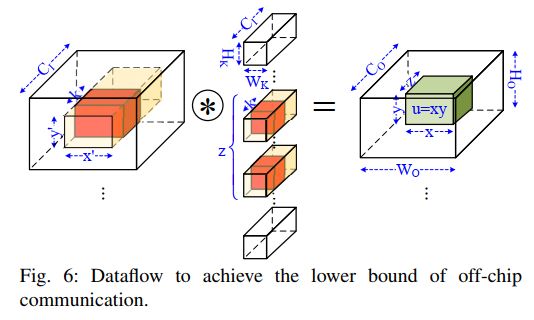
最小化片外访存的数据流是根据上一节中的引理二的推导过程得到的。具体数据流如下图所示：

输出矩阵$C$被划分为等大小的$u\times z$块，块大小需要满足$u \approx Rz$(根据引理二中的推导)并且需要满足片上存储容量的限制。所需要的输入和权重数据如图中黄色部分所示。输入矩阵的大小为$x'\times y'$，其中$x'=x +W_k-1 and y' =y+H_K-1 (D=1)$,其展开后就对应了图5中的矩阵形式。

此外，如果输出通道比较小（$W_o{H}_o<xy$)，那么将考虑利用batch中的另外的feature对应的output map拼接上去。则此时有$u=bxy$

由于片上存储的限制，黄色部分的数据可能无法一次性读入，因此需要进行分批，这里设定一个参数$k$,表示一次读入的通道数，也就是图中橙色的部分，每次都读入这样一个小块，然后计算得到对应的输出的部分结果（文中称为sub-matrix），这样不停地顺序读入输入小块，并将结果sub-matrix逐次累加，输入完所有黄色部分后就得到了输出矩阵，此时再输出到片外。通过这种方式，输出所需要的权重和输入实际上都只读了一次。当然，这里的只读了一次只是相对于一个输出块$bxy$而言的，因为考虑多个块实际上相同 的输入和权重还是会被重复读入。
下面是这个过程的伪代码：

对于这样一个数据流，五元组$\{b,z,y,x,k\}$唯一确定了一套数据调度方式，此处实际上$k$不影响片外访存，因为$k$实际上受到片内存储量的影响，如果k比较小，则为了利用完片内存储，$xy$将会扩大，片内存储几乎全部分给输出。因此理想化时$k=1$，此时导致用来装载输入数据的片上存储最小。

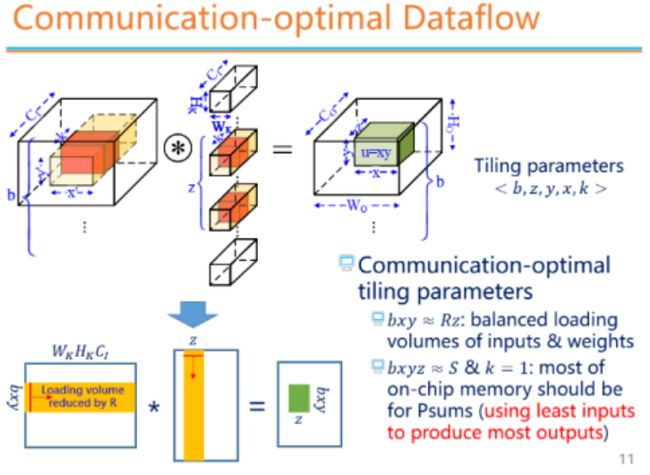
上图更直观地展现了分块操作对应到矩阵角度是如何实现的。因为卷积窗的重用，每个元素最多可以被重用R次，使得输入矩阵实际读入的数据就被减少到了最多$1/R$。以上推导过程可以得到两条选择分块参数的原则：

1. $bxy\approx Rz$，即从两个矩阵当中读入的量相等；
2. $bxyz\approx S且k=1$，即要把几乎片上所有存储全部分配给输出部分，这样可以以每次最少的输入产生最多的输出，这样做其实和矩阵乘是类似的。

这两条原则在下面的推导中有解释。

下面从数据复用角度分析一下这种数据流的优点：

• OutR: 完全利用，因为输出直到计算完毕都驻留再片内。
• WndR: 完全利用，每个输入都会被重用最多$R$次。
• InR: 部分利用，输入实际上被$z$个kernel复用。
• WtR: 部分利用，一个权重被$b\times x\times y$个输入复用。（这点从上面的矩阵角度很容易看出来）
• 充分利用OutR和WndR，同时平衡地结合InR和WtR。

下面文章从理论角度推导了该数据流方式能够逼近通信下界的原因：
首先有如下推论：

• 输出图中总共有$\frac{B{W}_O{H}_O{C}_O}{bxyz}$个blocks
• 对于每个block，需要的权重和输入数分别为$W_K{H}_K{C}_{1}z$和$b{x}^{\prime }{y}^{\prime }{C}_1$

则可以得到DRAM访存可以分为两部分：
$$\begin{gathered} Q_{read}=\frac{B{W}_O{H}_O{C}_O}{bxyz}(W_K{H}_K{C}_{1}z+b{x}^{\prime }{y}^{\prime }{C}_1) \\ \approx \frac{B{W}_O{H}_O{C}_O}{bxyz}(W_K{H}_K{C}_{1}z+\frac{W_K{H}_{K}bxy{C}_1}{R}) \\ {Q}_{write}=B{W}_O{H}_O{C}_O \end{gathered}$$

此处约等于是建立在$R\approx \frac{W_K{H}_K}{D^2},x^{\prime }\approx Dx,y^{\prime }\approx Dy$之上的，后面两个式子是因为$x=\frac{x^{\prime }-W_K}{D}-1,也就是x^{\prime }=Dx+D+W_K,当x>>1时，x^{\prime }\approx Dx$，$bxy=u\approx Rz$则总的访存可以化简为：
$$\begin{gathered} Q_{read}=\frac{2B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_1}{\sqrt{Ruz}}+B{W}_O{H}_O{C}_O \\ =\frac{B{W}_O{H}_O{C}_O{W}_K{H}_K{C}_1}{\sqrt{Ruz}}(2+\frac{\sqrt{Ruz}}{W_K{H}_K{C}_1}) \end{gathered}$$

上式中，括号内的2代表的是读DRAM的比重，后面一个式子代表写DRAM的比重。观察上式可以发现，要是$Q_{DRAM}$最小，则需要$uz$最大，则此时$uz\approx S$，也即表示输出占片内存储主要部分，或者说最小化读的量，
以及$\frac{W_K{H}_K{C}_1}{\sqrt{RS}}>>1$,也即表示写比重可以忽略。
那么，这个式子将满足上面得到的定理二，也就是逼近通信下界。
上面两个约束给出了设计建议：
$\ast 为了达到最小的片外访存，片内存储需要尽可能多地分配给Psum.$
其更详细的要求即上面提到的两条分块参数选取原则：

1. $bxy\approx Rz$，即从两个矩阵当中读入的量相等；
2. $bxyz\approx S即(uz\approx S)且k=1$，即要把几乎片上所有存储全部分配给输出部分。

其背后的原理可以总结为：
使用最少的输入来产生最多的输出，也就是数据复用最大化。此外，对于一些weight比较少的层，写的数量将不可忽略，因此这时就难以逼近通信下界。

---

个人理解：
上面的这两个假设看上去好像是矛盾的，因为第一个约束要求最小化读的量，也就表示输出占片内存储主要部分；而后面的约束要求写的比重足够小。
实际上，如果考虑极端情况，也就是$bxyz=B{W}_O{H}_O{C}_O$时，读次数就是一整张输入图读取一次，并且需要的条件是S足够大，此时不需要分块，无论是读还是写都满足最小次数，无疑是最优解。
但是现实是因为受到$S$大小的限制，必须进行分块。所以本文中片内存储不够的问题就转变成对输出图进行分块的问题。对于写DRAM而言，分块实际上是没有影响的，因为OutR是完全利用的，写次数固定。而分块带来的额外开销主要体现输入和weight的读取上，要遍历所有输出块避免不了输入和weight的重复读取，因此读的比重会因为分块（S的大小）而改变，如果说满足$\frac{W_K{H}_K{C}_1}{\sqrt{RS}}>>1$，则表示输入数据很多，需要分多次读入才能计算完毕，所以在S的固定限制下，输入越多，读DRAM占的比重就越大，当达到一定程度，可以忽略写的比重，也就约接近通信下界。

---

4.2 最小化片上通信的工作负载和存储映射

下面论文开始优化片上部分的通信，也就是GBuf和Reg之间的通信。首先前面已经将input和weight都输入到片内的GBuf中了，现在考虑将伪代码中最内层的循环映射到$p\times q$个PE单元上。

4.3 最小化GBuf通信

首先，片外与片内的访存优化有很大不同，当最小化片外访存时，硬件资源是固定的，也就是片内最大存储$S$固定，不同块之间的负载问题是通过按照循环顺序一个块一个块来解决的。
而对于循环内部，由于输出矩阵已经受到了片内存储容量的限制，所以通过设计PE阵列的大小以及Reg的容量可以实现将循环展开并在同一个时间内完成。并且从GBuf中读取需要的数据可以实现只读一次，这无疑是的GBuf可能的通信下界。
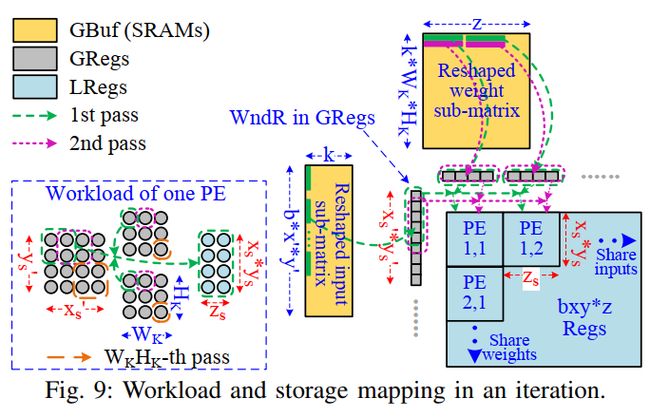
下面具体展开，首先假设PE单元是只包含乘累加单元（MAC)的最小计算单元。下图展示了一个循环中的工作负载示意。

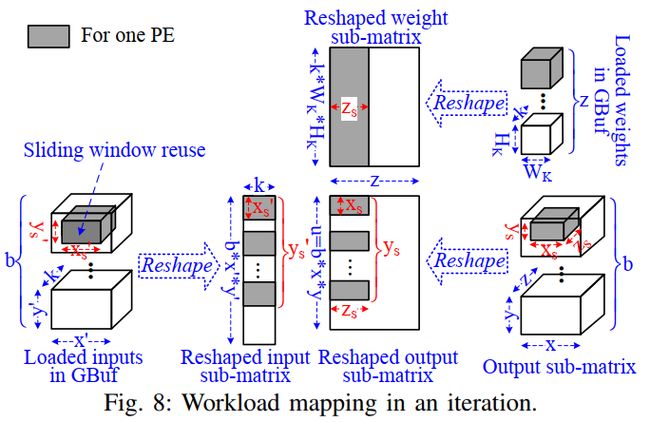
每个PE计算$z_s$输出通道中的$x_s\times y_s$个输出节点，也就是$x_s\times y_s\times z_s$个输出节点。$p\times q$个PE计算的输出节点需要覆盖所有输出节点。下图给了一个工作负载mapping的详细例子：

---

首先考虑单个PE：
对于一个PE，需要$x_s^{\prime }{y}_s^{\prime }k$个输入以及$z_{s}k{W}_K{H}_K$个weight（$k=1$）。不过这些数据不需要一次性读入。为了利用WndR，$x_s^{\prime }\times y_s^{\prime }$个输入被送到Regs中。此外，为了利用InR,从weight Buf中读入$z_s$个weight到Regs中。下面先定义path的概念：

• 一条path是指在一次interation中，同一个时间内更新一次所有的output节点称为一条path。（第i条path就是计算所有输出节点的第i个Psum。

一条path的计算需要$x_s\times y_s\times z_s$个时钟周期。也就是说，每个周期实际上只计算一个乘累加，一个权重要先分别跟$x_s\times y_s$个输入节点的求乘积，一次总共有$z_s$个权重，所以单个path的周期数就是$x_s\times y_s\times z_s$。此外，对于卷积操作而言，每个path计算完的都只是所有卷积操作中的一次乘累加，所以要计算完整的结果需要读入$W_K\times H_K$次weight，并且累加更新$W_K\times H_K$次才得到最后的结果。因此每个input实际上可以用于计算$W_K\times H_K$条path的计算。当然这些值的前提都是$k=1,D=1$。如果考虑k，则所有PE都需要$k{W}_K{H}_K$条path。

下面考虑多个PE:

在同一行的PE共享输入值，而同一列PE共享权重。对于GBuf中的权重都只需要读一次，因此肯定是最小的访存次数。对于输入数据而言，GBuf中的输入平均读取次数为$\frac{x_s^{\prime }{y}_s^{\prime }}{x_s{y}_s}$。是一个大于1的数，这些额外的读取次数是由于卷积的光晕特性（不知道是不是这么翻译），就是说相邻的两个输入block之间要有一定的重合才能使得计算结果是完整的。
文中也提到了可以通过一些复杂的数据传输方式来实现输入数据只要导入一次，但是为了简化设计不考虑这一点。
另外，存储input和weight的Reg可以采用global Regs，例如每行PE都可以复用一个LRegs。实际中，为了避免过高的扇出和长的连线延时，作者将PE阵列划分为若干个groups，每个group共享一组GRegs，且只需要少量的GReg之间的通信作为代价。

关于Psum存在哪里：
本文作者选择将Psum存在LRegs中而不是GBuf中，虽然存在GBuf中可以减少Reg的容量，但是每次path计算完Psum都需要存到GBuf中，之后还要从GBuf中读出来然后更新，会有很多数据交换的操作。而把Psum存在LRegs中则可以避免这一问题，且最小化了GBuf和Reg之间的访存。

关于GBuf容量以及读数据的方式：
此外，通过上述的负载和存储的映射方式，我们会发现，GBuf的容量可得到减少，每次并不需要导入$W_K{H}_{K}zk$个weight和$b{x}^{\prime }{y}^{\prime }k$个input。从等效的矩阵角度，也就是之前的图9所示，对于输入来讲每次只需要导入一列的数据$b{x}^{\prime }{y}^{\prime }$，相当于k=1。同样，对于weight而言，每次只需要读$W_K{H}_{K}z$个数据，也就是图中的一行数据。当做完当前这个pass时，GBuf需要在这之前把数据从DRAM中预取出来，这样就可以实现读数据和运算的pipline。

最小化Reg通信：

Psum存储在LRegs中，每个MAC操作都需要一个Reg写，因此Reg写的最小次数就是MAC操作次数：
$$Q_{reg}=\#ofMACs$$
上式就是Reg的通信下界。将Psum存储在LReg中就能达到这个下界。
假设有$r(\ge x_s{y}_s{z}_s)$个LReg来存储Psum，对于一个PE，在每个周期，最多只会有一个Reg被写入，另外的$r-1$个Reg都处于闲置状态而消耗静态功耗。如果$r$比较大，那么静态功耗将占主导。通过增加PE阵列的尺寸可以可以减小$r$，因为PE数量多了以后每个PE处理的数据就少了。但是计算功耗将上升。不过PE数量变多以后计算速度实际上变快了，所以总的计算能耗实际上不会改变。总之，增加PE将减少Reg的静态功耗，虽然代价是计算功耗会有所上升。

使用GRegs来存储input和weight并被PE阵列共享的方式避免了PE之间的通信。将输入和权重从GBuf复制到GReg带来很少的额外Reg访存。因此Reg之间的通信被最小化了。

5. 通信优化的CNN加速器架构

下面介绍论文提出的CNN加速器架构。首先之前的推导指明了设计方向：为Psum开辟尽可能多的内存，这边考虑有64KB的Psum和大小为$p\times q=16\times 16$的PE阵列。采用16bit的定点运算单元，因此有32K个乘积项，每个PE需要计算128个乘积项。
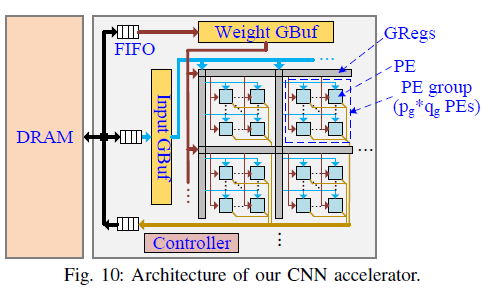
具体的架构图如下所示：

5.1 GBuf

上面也提到了，为了避免长的连续，PE阵列被分为若干个组，每个组包含 $p_g\times q_{g}PEs$ ，每个组共用一个GReg。并且这些GReg行中相同的位置同时被写入数据。
下面讨论如何决定GBuf的大小：
首先，之前的设计准则要求片上存储最好全部用来存Psum（也就是$S\approx 32768$)并且分块参数$\{b,z,y,x\}$需要满足$bxy\approx Rz$,当$R=1$时，$bxy\approx z\approx 181$，这就是$z$的最大近似值。因此存储weight的WGBuf需要开到256的大小（0.5KB）。
对于大的$R$，$bxy$也会变大（因为$bxy\approx Rz$），所以对于较大的R一般可以设置为9（对于3*3的卷积核以及1的步长），由此得到$bxy$的最大值为543.考虑到卷积光晕效应，需要存储的输入实际上为$b{x}^{\prime }{y}^{\prime }$比543会大，因此对于存输入的IGBuf开1024大小，也就是2KB.
可见，上面的IGBuf和WGBuf实际上是比较小的，并且主要用来预取数据。
此外，IGBUF与WGBuf存的数据是按照转换为矩阵的顺序存放的，并且他们再DRAM中也是按照图8的顺序存储的，这也是数据再DRAM中的原始存储方式。也便于后面实现WndR。

5.2 GReg

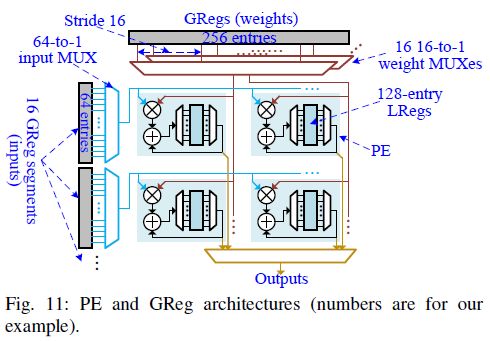
一行GReg被$p_g$个PE行也就是$p_g\times q$P(4*16)个PE共享。GReg行中的数据是从GBuf中拷贝来的为了适应不同的$z$大小，使用一种MUX的结构，如下图所示：

这里有$q$个$\frac{256}{q}-to-1$weight MUXes，连接到WGBuf和$q$(16)个PE列上。跟之前的工作覆盖映射方式有所不同的是，每个PE计算的$z_s$个channel并不是连续的，而是有一个间隔$q$(16)。因为第一次PE计算某一列，而输出图比较大的时候，一次映射不完整个，这样到下一次映射的时候这个PE实际上计算的是$q+1$列。 为了适应不同的$z$以及$z_s$，我们只需要控制weight MUX的选择信号即可。比如，如果$z=64\ (z_s=4)$，则所有的MUX的选择信号就只有0到3，这样就能选择256大小的WGBuf中的前64个元素，而不需要使用复杂的片上网络NoC。 为了实现WndR，每个IGReg被分为$p$(16)段。每段有64个存储并且被$1\times q_g \ (1\times 4)$个PE共享。每个GReg段导入$x_s'y_s'$个输入。他们可以被$W_KH_K$个pass重用来完成$x_sy_sz_s$个输出psum。每个GReg段有一个64到1的MUX来给PE提供数据。选择信号的范围从$0->x_s'y_s'-1$来保证只有前$x_s'y_s'$个输入能被选中。

5.3 PEs

pe内部含有一个MAC单元以及一系列用来存储psum的LReg(128单元)。该架构不需要使用LReg来存储输入和权重。每一周期PE计算一个Psum并将累加结果写入LReg，所有PE都是并行运行。这表示再每个周期实际上MUX的选择信号都是一样的。并且LReg的读写位置也都是一样的。

5.4 Controller

该架构有一个全局控制器，用来调度计算任务。采用状态机来生成各个组件的控制信号，包括读写信号、地址信号以及MUX的选择信号。在PE内部不需要额外的控制器。

6. 实验结果

下面是一些技术细节：

• rtl: verilog
• 综合：DC
• 工艺：65nm
• GBuf：Memory Compiler
• 功耗分析：PTPX
• DDR功耗和延时：CACTI
• DDR属性：DDR3,2GB,峰值带宽6.4GB/s
• Core主频：500MHz
• DDR频率：100MHz
• 对标架构：Eyeriss
• 工作负载：VGG-16, batch size=3

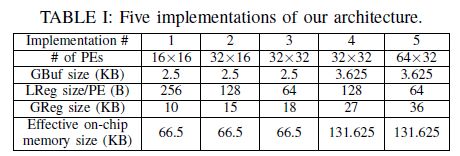
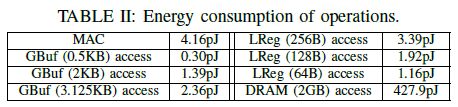
总共评估了五种不同PE阵列大小和片上存储的实现方式，如下表所示。

此外，还评估了每种访存和计算的单位功耗：

6.1 DRAM访存量对比

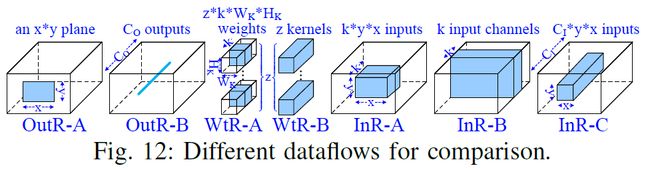
首先，对比了该数据流与其他种类的数据流的性能，下图列举了用于对比的数据流细节：

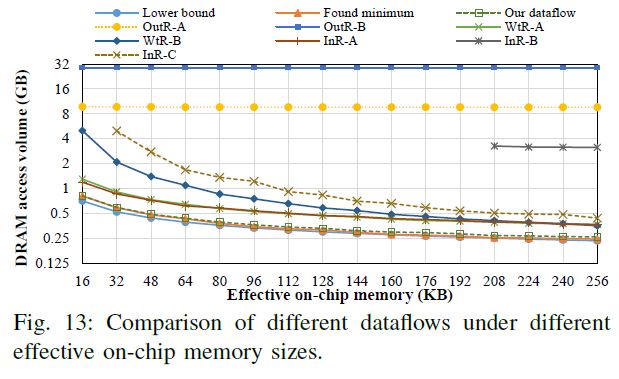
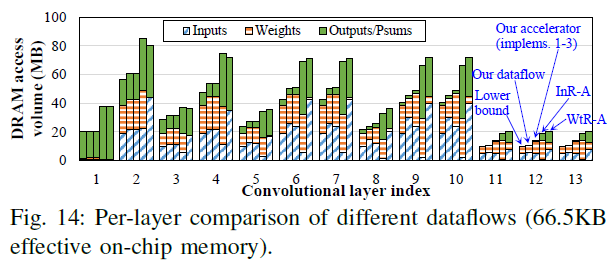
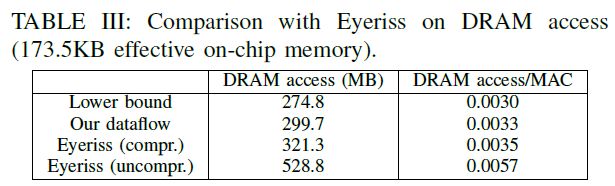
图中，蓝色部分是驻留在片内用于重用的数据。比如对于InR-A而言，一个$kxy$大小的输入块驻留在片上，相应的权重和输出会被反复调取和写入片外。这些数据流覆盖了很多常用的数据流，比如ShiDianNao使用了OutR-A. 下图是不同片上存储容量下各种数据流的片外访存量的对比。为了对比公正，所有数据流的分块参数都是穷举搜索的，因为实际上数据流确定了循环顺序，顺序确定以后搜索最优的分块参数是比较快的。橙色线表示的在每层执行时搜索到的最优数据流的表现，最优数据流是从上面几种中搜索得到的。

从图中可以发现，本文的数据流跟found minimum所差无几，对于所有层只相差4.5%左右的片外访存。之所以本文的数据流无法对所有层都达到最小的访存量，在第三章里已经说明了，该种数据流的访存下界是一个极限近似值，只有当卷积规模够大时才能达到理论最优。 当然，相比之下还是本数据流要优秀，因为found minimum需要搜索多个候选，却只降低了5%的综合片外访存。此外，本文的数据流比理论下界只高出10%左右，远优于InR-A and WtR-A。 下图展示了每层的DRAM访存量，对比的是访存下界，本数据流，本数据流的实际实现，以及INR-A和WtR-B.其中，数据流和其实现存在一定的差距，原因是对片上存储做了一个固定的划分，也就是硬件中固定将64KB划分给Psum，2.5KB划分给GBufs，而对于数据流来说这个划分是可变的。对于另外两种数据流，输出涉及DRAM访问的很大一部分，并且输入和权重访问不平衡，导致更大的内存访问。

下面罗列出了本文跟Eyeriss的访存对比。首先Eyeriss由108KB的GBuf,但是实际上有效的片内存储量为173.5KB，其中100KB是GBuf,8KB用来预取权重，剩下的存储分布在PE内部，每个PE都有448B的内部存储。下图对比了本加速器与经过压缩编码（Run length encode)和未经过压缩编码的Eyeriss的访存对比。

图中可以发现，即使是经过压缩编码的Eyeriss，绝大多数层的访存也比本加速器高出很多。而对于前几层，Eyeriss的表现甚至能优于通信下界，这点在第三章也讨论过了，因为下界的值只是一个极限逼近值，轻负载的时候确实可能会出现比下界值更低的情况。下表从整体上对比了两者的差距。

即使是跟FlexFLow对比（多个数据流选最优的一种加速器），在本文的这种加速器在片外访存量上也比他好33%。

6.2 GReg访存量对比

下图对比了本加速器与Eyeriss在片内访存量上的差距。可以看到对于不同的配置，基本都是完虐Eyeriss.因为不需要GBuf跟内部LReg进行通信。

下表给出了Impl1的各部分访存量，可见对于weight，片外跟片内的读写次数是一样的，也就是所有数只读了一次，无疑是片内访存的通信下界。对于输入而言GBuf的写入次数略多于DRAM读次数，是因为分块操作中，对于输出块的边缘一圈的计算需要用到输入块之外的额外的一圈数据，这导致了写次数的上升。而GBuf的读取次数的上升则是因为WndR。

6.3 Reg访存量

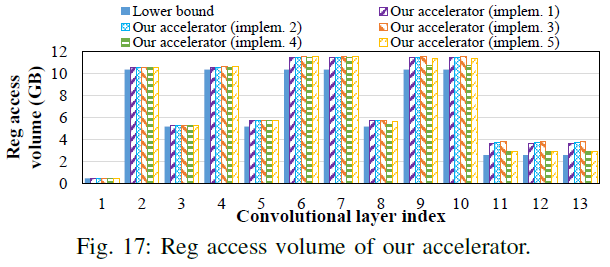
下图比较了本加速器的不同实现在Reg访存上跟理论最优的差距，理论最优的Reg访存就是MAC数量，其中有稍许差距是因为有些Psum会落在输出边界之外，也是由于分块操作引起的。

虽然这个无法跟Eyeriss进行数值上的对比，但应该也是优于Eyeriss的，因为Eueriss需要每次都把Psum写到内部Reg中，并且还要再PE之间传播。

6.4 能效和性能对比

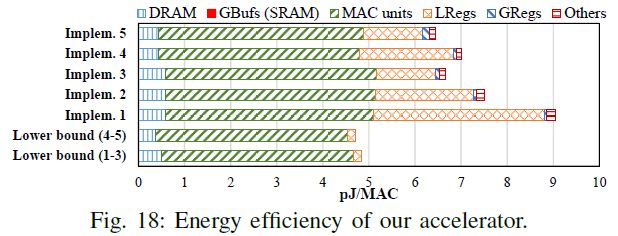
下图对比了本加速器和理论下界的能效对比。可以发现，计算功耗和Reg功耗占主导，片外访存的功耗几乎逼近理论下界。Reg的功耗差距比较大是因为静态功耗，LReg越少，静态功耗越小。
计算功耗占主导是一个很令人振奋的事情！因为这说明该论文的加速器取得了神经网络加速器很大的一个突破，就是打破了访存主导的模式。这样后续就可以针对计算进行优化，而这个部分可以优化的点太多了，近似，稀疏编码，量化等等。

该加速器相对于压缩编码的Eyeriss，在能耗可以取得2.61-3.68倍的提升（eyeriss 22.1pJ/MAC），不过这个数值是仿真数值，流片出来可能会有所减少。
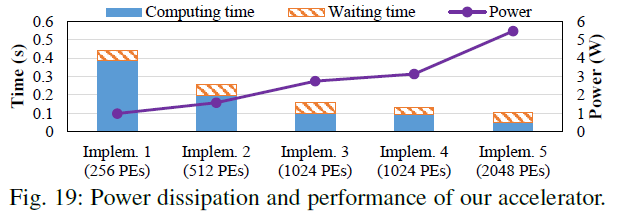
下图是性能和能耗的数值图。pe规模越大，能耗越高，性能越高，等待时间也越长。从性能上，相比Eyeriss,这五种impl达到了9.8-42.3倍的性能提升，并考虑了存储访问延时。

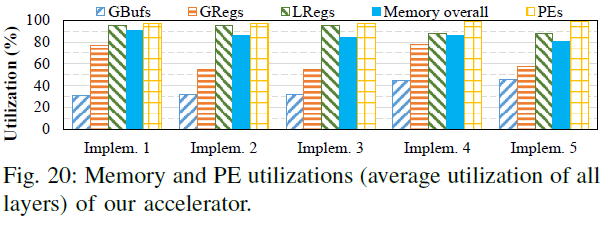
6.5 存储和PE利用率

最后一张图展示了存储和PE利用率：

其中，GBuf和GReg利用率低是因为有冗余的SRAM和GReg用来适配不同的分块参数。LReg的利用率非常高。增加PE数量会降低LReg利用率，因为减轻了PE的负载。此外，整个PE阵列的利用率也非常高。

写在最后：
不得不佩服陈晓明老师团队的算法和数学功底，个人感觉本文最主要的精髓就是卷积下界的推导，找到了一种能够刻画神经网络加速器片内片外通信的模型（红蓝卵石），从理论角度给出了加速器设计中的设计原则，非常具有说服力。坐等陈老师团队后续给出流片实测的结果。

引用：
Chen X , Han Y , Wang Y . Communication Lower Bound in Convolution Accelerators[J]. 2019.