DPCM差分预测编码原理及实现

DPCM差分预测编码

算法原理

DPCM编解码的框图如下所示，可以很明显得发现这是一个带有负反馈的算法系统。

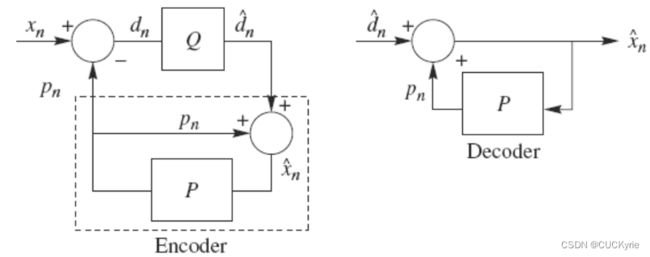
如上图所示，首先输入一个像素值，与上一个像素的预测值做差，将得到的差值进行编码，编码后的差值有两个去向：一个是直接输出，另一个是通过解码器反解出差值，和上一像素的预测值相加，就得到了当前像素的预测值，为下一个像素的到来做准备。

实现功能

本次采用左侧预测，并且默认最左侧像素前的真实值为均为128。并且实现了如下功能：

• 进行不同量化bit数的差分预测编码
• 将编码结果进行输出并进行霍夫曼编码
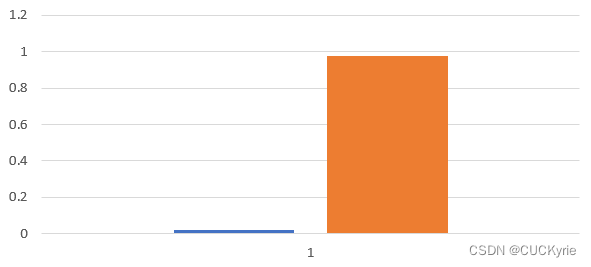
• 分别计算原图像和量化后的图像进行概率分布
• 分别计算原图像经过熵编码和经过DPCM+熵编码的图像的压缩比
• 比较二者压缩效率
• 计算重建图像的PSNR

实验代码

#include 
#include 
#include 
#include 
#include 
#define uchar unsigned char
#define ll long long

using namespace std;

const string path = "C:\\Users\\sdlwq\\Desktop\\test\\Lena256B.yuv"; // 原始图像4:1:1
const string build_out = "build.yuv"; // 重建
const string code_out = "code.yuv"; // 量化编码
const int width = 256;
const int height = 256;
double freq[256];

uchar* input_buffer; //原始图像
uchar* out_buffer;  //重建图
uchar* code_buffer;  //量化输出
uchar* u_buffer;  // 色差信号
uchar* v_buffer;
int bitnum;

inline void calculate_freq(uchar* buffer) //计算概率分布
{
    memset(freq, 0.0, sizeof(freq));
    for (int i = 0;i < height * width;i ++) freq[buffer[i]] += 1.0;
    for (double & i : freq) i /= (height * width);
}

inline int limit(int val, int low, int high)
{
    if (val < low) return low;
    else if (val > high) return high;
    else return val;
}

inline double PSNR(uchar* standard, uchar* image)
{
    int max = 255;
    double mse = 0;
    for (int i = 0; i < height; i ++) {
        for (int j = 0; j < width; j ++) {
            mse += (standard[i * width + j] - image[i * width + j]) * (standard[i * width + j] - image[i * width + j]);
        }
    }
    mse = (double)mse / (double)(width * height);
    double psnr = 10 * log10((double)(max * max) / mse);
    cout << "PSNR = " << psnr;
}

int main()
{
    int length = width * height;
    ifstream in(path, ios :: binary);
    if (!in.is_open()) {
        cout << "Open failed" << endl;
        exit(-1);
    }
    else cout << "Open Successfully" << endl;
    input_buffer = new uchar[length];
    out_buffer = new uchar[length];
    code_buffer = new uchar[length];
    u_buffer = new uchar[length / 2];
    v_buffer = new uchar[length / 2];
    in.read((char*)input_buffer, length);
    // 计算一下原始的像素值分布
    ofstream out;
    out.open( "original.csv", ios :: out);
    calculate_freq(input_buffer);
    if (!out.is_open()) {
        cout << "CSV Open Failed" << endl;
        exit(-1);
    }
    for (int i = 0;i < 256;i ++) out << i << ',' << freq[i] << endl;
    out.close();
    cout << "Write Successfully" << endl;
    memset(u_buffer, 128, length / 2);
    memset(v_buffer, 128, length / 2);
    // 分别进行8bit，4bit，2bit和1bit量化
    int prediction, preError, enqPreError;
    for (auto i : {8, 4, 2, 1}) {
        for (int h = 0;h < height;h ++) {
            prediction = 128;
            preError = input_buffer[h * width] - prediction;
            int temp = (preError + 128) / pow(2, 8 - i);
            code_buffer[h * width] = limit(temp, 0, pow(2, i) - 1);
            enqPreError = code_buffer[h * width] * pow(2, 8 - i) - 128;
            out_buffer[h * width] = limit(enqPreError + prediction, 0, 255);
            for (int w = 1;w < width;w ++) {
                prediction = out_buffer[h * width + w - 1];
                preError = input_buffer[h * width + w] - prediction;
                int temp = (preError + 255) / pow(2, 9 - i);
                code_buffer[h * width + w] = limit(temp, 0, (pow(2, i) - 1));
                enqPreError = code_buffer[h * width + w] * pow(2, 9 - i) - 255;
                out_buffer[h * width + w] = limit(enqPreError + prediction, 0, 255);
            }
        }

        cout << "Translate Successfully" << endl;
        string str;
        str += ('0' + i);
        str += "bit";
        cout << str << endl;

        out.open(str + build_out, ios :: binary);
        out.write((char*)out_buffer, length);
        out.write((char*)u_buffer, length / 2);
        out.write((char*)v_buffer, length / 2);
        out.close();

        out.open(str + code_out, ios :: binary);
        out.write((char*)code_buffer, length);
        out.write((char*)u_buffer, length / 2);
        out.write((char*)v_buffer, length / 2);
        out.close();

        double residualFre[255] = {0};
        calculate_freq(code_buffer);
        out.open(str + "code.csv", ios::out);
        for( int k = 0; k < (1 << i); k ++) out << k << "," << freq[k] << endl;
        cout << i << "bit psnr: "<< PSNR( input_buffer, out_buffer) << endl;

        delete[] input_buffer;
        delete[] code_buffer;
        delete[] out_buffer;
        delete[] u_buffer;
        delete[] v_buffer;
        cout << i << "bit complete" << endl;
    }
    return 0;
}

实验过程

通过运行上面的代码，我们可以得到8，4，2，1bit下的重建图像和量化误差图像。同时得到了每种bit量化下的编码概率分布及其PSNR值，下面我们来分别对原图和量化后的编码进行熵编码，本次实验采用Huffman编码。

使用以下bat指令：

huff_run.exe -i 8bitcode.yuv -o 8bitcode.huff -c -t 8bitcode.txt
huff_run.exe -i 4bitcode.yuv -o 4bitcode.huff -c -t 4bitcode.txt
huff_run.exe -i 2bitcode.yuv -o 2bitcode.huff -c -t 2bitcode.txt
huff_run.exe -i 1bitcode.yuv -o 1bitcode.huff -c -t 1bitcode.txt
huff_run.exe -i Lena256B.yuv -o standard.huff -c -t standard.txt

即可得到经过熵编码后的数据。

实验结果

注意：这里我们压缩比按照$\frac{Afte{r}_{Huff}}{Original}$来计算。

	8 bit	4 bit	2 bit	1 bit
量化误差图
重建图像
概率分布图
压缩比	51.055%	29.075%	25.709%	25.017%
PSNR	51.147	23.139	11.935	9.956

如果将原始图像直接进行熵编码，压缩比为71.09%。

可见经过熵编码之后，图像的大小会减小。
经过DCMP+熵编码之后，图像大小比直接使用熵编码减小的更多，随着量化比特数的减小，压缩效率越来越高，但是变化越来越缓慢；于此同时，图像质量，也就是PSNR的值迅速恶化，重建出的图像质量越来越差，到1bit是就已经很模糊了。
综上，量化应采用合适的量化比特数，使之既不至于太影响画面，又可以达到较高的压缩效率。