【MATLAB】无人驾驶车辆的模型预测控制技术(精简讲解和代码)【运动学轨迹规划】
文章目录
- 0.友情链接
- 1.引言
- 2.预测模型
- 3.滚动优化
-
- 3.1.线性化
- 3.2. U r U_r Ur的求取
- 3.3.离散化与序列化
- 3.4.实现增量控制
- 4.仿真示例
0.友情链接
- B站链接1-北京理工大学无人驾驶技术课程
- B站链接2-MATLAB实现模型预测控制
- B站链接3-北京理工大学的学生讲解无人驾驶车辆的模型预测控制
- B站链接4-英国谢菲尔德大学模型预测控制网课(全英文)
- IEEE论文参考:Model Predictive Control for Visual Servo Steering of Nonholonomic Mobile Robots(非完整移动机器人视觉伺服转向的模型预测控制)
- 书籍参考:国之重器出版社《无人驾驶车辆模型预测控制(第二版)》
- 书籍配套代码下载链接
- 本文完整配套代码链接
- 阿克曼转向原理介绍
1.引言
\qquad MATLAB自身是带预测控制模块的,但是看了一些MATLAB的预测模块使用教程视频,仍然不如自己书写代码原理清晰,而且MATLAB的预测控制是基于状态方程的滑模控制,并不包含所有预测控制的种类,使用范围有限。因此我想按照预测控制的原理,逐步为大家讲解预测控制算法及MATLAB代码的书写步骤。
\qquad Simulink自身也携带一个关于无人驾驶的模块Car_sim,但是Car_sim使用的模型比一般的模型更复杂,因此本人参考《无人驾驶车辆的模型预测控制》中的
\qquad 预测控制都包含三个主要步骤——预测模型、滚动优化和反馈矫正。按照模型的不同,可以分为动态矩阵算法、广义极点配置、基于状态方程的滑模控制。现代控制理论中,以状态方程为主要模型,本文也以其为例建立模型,其他的模型原理与其类似,只是求解方法有所差异。
\qquad 为了方便大家理解,本人不直接列出所有代码,而是按照讲解和代码对照的方式,逐步展现每个环节的代码,最终展现全部代码和效果。那我们就从第一步开始吧。
2.预测模型
\qquad 建立预测模型的目的在于获取输入量(控制量)和输出量(以及其他干扰项)的映射关系。在本例(汽车变道)示例中,控制量是前轮角度 ϕ \phi ϕ和汽车速度大小 v v v,而输出量则是汽车的质心与待变道直线的距离。控制的目的是让汽车的质心尽快接近待变道直线,并维持其在该直线上运动。
\qquad 我们的思路已经很清晰了,但是别着急,我们似乎忽略了什么。例如汽车的速度不能是无穷大,前轮的角度也是有限制的。我们取车辆的后轴中心速度大小限制为 [ v m i n , v m a x ] [v_{min},v_{max}] [vmin,vmax],前轮角度绝对值限幅为 ϕ m \phi_m ϕm。前轮转动的这个角度,又称为车辆的横摆角。变道的情况如下图所示:
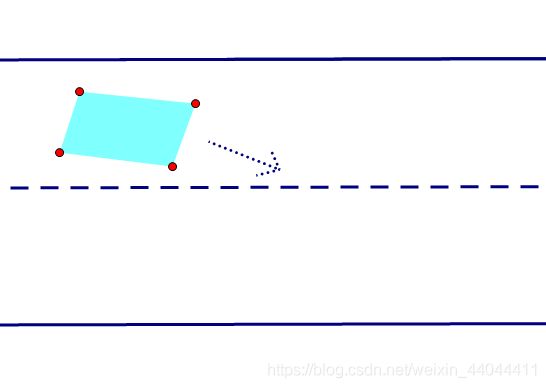
\qquad 汽车是前轮驱动还是后轮驱动直接决定了控制量是前轮的速度还是后轮速度,当然前后轮速度是可以通过后轴中心速度和车辆横摆角转换得到的。因此设小汽车后轴速度为 v d v_d vd,车辆横摆角为 ϕ \phi ϕ,同时设车长为 l l l。以上图左下角为原点建立坐标系。(不知道阿克曼转向原理的可以看一下友情链接的介绍,这里用的是简化的两轮模型)
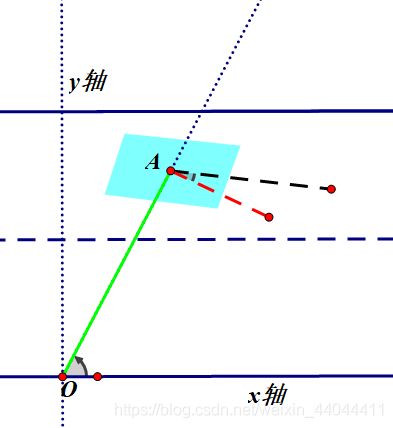
\qquad 黑色虚线代表了汽车朝向,而红色虚线则是前轮的朝向。二者夹角为横摆角 ϕ \phi ϕ,以逆时针为正方向。汽车可以看成是二维平面的刚体,因此只需要三个参数就可以确定其状态。我们选取它质心的横纵坐标 x , y x,y x,y加汽车朝向与x轴逆时针方向的夹角 θ \theta θ作为状态变量。(在一篇IEEE的文章上看到选取极坐标作为状态变量的方法,也是可行的,但对于变道这种单移线运动来说,直角坐标更加方便)。采用 S S S表示状态向量, U U U表示控制向量。
\qquad 汽车的后轮速度大小 v d v_d vd和汽车的朝向 θ \theta θ决定了一小段时间内汽车的位移 ( δ x , δ y ) (\delta x,\delta y) (δx,δy),而前轮的转向角 ϕ \phi ϕ则决定了一小段时间汽车朝向的变化量 δ θ \delta \theta δθ。状态方程列写如下:
S ′ = [ x ′ y ′ θ ′ ] = [ v d c o s θ v d s i n θ v d t a n ϕ / l ] = f ( S , U ) S'= \begin{bmatrix} x' \\[1ex] y' \\[1ex] \theta'\\[1ex] \end{bmatrix} = \begin{bmatrix} v_d cos\theta \\ v_d sin \theta \\ v_d tan\phi/l \end{bmatrix}= f(S,U) S′=⎣⎢⎢⎡x′y′θ′⎦⎥⎥⎤=⎣⎡vdcosθvdsinθvdtanϕ/l⎦⎤=f(S,U)
\qquad 模拟阿克曼转向的车辆的MATLAB代码如下:
function [X,Y,Th] = car_run(X,Y,Th,L,dt,vd,phi)
X = X + vd*cos(Th)*dt;
Y = Y + vd*sin(Th)*dt;
Th = Th + vd*tan(phi)/L*dt;
end
X和Y为车辆后轴中心的位置信息,Th为车辆的朝向,L为车长,dt为仿真采样间隔,vd为车辆后轴速度,phi为车辆横摆角。
3.滚动优化
3.1.线性化
\qquad 滚动优化的目的是根据预测模型和控制目的,建立目标函数和约束条件,并在约束条件内,求得目标函数的最优解(即期望控制量),从而达到预测控制的目的。
\qquad 求目标函数极小值的方法有很多,智能优化算法依赖于蒙特卡洛模拟,数值优化算法依赖于函数的导数。前者比后者的实用性更大,但是速度更慢。汽车行驶中的在线规划对运算速度的要求高,因此普遍采用后者进行求函数极小值的操作。
\qquad 二次规划是数值优化算法中一类特殊的优化问题,即特指目标函数为二次型 1 2 x T H x + c T x \frac{1}{2}x^THx+c^Tx 21xTHx+cTx,约束条件为线性约束的(线性不等式约束+线性灯等式约束)的有约束优化问题。将预测模型的目标函数转换为二次规划问题的模型预测控制(MPC)又称为线性预测控制(LPC),其运算速度是MPC中最快的。本文将以无人驾驶领域为例,介绍模型的线性化过程。
\qquad 汽车在变道时,给定期望的轨迹 ( x r , y r ) (x_r,y_r) (xr,yr),并通过控制变量使汽车在时域上经过的路径逼近期望轨迹。当然,我们期望汽车的朝向 θ \theta θ最终逼近于0(即直线行驶),期望的状态量使用 S r S_r Sr表示,则我们的目的是使 ∣ S − S r ∣ |S-S_r| ∣S−Sr∣即 ( S − S r ) 2 / 2 (S-S_r)^2/2 (S−Sr)2/2最小。当期望状态向量与实际状态向量相差较小且期望控制量与实际控制量相差较小时,可采用在 S r S_r Sr处的导数 d y / d x dy/dx dy/dx来代替变化率 Δ y / Δ x \Delta y/ \Delta x Δy/Δx:
S ′ − S r ′ = f ( S , U ) − f ( S r , U r ) ≈ ∂ f ∂ S ∣ S r ⋅ ( S − S r ) + ∂ f ∂ U ∣ U r ⋅ ( U − U r ) = A ⋅ ( S − S r ) + B ⋅ ( U − U r ) \begin{array}{l} S'-S'_r=f(S,U)-f(S_r,U_r)\\[2ex] ≈\frac {\partial f}{\partial S}|_{S_r}\cdot(S-S_r)+\frac {\partial f}{\partial U}|_{U_r}\cdot(U-U_r)\\[2ex] =A\cdot(S-S_r)+B\cdot(U-U_r) \end{array} S′−Sr′=f(S,U)−f(Sr,Ur)≈∂S∂f∣Sr⋅(S−Sr)+∂U∂f∣Ur⋅(U−Ur)=A⋅(S−Sr)+B⋅(U−Ur)
其中
A = ∂ f ∂ S ∣ S r = [ ∂ f 1 ∂ S 1 ∂ f 1 ∂ S 2 ∂ f 1 ∂ S 3 ∂ f 2 ∂ S 1 ∂ f 2 ∂ S 2 ∂ f 2 ∂ S 3 ∂ f 3 ∂ S 1 ∂ f 3 ∂ S 2 ∂ f 3 ∂ S 3 ] = [ 1 0 − v d r ∗ s i n ( θ r ) 0 1 v d r ∗ c o s ( θ r ) 0 0 1 ] B = ∂ f ∂ U ∣ U r = [ ∂ f 1 ∂ U 1 ∂ f 1 ∂ U 2 ∂ f 2 ∂ U 1 ∂ f 2 ∂ U 2 ∂ f 3 ∂ U 1 ∂ f 3 ∂ U 2 ] = [ c o s ( θ r ) 0 s i n ( θ r ) 0 t a n ( ϕ r ) / l v d r ∗ s e c 2 ( ϕ r ) / l ] A=\frac {\partial f}{\partial S}|_{S_r}= \begin{bmatrix} \frac{\partial f_1}{\partial S_1} & \frac{\partial f_1}{\partial S_2} & \frac{\partial f_1}{\partial S_3}\\[2ex] \frac{\partial f_2}{\partial S_1} & \frac{\partial f_2}{\partial S_2} & \frac{\partial f_2}{\partial S_3}\\[2ex] \frac{\partial f_3}{\partial S_1} & \frac{\partial f_3}{\partial S_2} & \frac{\partial f_3}{\partial S_3}\\[2ex] \end{bmatrix}= \begin{bmatrix} 1 & 0 & -v_{dr}*sin(\theta_r) \\ 0 & 1 & v_{dr}*cos(\theta_r)\\ 0 & 0 & 1\\ \end{bmatrix} \\ B=\frac {\partial f}{\partial U}|_{U_r}= \begin{bmatrix} \frac{\partial f_1}{\partial U_1} & \frac{\partial f_1}{\partial U_2}\\[2ex] \frac{\partial f_2}{\partial U_1} & \frac{\partial f_2}{\partial U_2}\\[2ex] \frac{\partial f_3}{\partial U_1} & \frac{\partial f_3}{\partial U_2}\\[2ex] \end{bmatrix}= \begin{bmatrix} cos(\theta_r) & 0 \\[1ex] sin(\theta_r) & 0 \\[1ex] tan(\phi_r)/l & v_{dr}*sec^2(\phi_r)/l \\[1ex] \end{bmatrix} A=∂S∂f∣Sr=⎣⎢⎢⎢⎢⎡∂S1∂f1∂S1∂f2∂S1∂f3∂S2∂f1∂S2∂f2∂S2∂f3∂S3∂f1∂S3∂f2∂S3∂f3⎦⎥⎥⎥⎥⎤=⎣⎡100010−vdr∗sin(θr)vdr∗cos(θr)1⎦⎤B=∂U∂f∣Ur=⎣⎢⎢⎢⎢⎡∂U1∂f1∂U1∂f2∂U1∂f3∂U2∂f1∂U2∂f2∂U2∂f3⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎡cos(θr)sin(θr)tan(ϕr)/l00vdr∗sec2(ϕr)/l⎦⎥⎥⎤
记 S ′ ~ = S ′ − S r ′ , S ~ = S − S r , U ~ = U − U r \widetilde{S'}=S'-S'_r,\widetilde{S}=S-S_r,\widetilde{U}=U-U_r S′ =S′−Sr′,S =S−Sr,U =U−Ur
则线性化后的模型为
S ′ ~ = A S ~ + B U ~ \widetilde{S'}=A\widetilde{S}+B\widetilde{U} S′ =AS +BU
即我们所熟知的线性状态方程。我们的目标是使得汽车按照既定的轨迹形式,因此希望实际状态逼近于期望状态,即 ∣ ∣ S ~ ∣ ∣ → 0 ||\widetilde{S}||\rightarrow0 ∣∣S ∣∣→0,因此输出方程即为
Y = S ~ Y=\widetilde{S} Y=S
3.2. U r U_r Ur的求取
\qquad 期望状态向量 S r S_r Sr是容易理解的,无人驾驶车辆需要提前规划形式的路径 ( x r , y r ) (x_r,y_r) (xr,yr),有时还对车辆的朝向有所要求( θ r \theta_r θr),那么期望控制量 U r U_r Ur又是怎么得出的呢?其实很简单,在没有约束条件的情况下,根据状态方程即可得到 U r U_r Ur的取值。根据状态方程我们可以得知:
{ x r ′ = v d r c o s ( θ r ) y r ′ = v d r s i n ( θ r ) θ r ′ = v d r t a n ϕ r / l ⇒ { v d r = ( x r ′ ) 2 + ( y r ′ ) 2 ϕ r = a t a n ( l ⋅ θ r ′ / v d r ) \begin{cases} x'_r=v_{dr}cos(\theta_r)\\ y'_r=v_{dr}sin(\theta_r)\\ \theta'_r=v_{dr}tan\phi_r /l\\ \end{cases} \Rightarrow \begin{cases} v_{dr}=\sqrt{(x'_r)^2+(y'_r)^2}\\ \phi_r=atan(l\cdot \theta'_r/v_{dr}) \end{cases} ⎩⎪⎨⎪⎧xr′=vdrcos(θr)yr′=vdrsin(θr)θr′=vdrtanϕr/l⇒{vdr=(xr′)2+(yr′)2ϕr=atan(l⋅θr′/vdr)
\qquad 在实际系统中,若 S = ( x r , y r , θ r ) S=(x_r,y_r,\theta_r) S=(xr,yr,θr)是离散取值的,可以借助三次样条插值的方法补全需要的值,并用差分替代微分求取状态量的导数。样条差值的方法在此不再赘述,仿真时建议使用MATLAB的pchip函数。
本部分对应的MATLAB代码如下
X_r = [0,1,2,3,4,5,6]*3; % X的期望坐标
Y_r = [3,3,2,1,0,0,0]; % Y的期望坐标
L=2.5; % 车身长度
v0 = 10; % 期望速度
T = 20e-3; % 控制周期20ms
dt = 1e-3; % 仿真周期1ms
Xr = linspace(X_r(1),X_r(numel(X_r)),(X_r(numel(X_r))-X_r(1))/(T*v0)); % 横坐标期望值的插值序列
Yr = pchip(X_r,Y_r,Xr); % 通过三次样条插值算出纵坐标坐标插值序列
n = numel(Yr); % 预测模型中所有规划点
FYr = Yr(2:n);
dYr = zeros(1,n);
dYr(1:n-1) = FYr - Yr(1:n-1);
dYr(n) = dYr(n-1);%保证导数连续
FXr = Xr(2:n);
dXr = zeros(1,n);
dXr(1:n-1) = FXr - Xr(1:n-1);
dXr(n) = dXr(n-1);
Thr = atan(dYr./dXr); % 车朝向角的期望值
FThr = Thr(2:n);
dThr = zeros(1,n);
dThr(1:n-1) = FThr-Thr(1:n-1);
dThr(n)=dThr(n-1);
vdr = sqrt(dXr.^2+dYr.^2)/T; % 车后轮的期望速度
Phr = atan(L./vdr.*dThr/T); % 车前轮的偏转角
这里以变道为例,绘制期望轨迹 ( X r , Y r ) (X_r,Y_r) (Xr,Yr)如下图
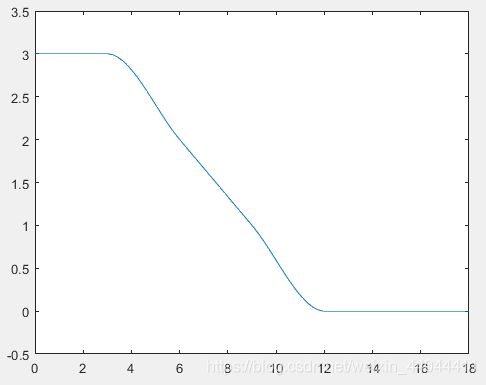
\qquad 可以发现,车辆从上道(y=3)逐步变化至下道(y=0)。样条插值后的轨迹并不是折线,但由于不一定满足车辆的物理约束,因此不能用期望控制量作为实际控制量进行控制。
3.3.离散化与序列化
\qquad 预测控制依赖于计算机,计算机的控制信号是离散的,因此我们还需要把线性化后的状态方程离散化。假设控制周期为 T T T,则离散化后的状态方程为:
S ~ ( k + 1 ) − S ~ ( k ) T = A k S ~ ( k ) + B k U ~ ( k ) ⇒ S ~ ( k + 1 ) = ( A k T + I ) S ~ ( k ) + B k T U ~ ( k ) ⇒ S ~ ( k + 1 ) = A k ∗ S ~ ( k ) + B k ∗ U ~ ( k ) \begin{array}{l} \frac{\widetilde{S}(k+1)-\widetilde{S}(k)}{T}=A_k\widetilde{S}(k)+B_k\widetilde{U}(k) \\[2ex] \Rightarrow \widetilde{S}(k+1)=(A_kT+I)\widetilde{S}(k)+B_kT\widetilde{U}(k) \\ \Rightarrow \widetilde{S}(k+1)=A^*_k\widetilde{S}(k)+B^*_k\widetilde{U}(k)\\ \end{array} TS (k+1)−S (k)=AkS (k)+BkU (k)⇒S (k+1)=(AkT+I)S (k)+BkTU (k)⇒S (k+1)=Ak∗S (k)+Bk∗U (k)
\qquad 接着我们需要选择接下来需要预测的未来若干个采样时刻的状态量的个数和控制量个数,即预测时域 N N N和控制时域 M M M( M ≤ N M≤N M≤N)。我们采取最简单的情形 M = N M=N M=N讲解。
\qquad 首先列写未来 N N N个时刻的离散状态方程
{ S ~ ( k + 1 ) = A k ∗ S ~ ( k ) + B k ∗ U ~ ( k ) S ~ ( k + 2 ) = A k + 1 ∗ S ~ ( k + 1 ) + B k + 1 ∗ U ~ ( k + 1 ) ⋯ S ~ ( k + N ) = A k + N − 1 ∗ S ~ ( k + N − 1 ) + B k + N − 1 ∗ U ~ ( k + N − 1 ) ⇒ S ~ ( k + i ) = A A i S ~ ( k ) + A B 1 U ~ ( k ) + A B 2 U ~ ( k + 1 ) + . . . + A B i U ~ ( k + i − 1 ) \begin{cases} \widetilde{S}(k+1)=A^*_k\widetilde{S}(k)+B^*_k\widetilde{U}(k)\\ \widetilde{S}(k+2)=A^*_{k+1}\widetilde{S}(k+1)+B^*_{k+1}\widetilde{U}(k+1)\\ \qquad \qquad \cdots \\ \widetilde{S}(k+N)=A^*_{k+N-1}\widetilde{S}(k+N-1)+B^*_{k+N-1}\widetilde{U}(k+N-1)\\ \end{cases}\\ \Rightarrow \widetilde{S}(k+i)=AA_i\widetilde{S}(k)+AB_1\widetilde{U}(k)+AB_2\widetilde{U}(k+1)+...+AB_i\widetilde{U}(k+i-1) ⎩⎪⎪⎪⎨⎪⎪⎪⎧S (k+1)=Ak∗S (k)+Bk∗U (k)S (k+2)=Ak+1∗S (k+1)+Bk+1∗U (k+1)⋯S (k+N)=Ak+N−1∗S (k+N−1)+Bk+N−1∗U (k+N−1)⇒S (k+i)=AAiS (k)+AB1U (k)+AB2U (k+1)+...+ABiU (k+i−1)
其中
{ A A i = A k + i − 1 ∗ A k + i − 2 ∗ . . . A k ∗ A B 1 ( i ) = A k + i − 1 ∗ A k + i − 2 ∗ . . . A k + 1 ∗ B k ∗ A B 2 ( i ) = A k + i − 1 ∗ A k + i − 2 ∗ . . . A k + 2 ∗ B k + 1 ∗ ⋯ A B i − 1 ( i ) = A k + i − 1 ∗ B k + i − 2 ∗ A B i ( i ) = B k + i − 1 ∗ \begin{cases} AA_i=A^*_{k+i-1}A^*_{k+i-2}...A^*_{k} \\ AB_1^{(i)}=A^*_{k+i-1}A^*_{k+i-2}...A^*_{k+1}B^*_k \\ AB_2^{(i)}=A^*_{k+i-1}A^*_{k+i-2}...A^*_{k+2}B^*_{k+1} \\ \qquad \cdots \\ AB_{i-1}^{(i)}=A^*_{k+i-1}B^*_{k+i-2} \\ AB_{i}^{(i)}=B^*_{k+i-1} \\ \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧AAi=Ak+i−1∗Ak+i−2∗...Ak∗AB1(i)=Ak+i−1∗Ak+i−2∗...Ak+1∗Bk∗AB2(i)=Ak+i−1∗Ak+i−2∗...Ak+2∗Bk+1∗⋯ABi−1(i)=Ak+i−1∗Bk+i−2∗ABi(i)=Bk+i−1∗
\qquad 已知量为 S ~ ( k ) , A k ∗ , B k ∗ \widetilde{S}(k),A^*_k,B^*_k S (k),Ak∗,Bk∗,后两者是因为期望状态量和期望控制量已知因此也已知,但由于期望状态量是一个时间序列,因此矩阵 A k ∗ , B k ∗ A^*_k,B^*_k Ak∗,Bk∗也是一个时间序列。输入为 U ~ ( k ) , U ~ ( k + 1 ) , . . . , U ~ ( k + N ) \widetilde{U}(k),\widetilde{U}(k+1),...,\widetilde{U}(k+N) U (k),U (k+1),...,U (k+N),输出为 S ~ ( k + 1 ) , S ~ ( k + 2 ) , . . . . , S ~ ( k + N ) \widetilde{S}(k+1), \widetilde{S}(k+2),...., \widetilde{S}(k+N) S (k+1),S (k+2),....,S (k+N),记
S ~ ^ = [ S ~ ( k + 1 ) , S ~ ( k + 2 ) , . . . . , S ~ ( k + N ) ] T U ~ ^ = [ U ~ ( k ) , U ~ ( k + 1 ) , . . . , U ~ ( k + N − 1 ) ] T U ^ = [ U ( k ) , U ( k + 1 ) , . . . , U ( k + N − 1 ) ] T \widehat{ \widetilde{S}}=[\widetilde{S}(k+1), \widetilde{S}(k+2),...., \widetilde{S}(k+N)]^T \\ \widehat{\widetilde{U}}=[\widetilde{U}(k),\widetilde{U}(k+1),...,\widetilde{U}(k+N-1)]^T \\ \widehat{U}=[U(k),U(k+1),...,U(k+N-1)]^T S =[S (k+1),S (k+2),....,S (k+N)]TU =[U (k),U (k+1),...,U (k+N−1)]TU =[U(k),U(k+1),...,U(k+N−1)]T
根据上面的推导,可以推出序列化后的状态方程:
S ~ ^ = A A ⋅ S ~ ( k ) + B B ⋅ U ~ ^ s . t . { v m i n ≤ v d ≤ v m a x − ϕ m ≤ ϕ ≤ ϕ m \widehat{ \widetilde{S}}=AA\cdot \widetilde{S}(k)+BB\cdot\widehat{\widetilde{U}} \\ s.t.\begin{cases} v_{min}≤v_d≤v_{max} \\ -\phi _m ≤\phi≤\phi_m \end{cases} S =AA⋅S (k)+BB⋅U s.t.{vmin≤vd≤vmax−ϕm≤ϕ≤ϕm
其中
A A = [ A A 1 A A 2 ⋮ A A N ] B B = [ A B 1 ( 1 ) 0 ⋯ 0 A B 1 ( 2 ) A B 2 ( 2 ) ⋯ 0 ⋮ ⋮ ⋱ ⋮ A B 1 ( N ) A B 2 ( N ) ⋯ A B N ( N ) ] AA= \begin{bmatrix} AA_1 \\AA_2\\ \vdots \\AA_N \end{bmatrix}\\[2ex] BB = \begin{bmatrix} AB_1^{(1)} & 0 &\cdots & 0 \\ AB_1^{(2)} & AB_2^{(2)} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ AB_1^{(N)} & AB_2^{(N)} &\cdots & AB_{N}^{(N)} \end{bmatrix} AA=⎣⎢⎢⎢⎡AA1AA2⋮AAN⎦⎥⎥⎥⎤BB=⎣⎢⎢⎢⎢⎡AB1(1)AB1(2)⋮AB1(N)0AB2(2)⋮AB2(N)⋯⋯⋱⋯00⋮ABN(N)⎦⎥⎥⎥⎥⎤
优化问题为
U ^ = a r g min U ^ 1 2 S ~ ^ T Q S ~ ^ + 1 2 U ^ T P U ^ \widehat{U}=arg\min_{\widehat{U}}{\frac{1}{2}\widehat{ \widetilde{S}}^TQ\widehat{ \widetilde{S}}+\frac{1}{2}\widehat{U}^TP\widehat{U}} U =argU min21S TQS +21U TPU
3.4.实现增量控制
\qquad 除了保证车辆基本的约束外,为了保证车辆的舒适性,还应防止控制量的突变,即车辆的加速度和打方向盘的速度不至于过快。控制量的加速度不宜过大,需要在约束条件中增加关于控制量变化率的硬约束和在目标函数增加关于控制量变化率的软约束。
\qquad 硬约束很好理解,即对控制增量进行限幅
{ a m i n ≤ v d ′ ≤ a m a x − d ϕ m ≤ ϕ ′ ≤ d ϕ m \begin{cases} a_{min}≤v'_d≤a_{max} \\ -d\phi_m≤\phi'≤d\phi_m \end{cases} {amin≤vd′≤amax−dϕm≤ϕ′≤dϕm
\qquad 软约束则是通过在目标函数中加入关于控制增量的二次型进行约束,目的是使得目标函数在求取极小值的过程中兼顾到控制增量的最小化。因此上述3.3.节的目标函数则需要修改为
Δ U ^ = a r g min Δ U ^ 1 2 S ~ ^ T Q S ~ ^ + 1 2 ( Δ U ^ ) T P ( Δ U ^ ) \Delta\widehat{U}=arg\min_{\Delta\widehat{U}}{\frac{1}{2}\widehat{ \widetilde{S}}^TQ\widehat{ \widetilde{S}}+\frac{1}{2}(\Delta\widehat{U})^TP(\Delta\widehat{U})} ΔU =argΔU min21S TQS +21(ΔU )TP(ΔU )
\qquad 仅此而已是不够的,我们还需要重写线性状态方程,记
{ G u = [ u ( k − 1 ) − u r ( k ) , u ( k − 1 ) − u r ( k + 1 ) , . . . , u ( k − 1 ) − u r ( k + N − 1 ) ] T E N = t r i l ( o n e s ( 1 , N ) ) (元素均为1的下三角阵) U ~ ^ = G u + T ∗ E N ⋅ Δ U ^ \left \{ \begin{array}{l} G_u=[u(k-1)-u_r(k),u(k-1)-u_r(k+1),...,u(k-1)-u_r(k+N-1)]^T \\ E_N = tril(ones(1,N))\text{(元素均为1的下三角阵)} \\ \widehat{\widetilde{U}}=G_u+T*E_N\cdot\Delta\widehat{U} \end{array} \right. ⎩⎨⎧Gu=[u(k−1)−ur(k),u(k−1)−ur(k+1),...,u(k−1)−ur(k+N−1)]TEN=tril(ones(1,N))(元素均为1的下三角阵)U =Gu+T∗EN⋅ΔU
因此目标函数为
J = 1 2 S ~ ^ T Q S ~ ^ + 1 2 ( Δ U ^ ) T P ( Δ U ^ ) = 1 2 ( A A ⋅ S ~ ( k ) + B B ⋅ U ~ ^ ) T Q ( 1 2 A A ⋅ S ~ ( k ) + B B ⋅ U ~ ^ ) + 1 2 ( Δ U ^ ) T P ( Δ U ^ ) = 1 2 ( A A ⋅ S ~ ( k ) + B B ( G u + T ∗ E N Δ U ^ ) ) T Q ( 1 2 A A ⋅ S ~ ( k ) + B B ( G u + T ∗ E N Δ U ^ ) ) + 1 2 ( Δ U ^ ) T P ( Δ U ^ ) \begin{aligned} J= &\frac{1}{2}\widehat{ \widetilde{S}}^TQ\widehat{ \widetilde{S}}+\frac{1}{2}(\Delta\widehat{U})^TP(\Delta\widehat{U}) \\ =&\frac{1}{2}(AA\cdot \widetilde{S}(k)+BB\cdot\widehat{\widetilde{U}})^TQ(\frac{1}{2}AA\cdot \widetilde{S}(k)+BB\cdot\widehat{\widetilde{U}})+\frac{1}{2}(\Delta\widehat{U})^TP(\Delta\widehat{U}) \\ =&\frac{1}{2}(AA\cdot \widetilde{S}(k)+BB(G_u+T*E_N\Delta\widehat{U}))^TQ(\frac{1}{2}AA\cdot \widetilde{S}(k)+BB(G_u+T*E_N\Delta\widehat{U}))+\frac{1}{2}(\Delta\widehat{U})^TP(\Delta\widehat{U}) \end{aligned} J===21S TQS +21(ΔU )TP(ΔU )21(AA⋅S (k)+BB⋅U )TQ(21AA⋅S (k)+BB⋅U )+21(ΔU )TP(ΔU )21(AA⋅S (k)+BB(Gu+T∗ENΔU ))TQ(21AA⋅S (k)+BB(Gu+T∗ENΔU ))+21(ΔU )TP(ΔU )
令
G A B = A A ⋅ S ~ ( k ) + B B ⋅ G u E N B = T ∗ B B ⋅ E N G_{AB}=AA\cdot \widetilde{S}(k)+BB\cdot G_u \\ E_{NB}=T*BB\cdot E_N GAB=AA⋅S (k)+BB⋅GuENB=T∗BB⋅EN
则
J = 1 2 ( G A B + E N B ⋅ Δ U ^ ) T Q ( G A B + E N B ⋅ Δ U ^ ) + 1 2 ( Δ U ^ ) T P ( Δ U ^ ) = 1 2 G A B T Q G A B + G A B T Q E N B ⋅ Δ U ^ + 1 2 ( Δ U ^ ) T ( E N B T Q E N B + P ) ( Δ U ^ ) ⟹ Δ U ^ = a r g min Δ U ^ J ( Δ U ^ ) s . t . { a m i n ≤ v d ′ ≤ a m a x − d ϕ m ≤ ϕ ′ ≤ d ϕ m \begin{aligned} J=&\frac{1}{2}(G_{AB}+E_{NB}\cdot\Delta\widehat{U})^TQ(G_{AB}+E_{NB}\cdot \Delta\widehat{U})+\frac{1}{2}(\Delta\widehat{U})^TP(\Delta\widehat{U})\\ =&\frac{1}{2}G_{AB}^TQG_{AB}+G_{AB}^TQE_{NB}\cdot\Delta\widehat{U}+\frac{1}{2}(\Delta\widehat{U})^T(E_{NB}^TQE_{NB}+P)(\Delta\widehat{U})\\[2ex] \Longrightarrow &\Delta\widehat{U}=arg\min_{\Delta\widehat{U}}J(\Delta\widehat{U})\\ &s.t.\begin{cases} a_{min}≤v'_d≤a_{max} \\ -d\phi_m≤\phi'≤d\phi_m \end{cases} \end{aligned} J==⟹21(GAB+ENB⋅ΔU )TQ(GAB+ENB⋅ΔU )+21(ΔU )TP(ΔU )21GABTQGAB+GABTQENB⋅ΔU +21(ΔU )T(ENBTQENB+P)(ΔU )ΔU =argΔU minJ(ΔU )s.t.{amin≤vd′≤amax−dϕm≤ϕ′≤dϕm
\qquad 此处参考了友情链接中IEEE的论文的写法,与原书中的写法不一样。这种方法推导出的关于控制增量的目标函数更加直接,也不需要再修改状态向量了。所有MPC的原理讲解部分就到此为止了。
\qquad 完整的MPC函数的MATLAB代码如下:
function u = MPC(Thr_list,ur_list,pSk,u0,L,N,T)
u_max = [20;pi/6];
u_min = [5;-pi/6];
du_max = [2/T;25*pi/180/T];
du_min = -du_max;
A = cell(N,1);
B = cell(N,1);
for i=1:N
Thr = Thr_list(i);
ur = ur_list(:,i);
vdr = ur(1);Phr = ur(2);
A{i} = [1 0 -vdr*sin(Thr)*T;
0 1 vdr*cos(Thr)*T;
0 0 1];
B{i} = [cos(Thr)*T 0;
sin(Thr)*T 0;
tan(Phr)*T/L vdr*T*sec(Phr)^2/L];
end
AA = zeros(3*N,3); % 序列化之后的A
BB = zeros(3*N,2*N); % 序列化之后的B
% S = AA*Sk + BB*u
for i = 1:N
AA(3*(i-1)+1:3*i,:) = eye(3);
for j = 1:i
AA(3*(i-1)+1:3*i,:) = A{j}*AA(3*(i-1)+1:3*i,:);
end
end
for i = 1:N % 列
for j = i:N % 行
BB(3*(j-1)+1:3*j,2*(i-1)+1:2*i) = B{i}; % 3×2
for t = i+1:j
BB(3*(j-1)+1:3*j,2*(i-1)+1:2*i) = A{t}*BB(3*(j-1)+1:3*j,2*(i-1)+1:2*i);
end
end
end
Gu = cell(N,1);
U0 = cell(N,1);
for i = 1:N
Gu{i} = u0 - ur_list(:,i);
U0{i} = u0;
end
Gu = cell2mat(Gu); %2N*2
U0 = cell2mat(U0); %2N*1
EN = zeros(2*N,2*N);
for i = 1:N
for j = 1:i
EN(2*(i-1)+1,2*(j-1)+1)=T;
EN(2*i,2*j)=T;
end
end
ENB = BB*EN;
GAB = AA*pSk + BB*(Gu); % (3N×3)×(3×1)+(3N×2N)×(2N×1)→3N×1
Q = zeros(3*N,3*N);
P = zeros(2*N,2*N);
Qu = [3,3,1]; % 各状态量的加权
Pu = [1,0.2]; % 各控制量的加权
for i = 1:N
Q(3*(i-1)+1:3*i,3*(i-1)+1:3*i) = diag(Qu*1e5*0.9^(i-1));
P(2*(i-1)+1:2*i,2*(i-1)+1:2*i) = diag(Pu*0.9^(i-1));
end
Ab = [EN;-EN]; %4N*2N
umax = cell(N,1);
umax(:)={u_max};
umax = cell2mat(umax); % 2N×1
umin = cell(N,1);
umin(:)={u_min};
umin = cell2mat(umin); % 2N×1
dumax = cell(N,1);
dumax(:)={du_max};
dumax =cell2mat(dumax); % 2N×1
dumin = cell(N,1);
dumin(:)={du_min};
dumin =cell2mat(dumin); % 2N×1
b = cat(1,umax-U0,-umin+U0); % 4N×1
H = ENB'*Q*ENB + P; % 2N×2N
H = 1/2*(H+H'); % 使其严格对称
c = (GAB'*Q*ENB)'; % 2N×1
opt = optimoptions('quadprog','Display','off');
du0 = zeros(2*N,1);
du0(1:2) = (ur_list(:,1)-u0)/T;
for i = 1:N-1
du0(2*i+1:2*i+2) = (ur_list(:,i+1)-ur_list(:,i))/T;
end
du = quadprog(H,c,Ab,b,[],[],dumin,dumax,du0,opt);
u = u0 +du(1:2)*T;
end
Thr_list是车辆朝向角 θ \theta θ的期望值序列,ur_list是车辆的控制量期望值序列,pSk是 S ( k ) − S r ( k ) S(k)-S_r(k) S(k)−Sr(k),u0是 u ( k − 1 ) u(k-1) u(k−1),N是预测时域,L是车长,T是控制周期。
4.仿真示例
仿真动画
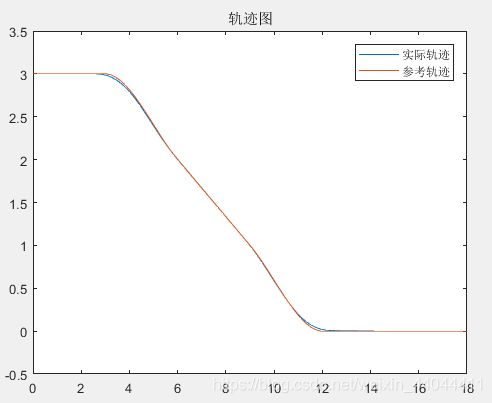
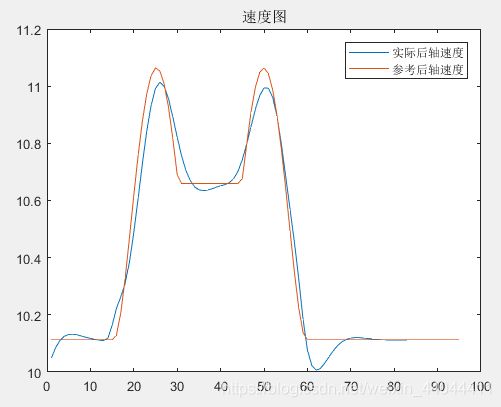
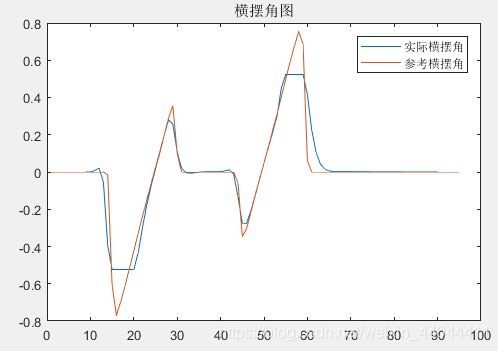
\qquad 可以发现车辆的变道轨迹与期望轨迹基本一致,横摆角成功限制在了-30°~30°之间,速度限幅也符合要求(这里限制上限为20,下限为5)。
\qquad 希望本文对您有帮助,谢谢阅读。本文的完整代码请见第0节友情链接处。