python 多元线性回归_SAS系列34:多元线性回归SAS实践
上一期介绍了多元线性回归分析的基本原理、前提条件和分析步骤,今天我们介绍多元线性回归分析的SAS实现。
四、多元线性回归SAS实现
分析例题:研究血红素(HAEM)与4种微量元素钙(CA)、铁(FE)、铜(CU)、锌(ZN)的关系。
(一)散点图判断变量间的线性趋势
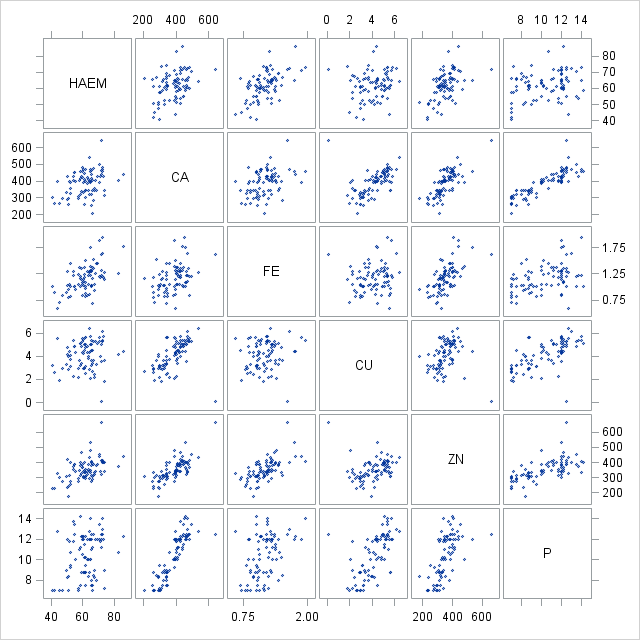
PROC SGSCATTER DATA=REG; PLOT (CA FE CU ZN P)*HAEM/REG;RUN;图11-1 散点图矩阵
图11-1变量HAEM与变量CA、FE、ZN、P存在线性关系,但是变量CA、FE、ZN、P间也存在线性相关。
(二)回归模型拟合
1. 构建CA、FE、ZN、P四个自变量关于因变量HAEM的回归模型
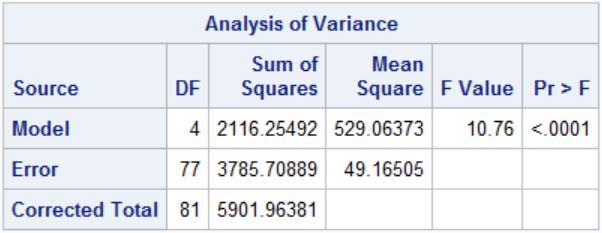
PROC REG DATA=REG; MODEL HAEM=CA FE ZN P/TOL VIF COLLIN DW INFLUENCE;RUN;图11-2 模型假设检验结果
图11-2显示:F=10.76,P<0.0001,拟合的模型有统计学意义。
图11-2 模型的拟合优度信息
图11-2结果显示:决定系数R2为0.3586,表示回归模型能够解释因变量HAEM总变异的35.86%。
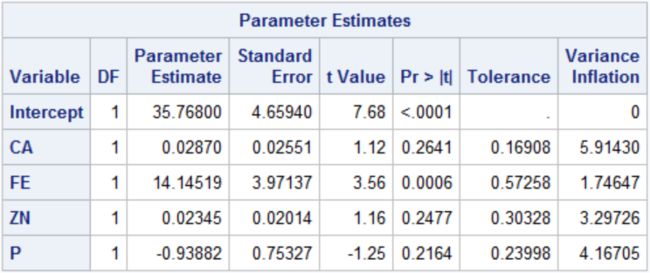
图11-3 回归模型的参数估计结果
图11-3显示了模型回归系数,模型中变量FE的回归系数(t=3.56,P= 0.0006)有统计学意义,其他变量回归系数无统计学意义。
图11-4 模型的多重共线性诊断结果
由图11-3中最后两列分别为容忍度和方差膨胀因子,结果显示CA和P的容忍度较小,其方差膨胀因子较大,表明与其他变量间存在多重共线性;图11-4结果显示条件指数(ConditionIndex)f=36.96979,表明变量间存在严重的内相关性。由最后一行可知,变量CA与变量P间的方差比例值分别为0.95648、0.69567,表明变量CA和P具有较强的共线性。如果一个模型中同时包含这两个变量,得到的结果会很不稳定,甚至产生误导。CA的方差比例大于P的方差比例,可考虑将变量ZN排除模型重新拟合。经两次共线性诊断剔除变量CA和ZN重新构建模型。
2. 构建FE、P四个自变量关于因变量HAEM的回归模型(此处省略详细的SAS结果)
PROC REG DATA=REG; MODEL HAEM= FE P/TOL VIF COLLIN DW INFLUENCE;RUN;结果显示模型假设有统计学意义(F=17.48,P<0.0001),R2=0.3068,模型参数估计结果显示变量FE(t=5.10,P<0.0001),P(t=17.48,P=0.332)。剔除回归系数无统计学意义的变量P,再构建模型。
3. 构建FE四个自变量关于因变量HAEM的回归模型
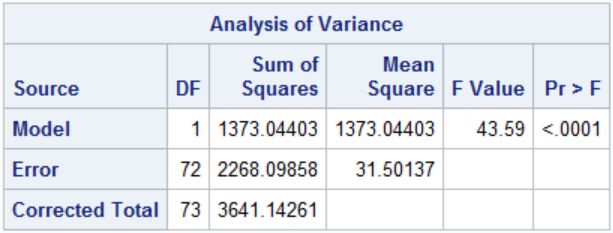
PROC REG DATA=REG; MODEL HAEM= FE /TOL VIF COLLIN INFLUENCE;RUN;图11-5 最终模型假设检验结果
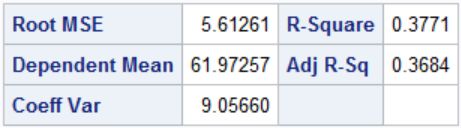
图11-6 最终模型的拟合优度信息
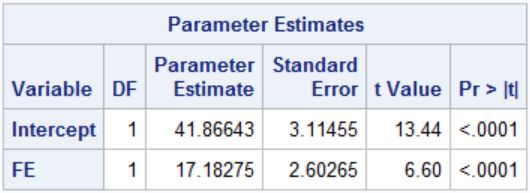
图11-7 最终回归模型的参数估计结果
图11-5至图11-7结果显示模型假设有统计学意义(F=43.59,P<0.0001),R2=0.3771,模型参数估计结果显示变量FE(t=14.33,P<0.0001),P(t=17.48,P=0.332),最终模型的回归方程为HAEM=41.86643+17.182758*FE。
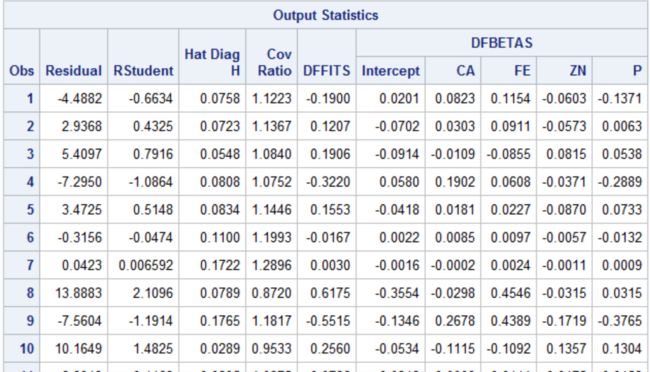
图11-8 最终回归模型的异常点诊断结果
图11-8是对模型的异常点进行诊断,对于结果中的异常个案进行删除后进行分析,本案例经两次诊断共删除8个个案后进行分析,已无异常值。注意在异常值分析时,删除1-2次后,总是有异常值存在,不建议无限地删除下去,否则数据失真,即使模型很好也无法应用。
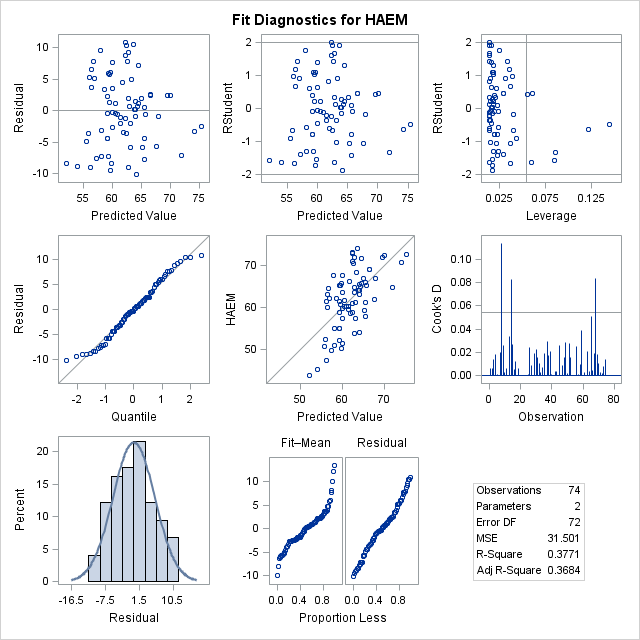
图11-9 最终回归模型的拟合诊断结果
图11-10 最终回归模型的残差图
图11-9是模型拟合诊断结果,判断样本是否满足回归分析的假设条件,以及是否包含强影响点。判断样本是否满足回归分析的假设条件,以及是否包含强影响点。不管是从拟合诊断的残差图(第1行第1列),还是从自变量的残差图(图11-10),残差随机地分布在整个残差图上;从QQ图中,可以判断残差基本服从正态分布。图11-9中的RSTUDENT图、COOK’S D图可判断强影响点。
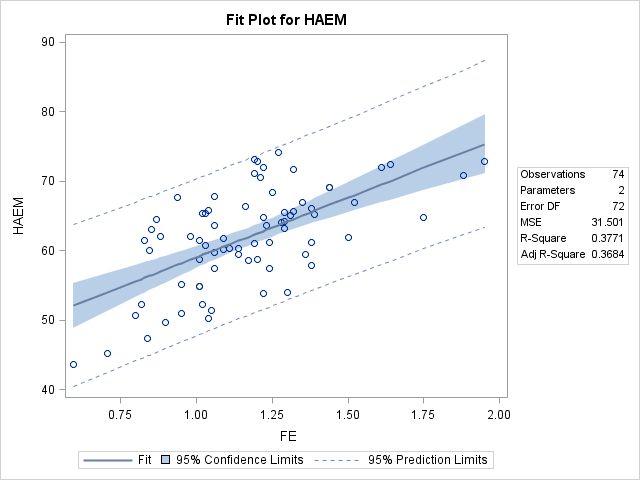
图11-11 新模型拟合结果
图11-11是回归模型的拟合图,拟合图显示了预测的精度,阴影部分是因变量HAEM均值的95%可信区间;两条虚线表示自变量的95%预测区间,即表示自变量FE等于某一值时,HAEM的均值有95%的可能性落在此可信区间内。
五、多元线性回归注意事项
(一)注意事项
(1)多元线性回归的前提条件:线性、独立性、正态性和等方差性,其中线性和独立性非常重要,正态性和方差齐性不是很严格。
(2)多元线性回归需要注意自变量之间的共线性,当存在较为严重共线性时,可以采用逐步回归、岭回归,也可以主成分分析和因子分析进行降维后再进行回归分析。
(3)线性回归分析时样本量一般为自变量的15-20倍,样本量过小模型结果不稳定。
(4)线性回归分析的因变量为连续变量,自变量可以是定量变量也可以是定性变量,当定性变量为多分类时需要设置哑变量。
(5)当线性回归模型应用于自变量对因变量的作用大小解释时,更注重于从专业角度去构建模型,允许存在P>0.05的自变量进入模型,可应用输入法选择自变量;当模型应用于预测时,主要从统计学上构建最佳模型,常用逐步回归法选择自变量。
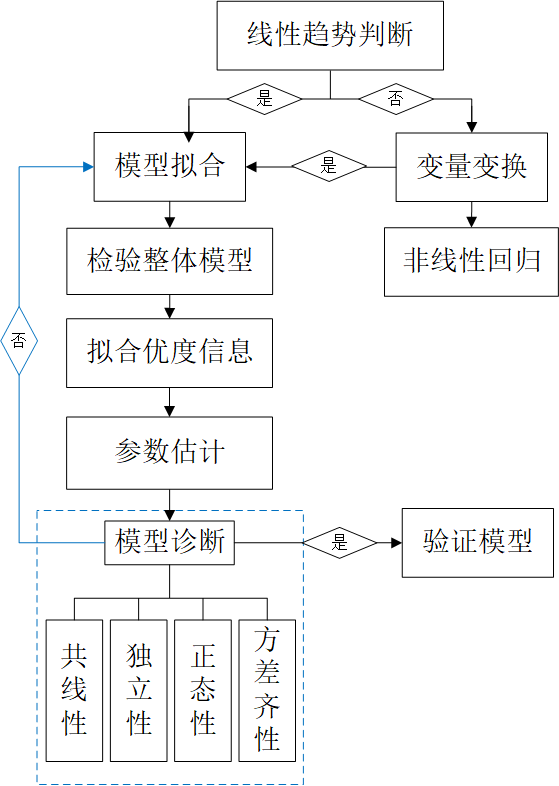
(二)回归分析流程图
图11-12 回归分析流程图
整理不易,欢迎点亮再看哦!
参考文献:
[1] 高惠璇. SAS系统SAS/STAT软件使用手册[M]. 北京:中国统计出版社, 1997.
[2] 孙振球, 徐勇勇. 医学统计学[M].北京:人民卫生出版社, 2014.
[3] 张家放. 医用多元统计方法[M]. 武汉:华中科技大学出版社, 2002.
[4] 武松. SPSS实战与统计思维[M]. 北京:清华大学出版社, 2017.
SAS系列推文
【赠人玫瑰,手留余香】----------------------------------------------
SAS系列33:SAS高级统计(二)多元线性回归
SAS系列32:SAS高级统计(一)
SAS系列31:SAS宏语言(四)
SAS系列30:SAS宏语言(三)
SAS系列29:SAS宏语言(二)
SAS系列28:SAS宏语言(一)
SAS系列27:线性回归
SAS系列26:双变量数据假设检验
SAS系列25:双向有序列联表检验
SAS系列24:单向有序列联表资料的假设检验
SAS系列23:列联表资料假设检验方法
SAS系列22:定性数据假设检验
SAS系列21:SAS统计推断(六)
SAS系列20:SAS统计推断(五)
SAS系列19:SAS统计推断(四)
SAS系列18:SAS统计推断(三)
SAS系列17:SAS统计推断(二)
SAS系列16:SAS统计推断(一)
SAS系列15:SAS数据可视化结果输出
SAS系列14:SAS数据可视化(三)
SAS系列13:SAS数据可视化(二)
SAS系列12:SAS数据可视化(一)
SAS系列11:SAS基础统计过程(三)
SAS系列10:SAS基础统计过程(二)
SAS系列09:SAS 基础统计计算过程
SAS系列08:SAS函数
SAS系列07:SAS数据整理(三)
SAS系列06:SAS数据整理(二)
SAS系列05:SAS数据整理(一)
SAS系列04:SAS数据导入
SAS系列03:SAS入门(二)之SAS编程语言基础
SAS系列02:SAS入门(一)
SAS系列01:统计分析航空母舰-SAS简介
----------------------------------------------
精鼎特邀