*原创文章，转载请注明出处*
在openGL中实现RayPicking
看过D3D入门龙书的朋友肯定知道，第十五章讲picking的时候，是利用拾取射线和包围球的的交叉测试来完成拾取的。但是在OpenGL中，我们知道是利用OpenGL渲染管线的特点，在拾取模式中采用拾取矩阵，然后检查selectbuffer的内容来判断拾取的。这两种方法各有各的好处。在进行OpenGl编程的时候，有时会遇到需要使用拾取射线的时候，下面我就讲一下在OpenGL中如何利用拾取射线来实现picking技术。在你阅读这篇文章之前，首先要明白openGl的渲染管线各个阶段的变换过程，如果你还不清楚，请参考我的另一篇文章《OpenGL渲染管线和坐标变换》。
先来看看picking的时候要进行的步骤，首先我们在屏幕上点击的时候会得到一点屏幕坐标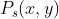
，开始的时候我们可以把深度值初始化位1，于是有
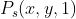。我们点击屏幕上一点的时候并没有深度值Z，所以这里可以设置1。然后用视口变换（viewport transformation）得到在正规化viewport空间中的坐标
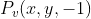，这里我为什么要用-1在后面我会详细说明。这个
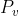就是相机坐标系中的坐标了。现在就可以开始生成拾取射线了，利用直线的参数方程
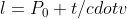，这里
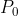就是射线的出发点，t是参数，v是直线的方向。我们一般认为射线是从相机坐标的原点出发的，所以
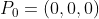,那么用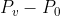
就得到了直线的方向，当然要正规化一下。有了这些信息还够，因为现在物体和射线不在一个坐标中，我们要picking的物体在世界坐标中，而拾取射线是在相机坐标里计算的。所以这里可以把物体转换到相机坐标，也可以把射线转换到世界坐标。为了和龙书上对应，这里我们将射线转换到世界坐标。然后在世界坐标里进行包围球和该射线的测试就可以了。下面我一步一步来详细说明。
1. 屏幕坐标到视口空间坐标的变换(Screen coordinate to viewport coordinate)
也许这里叫视口坐标有点不准确，反正它就是一个物体的顶点被投影后的坐标。因为被投影后的物体坐标是被正规化的，它在区间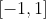
之间。一个800*600大小的屏幕上的坐标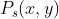要如何转换到-1到1之间的坐标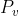呢？
在上面的图中我们可以找到一个关系，
其中的ScreenWidth和ScreenHeight分别是窗口的宽和高。比如我们800*600窗口的正中点击了一下，屏幕坐标为(400,300)，带入上面公式即可得到投影后坐标为(0,0)。
2. 投影坐标到相机坐标系坐标(Viewport coordinate to Carmera coordinate)
由于投影后的坐标是经过投影矩阵处理过的，它的大小已经被缩放了。所以这里我们要的到投影矩阵中关于x成分和y成分的比例，在openGL中我们可以通过 glGetDoublev(GL_PROJECTION_MATRIX，m)这个函数来得到当前投影矩阵的数据，m是用来保存这些数据的地址。由于OpenGL的矩阵是以列的形式来保存的，所以对于x成分和y成分的就分别为m[0]和m[5]，用上面得到的坐标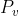分别除以这两个值。
这里是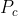
就是窗口上一点对应的在相机坐标系中的坐标了，由于要计算射线的方向，就要加上z值。在这篇文章开始的时候我就提到了，射线的起点就是相机坐标的原点，但是还需要一个点来决定射线的方向。OpenGL由于使用右手坐标系，Z轴是朝向外的，Z轴的方向关系到我们射线的方向，如果Z为正那么射线是朝向屏幕外，如果Z为负，那么射线是朝向屏幕里，这里就要根据时的需要改变射线的方向。如果相机是朝向Z轴负方向的，那么这里Z要为负数才可以。后面的例子程序中相机是朝向负方向的，所以这里我们把Z值设定为-1。于是有
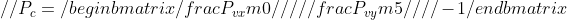
有了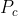我们就可以生成拾取射线，只需要2个变量即可。一个用来保存射线的方向，一个用来保存射线的起点。
3. 把射线从相机坐标转换到世界坐标(Carmera coordinate to world coordinate)
如果使用了函数gluLookAt的话，那么我们需要把相机坐标系转换到世界坐标系。如果没有设置过相机位置，那么不用转换，因为默认状态时相机坐标和世界坐标重合的。该函数的第一个参数是表示相机的位置，如果相机没有转动之类的，那么只要使用表示相机位置的参数就可以了。
这里x，y，z就分别表示相机在世界坐标中的位置。如果相机有转动，那么该矩阵的前三列就要有变化，具体怎么变化请各位读者自己想想，呵呵。这里我就不详细说明了。有了从相机坐标系到世界坐标系的变换矩阵，那么用这个矩阵
乘以射线的方向和射线的起点就可以把射线转换到世界坐标了。要注意的是，这里射线的起点和方向要用其次坐标系来表示。
这样我们就把射线转换到世界坐标了。下面就是交叉测试了。
4. 世界坐标中的射线和球的交叉测试
先来看看下面的图
如果绿色包围球圆心坐标为C(a,b,c)，半径为R的话，那么球的方程可以表示为：
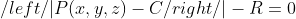
P表示球上的点，如果P点在球上的话，那么P点到球的距离肯定等于球的半径R。于是有上面的等式成立。射线上t1时刻和t2时刻表示和球相交的点，如果射线和球相交，那么这2个点肯定也满足球的方程，于是t时刻射线上的点带入到球方程中，可以得到
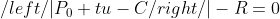
展开上式整理一下，得到二元一次方程组，可以写成下面的形式
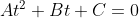
其中
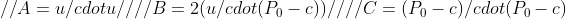
这里u是射线的方向，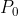
是射线的起点，c是球心坐标。如果射线和球相交，那么上面的方程组就有1个或2个解，当然射线和球相切的时候有2个相同的解。现在根据球根公式就可以判断射线和包围球是否相交了。解出t1，t2分别为：
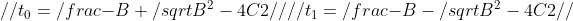
这里没有A = 1，是因为u已经单位化了。
在OpengL中实现picking的过程就完了，其实不难。只要熟悉渲染管线，那么这些都很好理解。下面是源代码，需要的同学可以参考。注意，代码中的Gvector，Gvector3，GMatrix是我自己的数学类，表示向量和矩阵的操作。同学们可以自己实现。例子程序运行如下。
程序代码
/* 代码中的Gvector,Gvector3等等相关的类是我自己 实现的向量操作类。运行该程序时请大家自己对该 程序修改一下，用自己的向量类或就是数组表示 */ #include #include #include #include #include int WIDTH = 800; int HEIGHT = 600; //定义包围球的结构体 struct boundingsphere { GVector c; //球心在世界坐标中的位置 double r; //半径 }; //定义射线结构体 struct Ray { GVector pos; //射线起始位置 GVector dir; //射线方向 } PickingRay; // 定义一个射线 boundingsphere b={GVector(4), 1.5}; //定义一个包围球,半径为1.4 //屏幕坐标到投影后坐标的转换 GVector3 screen2viewport(int x, int y, int w, int h) { double _x = 2.0*x/w -1; double _y = 1-2.0*y/h; return GVector3(_x,_y, 1.0); } //投影坐标到相机坐标的转换 GVector3 viewport2viewspace(GVector3 vp) { GLdouble m[16]; glGetDoublev(GL_PROJECTION_MATRIX, m); double _x = vp[0]/m[0]; double _y = vp[1]/m[5]; return GVector3(_x,_y, -1.0); } //生成拾取射线 Ray computeRay(GVector3 s, GVector3 e) { Ray ray; ray.dir = GVector(4, e[0]-s[0],e[1]-s[1], e[2],-s[2], 0.0).Normalize(); ray.pos = GVector(4, s[0],s[1],s[2], 1.0); return ray; } //将拾取射线从相机坐标转换到世界坐标 void ray2world(Ray *ray) { // 这里最后一列为(0,0,5,1)是因为相机的位置在世界坐标的(0,0,5)这个地方 double m[16] = { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 5, 0, 0, 0, 1 }; GMatrix M(4,4,m); ray->pos = M * ray->pos; //矩阵乘以点 转换射线起始坐标到世界坐标 ray->dir = M * ray->dir; //矩阵乘以向量 转换射线方向到世界坐标 } //判断是否相交 bool intersect(Ray r, boundingsphere b) { double A = r.dir*r.dir; double B = 2*r.dir*(r.pos - b.c); double C = (r.pos - b.c)*(r.pos-b.c) - b.r*b.r; //根号内部分为0,那么肯定无实数解,说明射线和球不相交 if(B*B-4*C <0) return false; double x1 = (-B + sqrt(B*B-4*C) )/ (2.0); double x2 = (-B - sqrt(B*B-4*C) )/ (2.0); //如果有解,且有一个大于0,说明射线和球相交,小于0的话说明射线的反方向和球相交 if(x1 >= 0 || x2 >=0) return true; return false; } void glinit() { glEnable(GL_DEPTH_TEST); glEnable(GL_LIGHTING); glEnable(GL_LIGHT0); } void render() { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT ); glClearColor(1.0,1.0,1.0,1.0); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); //设置相机的位置 gluLookAt(0.0,0.0,5.0, 0.0,0.0,0.0, 0.0,1.0,0.0); float m[16]; GLfloat diff[]={1.0,.0,.0,0.7}; GLfloat amb[]={1.0,.0,.0,0.6}; GLfloat sp[]={1.0,1.0,1.0,0.5}; glMaterialfv(GL_FRONT, GL_DIFFUSE, diff); glMaterialfv(GL_FRONT,GL_AMBIENT,amb); glMaterialfv(GL_FRONT, GL_SPECULAR, sp); glMateriali(GL_FRONT, GL_SHININESS, 64); static float a = 0.0; static float r = 0.0; //将物体和包围球一起移动 glTranslatef(r*cosf(a), r*sinf(a), -8.0); b.c.Set(r*cosf(a), r*sinf(a), -8.0,1.0); glutSolidTeapot(1.0); GLfloat d[]={1.0,1.0,0.0,0.3}; glMaterialfv(GL_FRONT, GL_DIFFUSE, d); //渲染包围球 glEnable(GL_BLEND); glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); glutSolidSphere(b.r,20,20); glDisable(GL_BLEND); glGetFloatv(GL_MODELVIEW_MATRIX, m); glMatrixMode(GL_PROJECTION); glGetFloatv(GL_PROJECTION_MATRIX, m); a += 0.02; r += 0.005; if(r>=5) r=0; if(a>=3.14*2) a=0; glutSwapBuffers(); glutPostRedisplay(); } void resize(int w, int h) { glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(45, (double)WIDTH/HEIGHT, 0.1, 1000); glViewport(0,0,w,h); glMatrixMode(GL_MODELVIEW); WIDTH = w; HEIGHT = h; } void mouseDown(int btn, int state, int x, int y) { if(btn == GLUT_LEFT_BUTTON && state == GLUT_DOWN) { //屏幕坐标转换为投影后坐标,保存在v1中 GVector3 v1 = screen2viewport(x,y, WIDTH, HEIGHT); //将投影坐标v1转换为相机坐标,保存在v2中 GVector3 v2 =viewport2viewspace(v1); //利用相机坐标生成拾取射线 PickingRay = computeRay(GVector3(.0,.0,.0), v2); //将射线转换到世界坐标 ray2world(&PickingRay); //判断是否和包围球相交 bool is =intersect(PickingRay, b); if(is) MessageBox(0,"Picked!","message",0); } } int main(int argc, char**argv) { glutInitDisplayMode(GLUT_RGB|GLUT_DOUBLE|GLUT_DEPTH); glutInitWindowSize(WIDTH,HEIGHT); glutCreateWindow("PickingRay"); glinit(); glutMouseFunc(mouseDown); glutDisplayFunc(render); glutReshapeFunc(resize); glutMainLoop(); return 0; }
*原创文章，转载请注明出处*
