机器学习之神经网络

目录

一、引言

 二、人工神经网络基础

1、M-P神经元模型

2、前馈神经网络及其规律

三、误差逆传播算法

1、损失函数

Delta学习规则

前馈神经网络的目标函数

2、“修正”策略

①梯度下降法

②动量法SGDM

③Adagrad法

3、“修正”行为

①输出层权重改变量

②隐含层权重改变量

③举个例题

四、避免“过拟合”

1、添加数据

2、简化模型

3、早期停止训练

 4、权重衰减

5、Dropout

---

一、引言

        不知不觉我们今天要开始研究深度学习的基础内容了。而有关深度学习的内容，比前面几次课的机器学习算法（比如说贝叶斯分类器和决策树）听起来更为“玄学”与模糊。但是小编相信各位读者能耐着性子读下去，进步的飞快！

        在讲解神经网络之前，我们得先理解深度学习与神经网络的关系是怎样的。

        深度学习(Deep Learning)是一种基于无监督特征学习和特征层次结构的学习方法，它也被称为特征学习或无监督特征学习。深度学习的实质，是通过构建具有很多隐层的机器学习模型和海量的训练数据，来学习更有用的特征，从而最终提升分类或预测的准确性。 也就是说“深度模型”是手段，“特征学习”是目的。学习深度学习要具备一定的神经网络知识：一般需先学习掌握传统的人工神经网络 (主要有感知器、BP神经网络等) 的基础知识，再学习研究“深度学习”相关部分。

        所以，我们学神经网络相关知识，说白了就是为深度学习铺路。那么带着这一层目的，我们开始今日份学习！

 二、人工神经网络基础

1、M-P神经元模型

        相信很多同学刚开始接触人工智能时，就听到过类似于“仿真”、“神经网络”之类的词语。而神经网络，自然仿真的就是我们大脑中神经元所构成的“网络”。我们先来学学微观模型。请看下图，我们暂且将这三个神经元称之为左神经元、右神经元以及下神经元：

         在高中生物课上，我们学习过：每个神经元与其他层的神经元相连，当前面的神经元（比如说左神经元与右神经元）“兴奋”时，就会释放神经递质，向后面的神经元（比如说下神经元）“表达”这种兴奋，改变它的电位。而这种电位超过了某一阈值时，它会被“激活”，紧接着也会变得兴奋，以此类推继续向后面的神经元“表达”自己的兴奋。

        那么，用计算机与数学的语言，如何去描绘后面这个神经元的状态呢？假设左神经元因为兴奋,电位为，它的电位与神经递质的转换比为（单位电位能产生个神经递质）。且释放的神经递质中，占比的能抵达下神经元，神经递质与电位转换比为（也就是一个神经递质能产生的电位）。右神经元因为兴奋，电位为，它的电位与神经递质的转换比为，且释放的神经递质中，占比的能抵达下神经元，神经递质与电位转换比为。下神经元的电位阈值为。所以此时下神经元的状态为。其中f为激活函数，有一种是sgn函数：当自变量小于0时，f为0，表示它不兴奋；当自变量大于0时，它等于1，表示此时它很兴奋。

        看起来很复杂对不对？其实计算机科学家在考虑神经网络时，并不会想那么多。他们可以用权重w代替掉、v、三者的乘积，而把x当做是输入。而当前神经元有n个时，我们能得到更具有普遍意义的公式：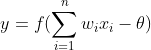

2、前馈神经网络及其规律

        学完了微观的神经元输入输出原理，我们再来看看宏观的神经网络。神经网络是由大量神经元节点按一定体系架构连接成的网状结构，一般都有输入层，隐含层和输出层。传统的浅层网络，一般有3~5层，如下图。前馈神经网络遵循自己的规律，我们以下图的A、B、C神经元为例描述这些规律。

        规律1：前馈神经网络，是人工神经网络的一种，各神经元从输入层开始，接收前一级输入，并输出到下一级，直到输出层。 其中第一层称为输入层，最后一层为输出层，中间为隐含层。隐含层可以是一层，也可以是多层。

        规律2：整个网络中无反馈，可用一个有向无环图表示。（也就是说神经元C所在的这一层可以通向神经元A所在的这一层，而神经元A所在的这一层无法通往神经元C所在的这一层）

        规律3：前馈神经网络采用一种单向多层结构。其中每一层包含多个神经元，同一层的神经元之间没有相互连接，层间信息的传送只沿一个方向进行。（举个例子：同层的神经元A与神经元B没有连接）

   

三、误差逆传播算法

1、损失函数

Delta学习规则

        delta学习规则是一种有监督的学习方法，该算法根据神经元的实际输出与期望输出差别来调整连接权，其数学表示如下：                                 

        代表神经元j到神经元i的连接权重增量，是神经元i的期望输出，是神经元i的实际输出，表示神经元j的状态，a是表示学习速度的常数，基于此思想规则，我们定义了前馈神经网络的目标函数。

前馈神经网络的目标函数

        对于一系列的训练样本x，期望输出向量t=（……），网络实际输出向量y=(……),对于传统BP算法，它的目标函数（损失函数）为,也就是各个输出误差的平方之和的一半。常见的目标函数还有均方差函数、交叉熵函数等等，不过下述文章均以J（w）为例。

        我们自然是期望通过调整各个神经元之间的权值w来使这个损失函数达到最小。最好的情况是损失函数为0，代表着期望值与实际输出值完全一样，预测的特别准。但实际上很难达到100%预测正确，所以需要我们不断地调整权值，使目标函数向0逼近。所以我们提出了很多“修正”策略。

2、“修正”策略

①梯度下降法

        梯度下降法（简称GD）是我们计算函数极值的一种方式，我们会先选择一个初始点，将该点按照梯度下降的方向进行调整，就会使得J（w）往更低的方向进行变化，直到无法下降为止。如公式所示：

w（m+1）表示新权值，w（m）代表旧权值。代表步长，代表着我们期待往修正方向走多远，它还有一个名字叫做学习率，一般该参数会被科学家给定，不是我们初学者所能考虑的。

        为了让大家能够更好的理解梯度下降法，不如一起编个程，做个题目：

请用梯度下降法求出函数的极小值。（已知学习率为0.1，初始值为（3,2），迭代100次）

import math

# 原函数
def Z(x,y):
    return 3*(x-1)**2 + y**2 +math.exp(x+y)
# x方向上的梯度
def dx(x,y):
    return 6*x-6+math.exp(x+y)
# y方向上的梯度
def dy(x,y):
    return 2*y+math.exp(x+y)
# 初始值
X = x_0 = 3
Y = y_0 = 2
# 学习率
alpha = 0.1
# 迭代30次
for i in range(100):
    temX = X - alpha * dx(X,Y)
    temY = Y - alpha * dy(X,Y)
    temZ = Z(temX, temY)
    # X,Y 重新赋值
    X = temX
    Y = temY
    # 将新值存储起来
    print(u"第"+str(i+1)+"次：学习率为"+str(alpha)+"    X为"+str(X)+"    Y为"+str(Y))

output=Z(X,Y)
print("最终结果为"+str(output))

最终结果在1.7左右 

        对于机器学习来说，梯度下降法又可以细分为三类：

        每次使用整个数据集计算损失后来更新参数的方法，我们称为GD，它的计算很慢，占用内存大且不能实时更新，优点是能够收敛到全局最小点，对异常数据不敏感。

        每次更新度随机采用一个样本计算损失来更新参数的方法我们称为SGD，它的计算比较快，占用内存小，可以随时新增样本。这种方式对于样本中的异常数据敏感，损失函数容易震荡。容易收敛到局部极小值，但由于震荡严重，会跳出局部极小，从而寻找到接近全局最优的解。

        为了解决上述二者的缺点，我们将GD和SGD结合在一起，每次从数据集合中选取一小批数据来计算损失并更新网络参数，这种方法称为BGD。

②动量法SGDM

        这一方法模拟的惯性，下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。类似于一个小球从山坡上滚下，它的前进方向由梯度与之前的下降方向(momentum)共同决定，不只被梯度制约。SGDM不仅克服了之前SGD陷入局部最小值后得到非最优解的缺点，在落入局部最小值点时可以走出去，而且有效的防止了SGD可能造成的震荡问题。

③Adagrad法

        Adagrad 是适应性学习率算法，基本思想是对每个变量用不同的学习率，这个学习率在一开始比较大，用于快速梯度下降。随着优化过程的进行，对于已经下降很多的变量，则减缓学习率，对于还没怎么下降的变量，则保持一个较大的学习率。就好比如果我们下坡的时候想下降的最快，那么面对陡坡，我们选择大步子会让自己下降的更快，而对于不陡的坡则迈小步子。

3、“修正”行为

        接下来的“修正”行为，均是使用梯度下降法。

①输出层权重改变量

        我们了解了梯度下降法的思路后，现在的问题逐步转化为了如何求，即如何求解目标函数对权值的梯度。

        我们先来算算输出层的权重改变量为多少。先定义一个函数，这个函数代表着隐含层对输出层中某一个神经元的总输入。

        那么J对隐含层中某个神经元到输出层的权重w求的偏导可以修改为

        而众所周知，右边部分的，而左边部分可以等价代换为，其中，也就是说剩下一个需要自行求解的，仔细观察，想想我们刚刚学过的M-B神经元模型，我们发现它的值竟然为激活函数的导数！

②隐含层权重改变量

        还是同样的道理，先定义一个函数。那么，依据我们刚刚求输出层权重改变量的思路，它可以拆解为，剩下的步骤与上面的如法炮制，读者们可以自行求解一下。

 

③举个例题

        如果您大抵能够听懂，我们不妨来做一个题巩固一下求解思路。考虑到我们是以捋清楚思路为主，而非考计算，请读者们掏出自己的计算器完成。

假设有如下神经网络，各层相连接的神经元之间的参数如图所示，已知步长为1，实际输出值为0.5，激活函数为sigmod函数，即，请求出v1、v2经过梯度下降法修改后的值。

        一步一步来，我们先求出各个神经元的输入P的输入为，Q的输入为，那么P的输出为，Q的输出为，y的输入为，所以实际输出与期望输出之差为0.148。而sigmod函数又有这样一个性质，借助这个性质能简化我们的计算量，即的变化量为=0.555*0.648*（1-0.648）*0.148=0.0187，新的权重为=0.3-0,0187=0.283，同理的变化量为=0.632*0.648*(1-0.648)*0,148=0.0213，新的权重=0.7-0.0213=0.6787。

四、避免“过拟合”

        当权重参数太多，而样本不足的时候，神经网络可以采用下列方法避免过拟合。

1、添加数据

        增加的数据必须是符合要求的实验数据，即与已有数据是独立同分布的。常见的数据扩增方式：采集更多数据、扩增原始数据、数据重采样、生成虚拟数据等等。

2、简化模型

        不断降低模型的复杂度，最终达到一个平衡状态：模型足够简单以至于不会发生过拟合，又足够丰富可以从数据中学习到规律

3、早期停止训练

        训练时，当每次Epoch结束时在验证集上进行测试，如果随着Epoch次数的增加发现误差在上升，那么就提前结束训练，将此时的权重作为网络的最终参数。如下图红色的这条竖线，代表着从这里开始停止。

 4、权重衰减

        有些位置的权重是无用的，我们可以使用权重衰减公式 , 为衰减率，大概在0.01左右，能够有效的减少连接。

5、Dropout

        在训练过程中随机让神经元失活或让网络中的连接无效，每次训练忽略的神经元或连接是不同的，让神经网络没机会过度依赖。本质上Dropout就是用一小块数据来训练一系列的子网络。

        那么，能颇具耐心的一点一点读到这里，我只能说各位都太优秀了，为自己鼓个掌吧！你的坚持学习必然会得到回报的！

        小编接下来还有各方各面的文章，感兴趣的友友可以给我点个赞后再离开吗，小编在此鞠躬感谢啦！