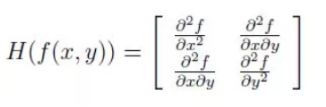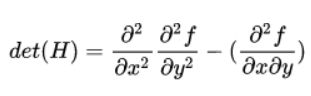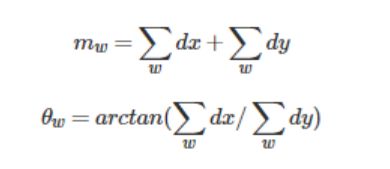图像特征描述子（二）——SIFT、SURF

本文主要参考文章：1.【动手学计算机视觉】第七讲：传统目标检测之SIFT特征 - 知乎

                                 2. SIFT特征匹配详细原理_南洲.的博客-CSDN博客_sift特征

                                 3.Sift算子特征点提取、描述及匹配全流程解析_牧野的博客-CSDN博客

                                 4.sift计算描述子代码详解_浅谈SIFT特征描述子_weixin_39564527的博客-CSDN博客

                                 5.SIFT特征提取分析 - 一只有恒心的小菜鸟 - 博客园

                                 6.SIFT特征匹配算法介绍——寻找图像特征点的原理_Suray_Fu的博客-CSDN博客_sift特征匹配算法

                                7.Sift中尺度空间、高斯金字塔、差分金字塔（DOG金字塔）、图像金字塔_牧野的博客-CSDN博客_高斯差分金字塔

                                8.SIFT特征 - 简书

                                9.opencv3 中的 SIFT 用法_第五篇-CSDN博客_opencv sift

                                10.OpenCV2 特征检测与匹配_Johnnan002的博客-CSDN博客

                                11.图像拼接（十三）：OpenCV拼接多幅图像(以中间图像为参考)_czl389的专栏-CSDN博客_opencv多张图片拼接

                                12.opencv中match与KnnMatch返回值解释_冯邵封的博客-CSDN博客_knnmatch

                                13.SURF到底比SIFT快在哪里？_视觉小新的博客-CSDN博客

                                14.SURF算法_知识搬运工的博客-CSDN博客_surf算法

                                15.SURF特征提取分析（一）_李丽的博客-CSDN博客

                                16.数字图像处理之积分图 - 知乎

特征描述子是图像的简化表示，仅包含图像的最重要信息。本博客将介绍几种常用的特征描述子，包括HOG、SIFT、SURF、ORB.一般认为：性能上SIFT>SURF>ORB,速度上完全相反。

目录

2.SIFT(Scale-invariant feature transform,尺度不变特征变换)

2.1主要思想

2.2适用领域

2.3SIFT特征提取和匹配过程

2.4opencv SIFT描述子的调用及计算

3.SURF（Speeded Up Robust Features，加速稳健特征）

3.1与SIFT的关系

3.2SIFT特征提取和匹配过程

3.3opencv SURF描述子的调用及计算

---

2.SIFT(Scale-invariant feature transform,尺度不变特征变换)

2.1主要思想

       计算机没有主观意识去识别哪些是特征点，它能做的，只是分辨出变化率最快的点。而且当图像放大或者缩小时，它读取的特征点与原先可能差异，所以其中一个办法就是把物体的尺度空间图像集合提供给计算机，让它针对考虑不同尺度下都存在的特征点。

        SIFT算法的实质是在不同的尺度空间上查找关键点（特征点），计算关键点的梯度幅值大小、方向、尺度，利用这些信息对特征点进行描述的问题。Sift所查找的关键点都是一些十分突出，不会因光照，仿射变换（仿射变换包括平移、旋转、缩放、拉伸，缩放指的同比例缩放，拉伸就是不同比例的缩放，在我的测试中SIFT对拉伸的稳定性比较有限）和噪声（一定程度上）等因素而变换的“稳定”特征点，如角点、边缘点、暗区的亮点以及亮区的暗点等。

2.2适用领域

        该算法在目标检测和特征提取方向占据着重要的地位。

2.3SIFT特征提取和匹配过程

        输入图像-》图像灰度化-》构建尺度空间-》空间极值点检测-》稳定关键点的定位-》稳定关键点方向信息分配-》关键点描述-》特征点匹配

具体描述步骤前，其中涉及的一些预备知识也是在我理解中最困难的点：

（1）尺度空间的构建本质上由尺度空间和图像金字塔结合起来，一系列的下采样操作以及不同的平滑核对图像的平滑。平滑核是在每一组（Octave）中的每一层（S层）都在变化的，每一组Octave的尺度变化范围为,第t组（Octave）的尺度范围[，下采样只在每个Octave（除去第一个octave）的第一层（即底层）使用。第t+1个（Octave）的第一幅图像由上层塔的（t+1）尺度下（即第t个Octave的第s层）的下采样得到。也就是说同组内，它们的尺寸是一样的。

（2）要找到图像在不同尺度下的关键点

（3）在图像匹配时，对两幅图像分别提取sift特征，取图像1中某个关键点，并在图像2中的所有关键点中（各个尺度上）找到与其距离最近的关键点

具体步骤描述：

1.图像灰度化：可选操作，一般都以灰度图作为处理对象。

2.构建尺度空间：尺度空间构建的基础是DOG金字塔、DOG金字塔构建的基础是高斯金字塔。

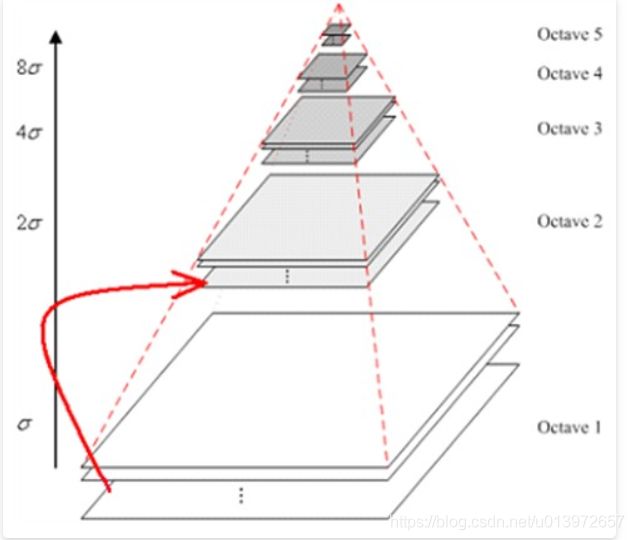
构建金字塔图像如下（下图来源于链接5，为便于理解复制在此处，如有侵权联系笔者删除）：

高斯金字塔的构建：将金字塔分成O组，每一组称为一个Octave；每一个Octave又分成S层，每层的图像是由不同方差的高斯滤波器滤波的结果，在同一Octave内，每层图像的尺寸是一样的，后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍；每一个Octave的底层图像由上一个Octave的第S层图像高宽下2采样得到（缩小1/4）。给定一组（O，S）可以唯一确定高斯金字塔中的一幅图像，同一组octave图像的模糊度逐渐变大（平滑的参数逐步变大），能够模拟人在距离目标由近到远时目标物体在视网膜上的形成过程。

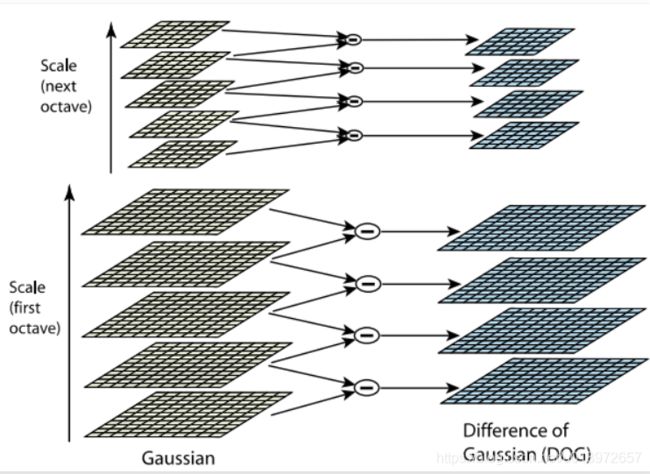
DOG金字塔的构建：对高斯塔相邻两层做差得到DOG响应金字塔。

对于第i个（i=1...）Octave的第n层（n=1...S）图片，其对应的高斯尺度为,其中k=

在实际应用中，为了保证上一组Octave与当前Octave的连续性，需要对每Octave的顶层再加3层。

假设S=3，对第1个Octave，gauss塔尺度为σ, kσ, k2σ, DoG塔尺度为σ, kσ，而DOG空间中的极值比较需要3层（因为SIFT尺度检测对每个点检测需要比较相邻的26个点位于3层中），因此考虑加上3层，这样第1个Octave的DOG空间尺度为 σ, kσ, k2σ, k3σ,k4σ，第2个Octave的DOG空间尺度为 2σ, 2kσ, 2k2σ, 2k3σ, 2k4σ，进行极值比较时底层和顶层无法计算，可以选择DoG space中的中间三项kσ,k2σ,k3σ，那么下一octave中DoG space所得三项即为2kσ,2k2σ,2k3σ，其首项2kσ=。刚好与上一octave末项k3σ=尺度变化连续起来，所以每次要在Gaussian space添加3项，每组（塔）共S+3层图像，相应的DoG金字塔有S+2层图像。

高斯金字塔的效果如下，分别是第一组的4层和第二组的4层（本图摘自链接7，为便于理解放于此处，如有侵权联系笔者删除）：

另外读博客7中写道“在不同组内，后一组第一个图像是前一组倒数第三个图像的下二分之一采样”，我在整理时由“每一个Octave的底层图像由上一个Octave的第S层图像高宽下2采样得到（缩小1/4）”及“为了保证上一组Octave与当前Octave的连续性，需要对每Octave的顶层再加3层”这两句综合考虑，其实时应该实际中说的是：后一组图像是前一组图像（加3之后的）倒数第四个图像的下二分之采样吧！（个人理解，如果有误，还望各位大佬指点迷津）

3.空间极值点检测

        SIFT尺度空间的极值检测在DOG塔里进行，对每个点，比较其相邻的26个点，若为最大或最小值则记为待选极值点。如下图（本图摘自链接8，为便于理解放于此处，如有侵权联系笔者删除）。在同一组中的相邻尺度之间进行寻找。

4.稳定关键点的定位

       这个部分有很多的数学推理（详细可看参考链接8和链接5）,DOG值对噪声和边缘比较敏感，所以在第2步的尺度空间中检测到的局部极值点还要经过进一步的筛选，去除不稳定和错误检测出的极值点，包括对图像进行非极大值抑制，去除对比度较低的点以及通过Hessian矩阵去除边缘的点。另一点就是在构建高斯金字塔过程中采用了下采样的图像，在下采样图像中提取的极值点对应在原始图像中的确切位置，也是要在本步骤中解决的问题。

5.稳定关键点方向信息分配

        上一步在DoG空间中已经找到关键点，可以使用三元组（x,s,）表示关键点，其中三个值分别表示关键点的位置、尺度和方向。计算特征点的方向是为了使特征描述子具有旋转不变性。

样本点的方向（其实就是对应尺度图像上对应位置的梯度），关键点的方向由以关键点为中心的邻域（16*16）内的所有样本点的梯度值和方向来统计得到，具体的，将（16*16）分为16个区域分别统计四个梯度直方图，每个4*4的区域形成一个8bin的直方图，其中一个bin代表45度,bin中的值根据幅值及高斯下降函数（根据距离中心的远近）调节权重来确定，计算每个样本点该尺度下x方向的梯度Gx及y方向的梯度Gy。根据它们确定关键点的方向和幅值

梯度方向（角度的值）=atan(Gy/Gx)

梯度幅值=

直方图中的峰值就是主方向，其他的达到最大值80%的方向可作为辅助方向。如下图（本图摘自链接8，为便于理解放于此处，如有侵权联系笔者删除）：

6.关键点描述

为了使描述子具有旋转不变性，一般将图像旋转使关键点的方向统一对齐到图像x轴的方向。

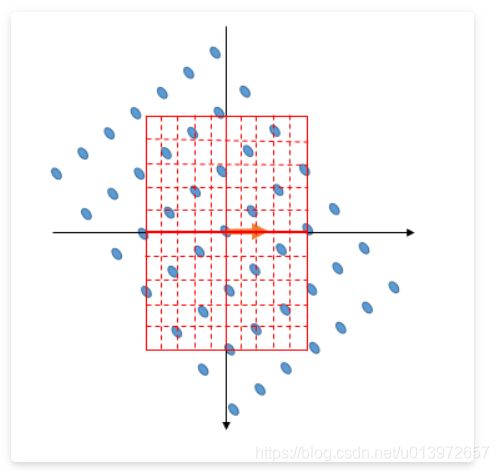
看一个示意图蓝色的点表示该尺度图像中的像素点，红色方格表示子区域（意思代表上一部分的16*16的邻域）箭头表示计算出的关键点方向（下图摘自链接5，为便于理解放于此处，如有侵权联系笔者删除）：

将其旋转为与x轴同向如下图（下图摘自链接5，为便于理解放于此处，如有侵权联系笔者删除）：

此时再对旋转后的图像上取关键点的16*16领域计算描述子。

由上一步可知每个4*4的小块有8个bin,则16*16的块共有(16*16)/(4*4)*8=128维的描述子v=[a1,a2,a3,...a128]，为去除光照影响，通常会对描述子进行归一化：

计算平方和的根：k=

并将向量v中的每个值除以此值k:

归一化后的向量=（a1/k,a2/k,a3/k,...,a128/k）

7.特征点匹配

        在图像匹配时，对两幅图像分别提取sift特征，取图像1中某个关键点，并在图像2中的所有关键点中（各个尺度上）找到与其距离最近的关键点

几种简单计算匹配的方法：

（1）直接欧式距离判断。

（2）最近邻次近邻匹配。如果某个特征点与最相近（描述子最相像）的一个特征点和次相近的特征点差不多，就不太好；如果差很多，也就是和最相近的特征点很相近，和次相近的特征点不太相近的话就说明和最相近的特征点匹配很好。

（3）RANSAC匹配筛选，主要使用了findHomography函数。

（4）GMS匹配筛选,原来写的一篇里简单叙述了使用方法并且给出了源码链接，附上地址

GMS图像特征匹配学习简要记录_u013972657的博客-CSDN博客

（5）还可以对局部描述子进行聚合编码，包括特征袋BOF、Fisher向量以及VLAD等

2.4opencv SIFT描述子的调用及计算

 opencv2与opencv3中SIFT的使用方法是不同的，opencv3要使用SIFT需要先cmake编译。此处展示opencv2的方法。

先介绍一点基础知识：

（1）常用的匹配算法有两种，一种是FlannBasedMatcher另外一种是 BFMatcher

     二者的区别在于BFMatcher总是尝试所有可能的匹配，从而使得它总能够找到最佳匹配，
    这也是Brute Force（暴力法）的原始含义。而FlannBasedMatcher中FLANN的含义是
    Fast Library forApproximate Nearest Neighbors，从字面意思可知它是一种近似法，
    算法更快但是找到的是最近邻近似匹配，所以当我们需要找到一个相对好的匹配但是不需要
    最佳匹配的时候往往使用FlannBasedMatcher。当然也可以通过调整FlannBasedMatcher的
    参数来提高匹配的精度或者提高算法速度，但是相应地算法速度或者算法精度会受到影响。

（2）.match与.knnMatch的匹配结果分别存储在vector以及vector >中

.match保存与特征点距离最近的一个，而knnMatch里边的vector存储与原图像特征点最接近的k个特征点

（3）DMatch数据结构包含三个非常重要的数据分别是queryIdx，trainIdx，distance
       queryIdx：测试图像的特征点描述符的下标（第几个特征点描述符），同时也是描述符对应特征点的下标。
       trainIdx：样本图像的特征点描述符下标, 同时也是描述符对应特征点的下标。
       distance：代表这怡翠匹配的特征点描述符的欧式距离，数值越小也就说明俩个特征点越相近。

（4）每个特征点本身具有以下属性：.pt:关键点坐标，.angle：表示关键点方向，.response表示响应强度，.size:标书该点的直径大小。

测试图像左边为image1、右边是image2均来源于链接11，如有侵权，联系笔者删除。

    

测试代码：

#include "highgui/highgui.hpp"    
#include "opencv2/nonfree/nonfree.hpp"    
#include "opencv2/legacy/legacy.hpp"   
#include   
using namespace cv;
using namespace std;

int main()
{

	Mat image01 = imread("image1.jpg", 1);
	Mat image02 = imread("image2.jpg", 1);
	
	//灰度图转换  
	Mat image1, image2;
	cvtColor(image01, image1, CV_RGB2GRAY);
	cvtColor(image02, image2, CV_RGB2GRAY);

	//计算特征点及描述子的方法1
	提取特征点    
	//SiftFeatureDetector siftDetector;  //定义sift特征点提取器，siftDetector后边可以加括号，里头放置参数，但我没找到函数原型，先这么用吧
	//vector keyPoint1, keyPoint2;

	检测特征点
	//siftDetector.detect(image1, keyPoint1);
	//siftDetector.detect(image2, keyPoint2);

	绘制特征点
	//Mat feature_pic1, feature_pic2;
	//drawKeypoints(image01, keyPoint1, feature_pic1, Scalar(0, 0, 255));//第一个参数是原始图像、第二个参数是特征点的向量、第三个参数是生成图像、第四个是颜色、是否绘制方向
	//drawKeypoints(image02, keyPoint2, feature_pic2, Scalar::all(-1), DrawMatchesFlags::DRAW_RICH_KEYPOINTS);//颜色随机带有方向
	//imshow("feature_pic1", feature_pic1);
	//imshow("feature_pic2", feature_pic2);
	特征点描述，为下边的特征点匹配做准备    
	//SiftDescriptorExtractor SiftDescriptor;//定义sift描述子提取器
	//Mat imageDesc1, imageDesc2;
	分别计算特征点对应的描述子
	//SiftDescriptor.compute(image1, keyPoint1, imageDesc1);
	//SiftDescriptor.compute(image2, keyPoint2, imageDesc2);

	//计算特征点及描述子的方法2
	vector keyPoint1, keyPoint2;
	Mat imageDesc1, imageDesc2;
	SIFT sift;
	sift(image1, Mat(), keyPoint1, imageDesc1);
	sift(image2, Mat(), keyPoint2, imageDesc2);
	Mat feature_pic1, feature_pic2;
	drawKeypoints(image01, keyPoint1, feature_pic1, Scalar(0, 0, 255));//第一个参数是原始图像、第二个参数是特征点的向量、第三个参数是生成图像、第四个是颜色、是否绘制方向
	drawKeypoints(image02, keyPoint2, feature_pic2, Scalar::all(-1), DrawMatchesFlags::DRAW_RICH_KEYPOINTS);//颜色随机带有方向
	imshow("feature_pic1", feature_pic1);
	imshow("feature_pic2", feature_pic2);
	
	//1.Flannbasedmatcher+knnMatch+Lowe's algorithm筛选
	FlannBasedMatcher flannmatcher;
	vector > matchePoints;
	vector GoodMatchePoints;
	flannmatcher.knnMatch(imageDesc1, imageDesc2, matchePoints, 2);
	cout << "total match points: " << matchePoints.size() << endl;
	// Lowe's algorithm,获取优秀匹配点  knn的两个邻近点的距离比值小于一个比例
	for (int i = 0; i < matchePoints.size(); i++)
	{
		if (matchePoints[i][0].distance < 0.6 * matchePoints[i][1].distance)
		{
			GoodMatchePoints.push_back(matchePoints[i][0]);
		}
	}

	Mat SIFT_match_flann;
	//绘制匹配
	drawMatches(image01, keyPoint1, image02, keyPoint2, GoodMatchePoints, SIFT_match_flann);
	imshow("SIFT_match_flann ", SIFT_match_flann);

	//2.BFMatcher+knnMatch+Lowe's algorithm筛选
	BFMatcher bfmatcher;
	vector > matchePoints1;
	vector GoodMatchePoints1;
	bfmatcher.knnMatch(imageDesc1,imageDesc2, matchePoints1, 2);
	cout << "total match points: " << matchePoints1.size() << endl;
	for (int i = 0; i < matchePoints1.size(); i++)
	{
		if (matchePoints1[i][0].distance < 0.6 * matchePoints1[i][1].distance)
		{
			GoodMatchePoints1.push_back(matchePoints1[i][0]);
		}
	}
	Mat SIFT_match_bf;
	//绘制匹配
	drawMatches(image01, keyPoint1, image02, keyPoint2, GoodMatchePoints1, SIFT_match_bf);
	imshow("SIFT_match_bf ", SIFT_match_bf);

	3.BFMatcher+matcher+nth_element
	BFMatcher bfmatcher_nth;
	vector MatchePoints2;
	bfmatcher_nth.match(imageDesc1, imageDesc2, MatchePoints2);
	nth_element(MatchePoints2.begin(), MatchePoints2.begin() + 29, MatchePoints2.end());   //提取出前30个最佳匹配结果     
	MatchePoints2.erase(MatchePoints2.begin() + 30, MatchePoints2.end());    //剔除掉其余的匹配结果

	Mat SIFT_match_bf_nth;
	drawMatches(image01, keyPoint1, image02, keyPoint2, MatchePoints2, SIFT_match_bf_nth, Scalar(0, 255, 0), Scalar::all(-1));//匹配特征点绿色，单一特征点颜色随机
	imshow("SIFT_match_bf_nth ", SIFT_match_bf_nth);


	//4.BFMatcher+matcher+按最小距离的两倍筛选
	BFMatcher bfmatcher_less_twomindis;
	vector MatchePoints3;
	bfmatcher_less_twomindis.match(imageDesc1, imageDesc2, MatchePoints3);

	double max_dist = MatchePoints3[0].distance, min_dist = MatchePoints3[0].distance;
	for (int i = 1; i max_dist)
			max_dist = MatchePoints3[i].distance;
		if (MatchePoints3.at(i).distance < min_dist)
			min_dist = MatchePoints3[i].distance;
	}
	cout << "min_distance=" << min_dist << endl;
	cout << "max_distance=" << max_dist << endl;

	//匹配结果删选    
	vectorgood_matches_less_twomindis;
	for (int i = 0; i

上面的方法均可以组合使用。

代码结果：

3.SURF（Speeded Up Robust Features，加速稳健特征）

3.1与SIFT的关系

        SURF算法是对SIFT算法的改进，主要是速度方面的改进。实验证明，SURF算法较SIFT在运算速度上要快3倍左右。SURF在执行效率上有两大制胜法宝——一个是积分图在Hessian（黑塞矩阵）上的使用，一个是降维的特征描述子的使用。

3.2SIFT特征提取和匹配过程

输入图像-》图像灰度化-》构建尺度空间-》空间极值点检测-》稳定关键点的定位-》稳定关键点方向信息分配-》关键点描述-》特征点匹配

在介绍过程前先介绍些预备知识：（1）积分图  （2）Hessian矩阵及在SURF中应用

（1）积分图 

        积分图是数字图像处理中常用的一种方法，通常能够很大程度的加速计算过程。对于一幅灰度图像，积分图像中的任意一点(x,y)的值是指从图像的左上角到这个点的所构成的矩形区域内所有的点的灰度值之和。该部分内容可以看一位大佬知乎上写的数字图像处理之积分图 - 知乎 (zhihu.com)，描述的很清楚。

（2）Hessian矩阵及在SURF中应用

定义：

黑塞矩阵（Hessian Matrix）是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。

对一个图像f(x,y)，其Hessian矩阵如下：

当Hessian矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或更暗的点，由此来定位关键点的位置。

Hessian矩阵的判别式为：

可以看到，Hessian矩阵的判别式，其实就是当前点对水平方向二阶偏导乘以垂直方向的二阶偏导再减去当前点水平、垂直二阶偏导的二次方。

在SURF算法中的应用：

在SURF算法中，因为特征点需要具备尺度无关性，所以在构造Hessian矩阵构造前，需要对其进行高斯滤波，为便于使用积分图加速，计算SURF使用了盒式滤波器来近似替代高斯滤波器。盒式滤波器（Boxfilter）对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题。

加上盒式滤波之后的每个像素的Hessian矩阵行列式的近似值（Dxx、Dxy和Dyy表示模板与图像进行卷积的结果）：

在Dxy上乘了一个加权系数0.9，目的是为了平衡因使用盒式滤波器近似所带来的误差。

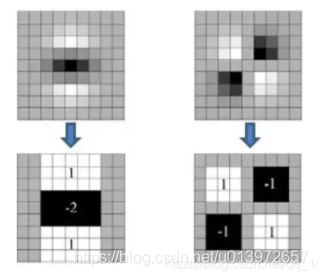
下面展示高斯滤波器和盒式滤波器在图像上二阶导数的示意图（该图源于链接13，为便于理解放于此处，如有侵权联系笔者删除）：

上边两幅图是9*9高斯滤波器模板分别在图像上垂直方向上二阶导数Dyy和Dxy对应的值，下边两幅图是使用盒式滤波器对其近似，灰色部分的像素值为0，黑色为-2，白色为1。

使用近似的Hessian矩阵行列式来表示图像中某一点x处的斑点响应值，遍历图像中所有的像元点，便形成了在某一尺度下关键点检测的响应图像。使用不同的模板尺寸，便形成了多尺度斑点响应的金字塔图像。

流程中每一步与SIFT对比：

1.构建尺度空间：SURF构造的金字塔图像与SIFT很大不同，SIFT采用的是DOG图像，而SURF采用的是Hessian矩阵行列式近似值图像。 在SIFT金字塔中不同的组间会采用下采样，而SURF不需要，它通过调节盒状滤波器的大小来构建尺度金字塔。盒式滤波器（Boxfilter）将图像的滤波转化成计算图像上不同区域间像素和的加减运算问题，转换后便于使用积分图，可以加速。

2.极值点检测及稳定关键点定位：SURF算法通过Hessian矩阵来检测候选特征点，然后再对非极大值的点进行抑制。而且Hessian矩阵行列式的最大值在尺度和图像空间被插值。与SIFT基本一致邻域。当Hessian矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或更暗的点，由此来定位极值点的位置。

3.方向信息分配：SURF对图像使用Haar小波响应运算代替直接的梯度运算，使用haar主要是便于利用积分图像，提高图像梯度的计算效率。与SIFT一样，会给这些响应以兴趣点为中心使用高斯函数加权。求取主方向值，需要设计一个以特征点为中心，张角为60度的扇形滑动窗口，统计这个扇形区域内的haar小波特征总和。以步长为0.2弧度左右，旋转这个滑动窗口，再统计小波特征总和。小波特征总和最大的方向为主方向。特征总和的求法是对图像Harr小波响应值dx、dy进行累加，得到一个矢量（）:

主方向为最大Harr响应累加值所对应的方向，也就是最长矢量所对应的方向，即

  或者max{}

4.关键点描述：Surf算法中，也是在特征点周围取一个4*4的矩形区域块,但每个区域的边长为5，每个区域统计25个像素的水平方向和垂直方向的Haar小波特性（均相对于正方形框的主方向确定的），该haar小波特征为水平方向值之和、垂直方向值之和、水平方向绝对值之和以及垂直方向绝对值之和4个方向。如下图（该图源于链接13，为便于理解放于此处，如有侵权联系笔者删除）

把这4个值作为每个子块区域的特征向量，所以一共有4*4*4=64维向量作为SURF特征的描述子，比SIFT特征的描述子减少了一半。

3.3opencv SURF描述子的调用及计算

 opencv2与opencv3中SURF的使用方法是不同的，opencv3要使用SURF需要先cmake编译。此处展示opencv2的方法。

SIFT部分中介绍的方法都可以类似使用。

测试代码：

#include "highgui/highgui.hpp"    
#include "opencv2/nonfree/nonfree.hpp"    
#include "opencv2/legacy/legacy.hpp"   
#include   
using namespace cv;
using namespace std;
int main()
{
	Mat image01 = imread("image1.jpg", 1);
	Mat image02 = imread("image2.jpg", 1);

	//灰度图转换  
	Mat image1, image2;
	cvtColor(image01, image1, CV_RGB2GRAY);
	cvtColor(image02, image2, CV_RGB2GRAY);

	vector keyPoint1, keyPoint2;
	Mat imageDesc1, imageDesc2;
	SURF surf;
	surf(image1, Mat(), keyPoint1, imageDesc1);
	surf(image2, Mat(), keyPoint2, imageDesc2);

	BFMatcher bfmatcher_less_twomindis;
	vector MatchePoints3;
	bfmatcher_less_twomindis.match(imageDesc1, imageDesc2, MatchePoints3);

	double max_dist = MatchePoints3[0].distance, min_dist = MatchePoints3[0].distance;
	for (int i = 1; i max_dist)
			max_dist = MatchePoints3[i].distance;
		if (MatchePoints3.at(i).distance < min_dist)
			min_dist = MatchePoints3[i].distance;
	}
	cout << "min_distance=" << min_dist << endl;
	cout << "max_distance=" << max_dist << endl;

	//匹配结果删选    
	vectorgood_matches_less_twomindis;
	for (int i = 0; i

测试结果：

总体来说，SURF和SIFT算法在特征点的检测取得了相似的性能，SURF借助积分图，将模板卷积操作近似转换为加减运算，在计算速度方面要优于SIFT特征。

文中若有错误及不妥之处，还望指出！