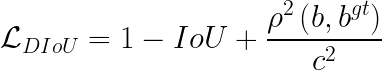目标检测中预测框回归优化IOU、GIOU、DIOU、CIOU、EIOU(二)
目录
IOU GIOU DIOU CIOU
IOU、GIOU、DIOU、CIOU 损失函数对比
EIOU计算和损失函数
总结
目标检测分为:目标分类 + 目标定位两个任务。
目标分类就是要对该目标进行分类以确定该目标属于什么类别以及其属于该类别的置信度。
目标定位是要在图像中确定目标的位置,输出其在图像中的坐标信息。目标定位依赖边界框回归模块去定位目标。边界框回归是指使用矩形边界框去预测目标对象在图像中的位置,然后不断细化预测边界框的位置。
不断细化预测的边界框的位置是通过定义边界框回归损失函数,计算回归损失值 Loss 然后进行反向梯度下降实现的。起初定义计算边界框回归的损失函数使用的是基于 L1、L2 距离范数。
- 基于 L1 范数定义的边界框损失函数指预测边界框的四个点
 坐标和真实边界框对应的四个点
坐标和真实边界框对应的四个点  横坐标和纵坐标分别计算绝对值之差然后相加。
横坐标和纵坐标分别计算绝对值之差然后相加。 - 基于 L2 范数定义的边界框损失函数是指预测边界框的四个点
 坐标和真实边界框对应的四个点
坐标和真实边界框对应的四个点  横坐标和纵坐标分别计算平方和之差然后相加。
横坐标和纵坐标分别计算平方和之差然后相加。
L1 范数:
L2 范数:
L1 范数和 L2 范数定义的边界框回归的损失函数 Loss 都是将预测的 bbox 和真实框 bbox 的四个点分别求 Loss 值然后相加,并没有考虑坐标之间的相关性。
如下图所示,绿色框为真实框,黑色框为预测的边界框。由图可知,预测框和真实框三种不同位置和不同区域的相交(暂时只关注 L1 范数、L2 范数),最终基于 L1 范数和 L2 范数定义的边界框回归损失函数在计算得到的边界框回归损失Loss值都是一样的。
但肉眼可以观察出,图 (a) 和图 (b) 中最后一种预测的框和真实框重合明显好于前面两种。而基于 L1 范数和 L2 范数定义的边界框回归损失函数计算得到边界框回归损失值是难以判别优劣。
这一点可以通过 IOU 定义的损失函数计算的损失值来区别,因此提出了基于交并比的 IOU 定义的边界框回归损失函数。
注意本文的用词: 完全重合(预测框和真实框大小一模一样)、部分重合(相交)、水平和垂直方向上的重合(闭包,预测框包含在真实框内部)、不相交(完全不重合)。
IOU
边界框回归损失函数(IoU_Loss),它是将边界框的4个点构成的 box 看成整体进行回归,其考虑到了坐标之间的相关性。
IoU 的全称为交并比(Intersection over Union),其计算是 “预测的边框” 和 “真实的边框” 的交集和并集的比值,IOU计算公式如下所示(IOU的值域为[ 0,1 ]):
IoU_Loss 本身是是从人脸检测的 paper 引入进来的(https://arxiv.org/pdf/1608.01471.pdf),如下图所示:
IOU回归损失Loss算法计算流程
其中, ![]() 是预测边界框(Bounding box)的面积,
是预测边界框(Bounding box)的面积,![]() 是真实边界框(Bounding box)的面积,
是真实边界框(Bounding box)的面积, ![]() 是两个区域的交集,
是两个区域的交集,![]() 是两个区域的并集。
是两个区域的并集。![]() 是对 IOU 的交叉熵损失函数,
是对 IOU 的交叉熵损失函数,![]() 是对 IOU 取负对数。
是对 IOU 取负对数。
在实际使用中,实际很多 IoU 的损失 Loss 常常被定义为Loss(IoU) = 1-IoU。它们完全重合时,IoU 就是 1,那么对于 Loss 来说,Loss是越小越好,说明他们重合度高,所以 IoU_Loss 就可以简单表示为 1- IoU。
边界框 box 位置的修正是通过对 IOU 的损失函数的损失值loss进行反向传播迭代计算的。
IOU回归的优缺点
-
1、当预测框和真实框完全不相交时,IOU=0,如下图状态 1。此时损失函数 -ln(IOU)不可导,因此 IoU_Loss 无法优化两个框不相交的情况。这时的 IOU 不能反映真实框和预测的边界框距离的远近。也因为不可导,所以没有梯度回传,无法进行下一步训练。
-
2、预测框和真实框无法反映相交程度的大小和好坏。如下图的状态 2 和状态 3,这两种预测框和真实框重合的情况下,两者的 IOU 值相同,IOU不能反映两个框是如何相交的。
-
3、IOU_Loss 解决了 L1 和 L2 范数定义的边界框回归损失函数的系列变量(边界框的四个点)相互独立和不具有尺度不变性的两大问题。相互独立是指 L1 范数和 L2 范数定义的损失函数:先独立地求出 4 个点的损失 Loss,然后进行相加,这种做法假设了边界框的4个点是相互独立的,但实际上应该是有一定相关性的,因为边界框的 4 个点都依赖于同一个目标。尺度不变性则指基于 L1 范数和 L2 范数的大边界框的 L2 损失通常会大于小边界框的损失,这使得在网络训练过程中,网络会更加注重大边界框的定位,忽视小边界框的定位,最终导致模型对小目标的检测性能比较差。
GIOU
GIOU 的诞生是为了解决 IOU 定义的损失函数无法优化预测框和真实框不相交的情况,以及不知道预测框和真实框如何相交的两个问题。
斯坦福学者在2019年的文章《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》中提出了 GIOU_Loss,在 IOU 的基础上引入了预测框和真实框的最小外接矩形。
GIOU定义及边界框回归损失函数:
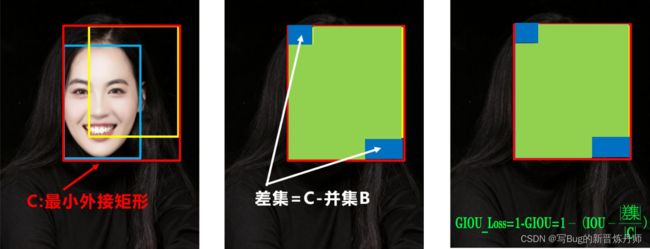
如下图,蓝色为真实框,黄色为预测的边界框,则 GIOU 计算公式如下:
其中红色闭包框C为能包含预测框和真实框最小的外接矩形框。从计算公式可以看出 GIOU 不仅关注重叠区域,还关注其他的非重合区域,可以更好的反映预测框和真实框的重合度。
GIoU 和 IoU 一样可以作为损失函数,Loss(GIoU) = 1 - GIoU。IOU的值域为 [0,1],而 GIoU 有对称区间,取值范围 [-1,1]。
GIOU 边界框回归的优缺点
-
1、GIoU 能够更好地反映预测框和真实框相交的情况,如下图所示,虽然两种情况下计算得到的 IOU 一致,但是 (a) 中两个框相交的更为整齐,因此 (a) GIOU 要比(b)中大。GIoU 考虑到了 IoU 没有考虑到的预测框和真实框的非重叠区域,能够反映出真实框 A、预测框 B 重叠的方式。
-
2、当预测框和真实框不重合时,不重合度越高 GIOU 的值越接近于-1,此时的GIOU等于(IOU = 0)
,最大化 GIOU 就是指使得预测框和真实框不断地靠近,以此达到回归优化边界框的目的。
- 3、当预测框和真实框完全重合时(预测框在真实框的内部),IoU 和 GIoU的 损失值 Loss 都一样时,此时的 GIoU 退化为 IoU,GIOU=IOU,无法区分预测框和真实框的位置关系,也导致此时的边界框回归收敛很慢。
DIOU
基于 GIoU 的缺点(GIoU 退化为 IoU的情况),因此提出 DIoU,其论文为:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression。
DIOU计算公式及回归损失函数:
其中 d(Distance_2)表示预测框与真实框中心点的欧式距离,c(Distance_C)表示覆盖预测框与真实框的最小闭合框的对角线长度。
上图中蓝色框为真实框,黄色框为预测框,红色框为能包含预测框和真实框的最小外界矩形框。
与 IOU、GIoU 定义损失函数类似,Loss(DIOU)= 1-DIOU,计算公式如下所示:
![]() 分别代表真实框和预测框的中心点,
分别代表真实框和预测框的中心点,![]() 代表的是计算预测框和边界框两中心点间的欧式距离(Distance_C),
代表的是计算预测框和边界框两中心点间的欧式距离(Distance_C),![]() 表示预测框和边界框中心点的间的欧式距离的平方(Distance_2)。当预测框和真实框完全重合时,L(GIOU)=L(GIOU)=L(DIOU)=0;完全重叠是指预测框和真实框大小一模一样。
表示预测框和边界框中心点的间的欧式距离的平方(Distance_2)。当预测框和真实框完全重合时,L(GIOU)=L(GIOU)=L(DIOU)=0;完全重叠是指预测框和真实框大小一模一样。
DIOU边界框回归的优缺点
-
2、DIoU loss 通过最小化预测框和真实框中心点的距离来进行收敛,而GIOU loss优化的是预测框和真实框之间的面积(减少外界包围框的面积)来进行收敛,因此DIOU loss 比GIoU loss回归收敛要快得多。即使预测框和真实框在水平和垂直两个方向上同时重合时(即预测框在真实框内部的时候),也可以通过最小化中心点的距离,来继续进行水平方向和垂直方向的预测框回归,而此时这种情况下的GIOU=IOU,GIOU损失退化为了IOU损失,基本上很难收敛。
-
3、DIoU可以替换普通的IoU评价策略,应用于NMS,使得NMS得到的结果更加合理、有效。
CIOU
虽然DIOU解决了当预测框和真实框相交(部分重叠)、预测框包含在真实框内部两种情况下的预测框回归收敛问题,但是这都是通过最小化预测框和真实框两个中心点的距离实现的。为了加快这两种情况下的预测框回归收敛更快、更准确,因此提出了CIOU。
CIOU 计算公式
一个好的目标框回归损失应该考虑三个重要的几何因素:重叠面积、中心点距离、长宽比。
预测框和目标框之间的长宽比的一致性是极其重要的,因此 CIOU 在 DIOU 的基础上添加了一个边界框 box 长宽比的惩罚项,CIOU 的损失函数计算公式如下:
CIOU 边界框损失函数
CIOU 和 IOU、GIOU、CIOU 损失函数设置一样,CIOU 的损失函数为 Loss(CIOU)=1-CIOU
其中 α 是用于平衡比例的参数,v 用来衡量预测框和真实框的宽和高之间的比例一致性。b代表预测框,![]() 代表真实框,
代表真实框,![]() 代表真实框的宽和高,w 和 h代表预测框的宽和高。
代表真实框的宽和高,w 和 h代表预测框的宽和高。
CIOU边界框回归的优点
-
从CIOU边界框损失函数可以看出,它包含了预测框和真实框重叠区域面积的 IOU 损失、预测框和真实框中心点之间归一化后的距离损失、预测框和真实框的宽和高的纵横比损失三个部分。CIOU边界框损失函数通过迭代可以将预测框不断向真实框移动,还尽可能的保证了预测框和真实框的宽和高的纵横比更为接近,加快了预测框的回归收敛速度。
CIOU边界框回归的缺点
CIOU Loss虽然考虑了边界框回归:预测框和真实框重叠面积、预测框和真实框的中心点距离、预测框和真实框高和宽的纵横比三个方面。
但从公式可以看出 CIoU 使用的是预测框和真实框的宽和高的相对比例,并不是宽和高的值。根据 纵横比 v 的定义,可以看出只要预测框的宽和高和真实框的比例满足:
![]()
那么 CIoU 中的添加的相对比例的惩罚项便不再起作用。从预测框的宽和高的相对于 v 的公式:
可以推导出:
表明预测框 w 和 h 的梯度值 ![]() 和
和 ![]() 是具有相反的符号。这个相反的符号在训练的过程中问题就很大,它表明预测框回归过程中 w 和 h 其中某一个值增大时,另外一个值必须减小,预测框回归过程中它的 w 和 h 不能同增或者同减。
是具有相反的符号。这个相反的符号在训练的过程中问题就很大,它表明预测框回归过程中 w 和 h 其中某一个值增大时,另外一个值必须减小,预测框回归过程中它的 w 和 h 不能同增或者同减。
CIOU总结:CIOU 将边界框的纵横比作为惩罚项加入到边界框损失函数中,一定程度上可以加快预测框的回归收敛过程,但是一旦收敛到预测框和真实框的宽和高呈现线行比例时,就会导致预测框回归时的宽和高不能同时增大或者减少。
IOU、GIOU、DIOU、CIOU 损失函数对比
下图显示了几种IoU损失函数在不同迭代次数情况下的回归误差曲线:
-
由于IoU损失只有在预测框与真实框有重叠的情况下才有效,因此收敛得很慢,得到的预测框与真实框之间的误差也很大;
-
GIoU损失通过增加预测框的大小慢慢移动到与真实框重叠的区域来帮助处理非重叠的情况,其迭代过程收敛得比较缓慢,尤其是预测框与真实框的纵横比相差很大的时候,这种情况下GIoU回归得到的预测框与真实框之间的误差也比较大。
-
DIoU 和 CIoU损失可以收敛得比IoU和GIoU更快,特别是CIoU收敛速度和回归的精度都比使用它之前几种损失函数得到的结果更好。
下图是在 YOLOv3 上几种边界框回归损失函数对模型提升效果对比图
总结
-
IOU 解决了 L1、L2 初步预测框和真实框三种不同位置和不同区域的相交时的判断,但是没有解决预测框和真实框无法反映相交程度的大小和好坏。当预测框在真实框内部时的不同位置时,IOU 是一样的,无法继续优化。预测框和真实框不相交时,IOU=0,也没有办法继续进行优化。
-
GIOU 通过预测框和真实框的最小外接闭包矩形解决了IOU,当预测框和真实框不相交时无法继续优化问题,但是没有解决当预测框在真实框内部不同位置时的优化问题。
-
DIOU 通过直接优化预测框和真实框两个中心点的距离和两个框的最小外接矩形对角线的距离解决了 GIOU,当预测框在真实框内部不同位置时的回归收敛问题。
-
CIOU 通过在 DIOU 的基础上添加了预测框和真实框的宽高纵横比的惩罚项,加快了预测框和真实框回归收敛的速度。
EIOU计算和损失函数
CIOU 损失,在DIOU损失的基础上添加了衡量预测框和真实框纵横比 v,在一定程度上可以加快预测框的回归速度,但是存在的问题是预测框回归过程中,一旦预测框和真实框的宽高纵横比呈现线性比例时,预测框 w 和 h 不能同时增加或者减少,就不能继续进行回归优化了。
2021 年中科院提出了 EIOU,论文:《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》, EIOU 是在 CIOU 的惩罚项基础上将预测框和真实框的纵横比的影响因子拆开,分别计算预测框和真实框的长和宽,来解决 CIOU 存在的问题。
EIOU回归损失函数
CIOU 回归损失 Loss(CIOU):
EIOU 回归损失 Loss(EIOU):
其中 Cw 和 Ch 是覆盖预测框真实框的最小外接框的宽度和高度。
从 EIOU 损失函数公式可以看出,EIOU 损失函数包含三个部分:预测框和真实框的重叠损失LIou,预测框和真实框的中心距离损失Ldis,预测框和真实框的宽和高损失Lasp。EIOU 损失的前两部分延续 CIOU 中的方法,但是宽高损失直接使预测框与真实框的宽度和高度之差最小,使得收敛速度更快。
下图是 CIOU 和 EIOU 损失预测框的迭代过程对比图,红色框和绿色框就是预测框的回归过程,蓝色框是真实框,黑色框是预先设定的锚框,可以看出 CIOU 的问题是宽和高不能同时增大或者减少,而 EIOU 可以。
EIOU回归损失的优点
-
将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值,加速了预测框的收敛、提高了预测框的回归精度。
此外在这篇论文《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》中引入的Focal-EIoU Loss,是指对EIOU损失(Loss(EIOU)中进行加权处理。
![]()
其中,γ 为控制异常值抑制程度的参数。
Focal-EIoU Loss 与传统的 Focal Loss 有一定的区别,传统的Focal Loss针对越困难的样本损失越大,起到的是困难样本挖掘的作用;而Focal-EIoU Loss:和真实框IOU越高的,预测框的损失越大。这就相当于加权作用,给越好的回归目标一个越大的损失,有助于提高预测框的回归精度。
因为在目标检测中,大部分最开始根据预先设定的锚框得到的预测框都和ground truth(真实框)的IoU不大,这一部分叫做低质量样本,而在低质量样本上的训练容易造成损失值的剧烈波动。而Focal-EIoU Loss的提出目标便是解决高低质量样本类别不平衡的问题,也就是说减少与真实框重叠较少的大量预先设定的锚框而得到的预测框的损失值,减少其对预测框回归优化过程中的贡献,使预测框回归过程专注于高质量锚框(即和真实框IOU比较大的预先设定的锚框得到的预测框)。
Focal loss是最初由何恺明提出的,最初用于图像领域解决数据不平衡造成的模型性能问题。传统Focal Loss计算公式如下:
但是 EIOU 的论文作者尝试直接将 EIOU 代替,发现不太好,就改成了 Focal-EIoU Loss:LEIOU的形式,也就是最终论文中出现的 Focal-EIoU Loss。
总结
预测框回归的三大几何因素:预测框和真实框的重叠面积、预测框和真实框的中心点距离、预测框和真实框的宽和高的纵横比(宽和高的比例、还要考虑宽和高的差异)。
-
IOU Loss:考虑了重叠面积,归一化坐标尺度;
-
GIOU Loss:考虑了重叠面积,基于IOU解决边界框不相交时loss等于0的问题;
-
DIOU Loss:考虑了重叠面积和中心点距离,基于IOU解决GIOU收敛慢的问题;
-
CIOU Loss:考虑了重叠面积、中心点距离、纵横比,基于DIOU提升回归精确度;
-
EIOU Loss:考虑了重叠面积,中心点距离、长宽边长真实差,基于CIOU解决了纵横比的模糊定义,并添加Focal Loss解决预测框回归中的样本不平衡问题。
参考链接:
目标检测中的预测框回归优化之IOU、GIOU、DIOU、CIOU和EIOU (qq.com)
深入浅出Yolo系列之Yolov3&Yolov4&Yolov5&Yolox核心基础知识完整讲解 - 知乎 (zhihu.com)