聚类算法Kmens和密度峰值聚类

目录

Kmeans算法

原理

改进

代码

效果 

密度峰值算法

原理

代码

效果 

---

Kmeans算法

原理

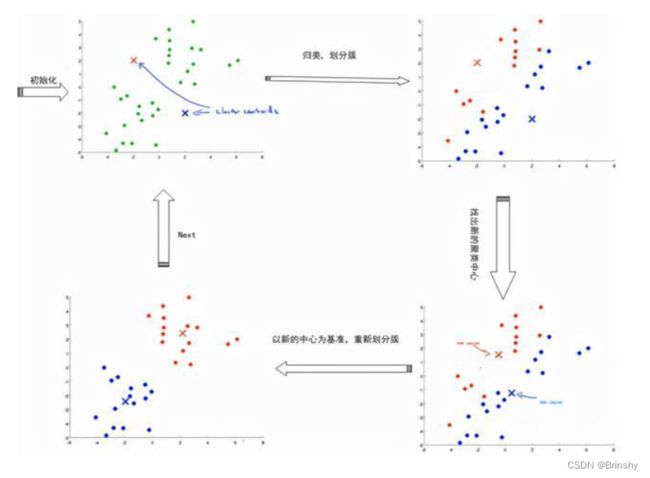
kmeans算法的原理是不断地迭代聚类中心点，主要步骤如下：

(1) 从 n个数据对象任意选择 k 个对象作为初始聚类中心;

(2) 根据每个聚类对象的均值(中心对象)，计算每个对象与这些中心对象的距离;并根据最小距离重新对相应对象进行划分;

(3) 重新计算每个(有变化)聚类的均值(中心对象);

(4) 计算标准测度函数，当满足一定条件，如函数收敛时，则算法终止;如果条件不满足则回到步骤(2)。

图片源地址「Python机器学习实战」聚类算法（1）——K-Means聚类|数据点|kmeans_网易订阅

改进

对于数据的处理我们可以利用pca以及熵权法进行一定的降维和权重的改变，使得部分不太合理的数据维数，变得权重更小，部分重要的数据权重变大。从而改善我们的聚类质量。

而利用kmeans++可以使得初始选点更加合理，减少因为初始点位不合引起的聚类暴毙。

其中利用的方法有：

        熵权法

        PCA降维

        利用Kmeans++

代码

from numpy import *
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np
import time
import itertools

INF = 999999999.0

def assess_clustering(list1, list2):
    a = b = c = d = 0
    for j in range(len(list1)):
        if list1[j][0] == list1[j][1] and list2[j][0] == list2[j][1]:
            a = a + 1
        elif list1[j][0] == list1[j][1] and list2[j][0] != list2[j][1]:
            b = b + 1
        elif list1[j][0] != list1[j][1] and list2[j][0] == list2[j][1]:
            c = c + 1
        else:
            d = d + 1
    jc = a / (a + b + c)
    fmi = sqrt(a / (a + b) * a / (a + c))
    Rand = (a + d) / len(list1)
    return jc, fmi, Rand


def loadDataSet(fileName, splitChar='\t'):
    """
    输入：文件名
    输出：数据集
    描述：从文件读入数据集
    """
    dataSet = []
    ori_labels = []
    with open(fileName) as fr:
        for line in fr.readlines():
            curline = line.strip().split(splitChar)
            ori_labels.append(curline.pop(-1))
            fltline = list(map(float, curline))
            dataSet.append(fltline)
    return dataSet, ori_labels

# 归一化
def Normalization(dataSet, W=[1] * 666):
    row = shape(dataSet)[0]
    col = shape(dataSet)[1]
    sum = 0
    mean, si = [], []

    for j in range(col):
        for i in range(row):
            sum += dataSet[i][j]
        mean.append(sum / row)
        sum = 0

    for j in range(col):
        for i in range(row):
            sum += (dataSet[i][j] - mean[j]) ** 2
        si.append(sqrt(sum / row))
        sum = 0

    for j in range(col):
        for i in range(row):
            dataSet[i][j] = (dataSet[i][j] - mean[j]) / si[j] * W[j]
    return dataSet


def PCA_function(dataSet):
    pca = PCA(n_components=2)
    pca.fit(np.array(dataSet))
    new_dataSet = pca.transform(np.array(dataSet))
    k1_spss = pca.components_.T
    weight = (np.dot(k1_spss, pca.explained_variance_ratio_)) / np.sum(pca.explained_variance_ratio_)
    weighted_weight = weight / np.sum(weight)

    return list(new_dataSet), list(weighted_weight)


# 熵权法
def entropy(data0):
    # 返回每个样本的指数
    # 样本数，指标个数
    n, m = np.shape(data0)
    # 一行一个样本，一列一个指标
    # 下面是归一化
    maxium = np.max(data0, axis=0)
    minium = np.min(data0, axis=0)
    data = (data0 - minium) * 1.0 / (maxium - minium)
    ##计算第j项指标，第i个样本占该指标的比重
    sumzb = np.sum(data, axis=0)
    data = data / sumzb
    # 对ln0处理
    a = data * 1.0
    a[np.where(data == 0)] = 0.0001
    #    #计算每个指标的熵
    e = (-1.0 / np.log(n)) * np.sum(data * np.log(a), axis=0)
    #    #计算权重
    w = (1 - e) / np.sum(1 - e)
    return w  # sha##熵权法


def createDataSet():
    """
    输出：数据集
    描述：生成数据集
    """
    dataSet = [[0, 0], [0, 1], [0, 2], [0, 3], [0, 4],
                   [0, -1], [0, -2], [0, -3], [0, -4],
                   [1, 0], [2, 0], [3, 0], [4, 0],
                   [-1, 0], [-2, 0], [-3, 0], [-4, 0]]
    return dataSet


def distEclud(vecA, vecB):
    """
    输入：向量A, 向量B
    输出：两个向量的欧式距离
    """
    return sqrt(sum(power(vecA - vecB, 2)))


def randCent(dataSet, k):
    """
    输入：数据集, 聚类个数
    输出：k个随机质心的矩阵
    """
    n = shape(dataSet)[1]
    centroids = mat(zeros((k, n)))
    for j in range(n):
        minJ = min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ)
        centroids[:, j] = minJ + rangeJ * random.rand(k, 1)
    return centroids


def nearest(point, cluster_centers):
    '''
    计算point和cluster_centers之间的最小距离
    :param point: 当前的样本点
    :param cluster_centers: 当前已经初始化的聚类中心
    :return: 返回point与当前聚类中心的最短距离
    '''
    min_dist = INF
    m = np.shape(cluster_centers)[0]  # 当前已经初始化聚类中心的个数
    for i in range(m):
        # 计算point与每个聚类中心之间的距离
        d = distEclud(point, cluster_centers[i,])
        # 选择最短距离
        if min_dist > d:
            min_dist = d
    return min_dist


def loss(dataSet, clusterAssment, k):
    dataSet = mat(dataSet)
    num_inside = 0
    num_outside = 0
    temp = 0
    data = []
    for i in range(k):
        data.append(dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :])
    for i in range(len(data)):
        for j in range(len(data[i])):
            for k in range(len(data[i])):
                temp += distEclud(data[i][j], data[i][k]) ** 2
        num_inside += temp
        temp = 0

    for i in range(len(data)):
        for j in range(i + 1, len(data)):
            for k in range(len(data[i])):
                for l in range(len(data[j])):
                    temp += distEclud(data[i][k], data[j][l])**2
        num_outside += temp
        temp = 0
    return [num_inside, num_outside]


def get_cent(points, k):
    '''
    kmeans++的初始化聚类中心的方法
    :param points: 样本
    :param k: 聚类中心的个数
    :return: 初始化后的聚类中心
    '''
    m, n = np.shape(points)
    cluster_centers = np.mat(np.zeros((k, n)))

    # 1、随机选择一个样本点作为第一个聚类中心
    index = np.random.randint(0, m)
    cluster_centers[0,] = np.copy(points[index,])  # 复制函数，修改cluster_centers，不会影响points

    # 2、初始化一个距离序列
    d = [0.0 for _ in range(m)]

    for i in range(1, k):
        sum_all = 0
        for j in range(m):
            # 3、对每一个样本找到最近的聚类中心点
            d[j] = nearest(points[j,], cluster_centers[0:i, ])
            # 4、将所有的最短距离相加
            sum_all += d[j]
        # 5、取得sum_all之间的随机值
        sum_all *= random.rand()
        # 6、获得距离最远的样本点作为聚类中心点
        for j, di in enumerate(d):  # enumerate()函数用于将一个可遍历的数据对象（如列表、元组或字符串）组合为一个索引序列，同事列出数据和数据下标一般用在for循环中
            sum_all -= di
            if sum_all > 0:
                continue
            cluster_centers[i] = np.copy(points[j,])
            break
    return cluster_centers


def kMeans(dataSet, k, distMeans=distEclud, createCent=randCent):
    """
    输入：数据集, 聚类个数, 距离计算函数, 生成随机质心函数
    输出：质心矩阵, 簇分配和距离矩阵
    """
    m = shape(dataSet)[0]
    loss_data = [[]]+[[]]
    clusterAssment = mat(zeros((m, 2)))
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):  # 寻找最近的质心
            minDist = INF
            minIndex = -1
            for j in range(k):  # 从k个质心中找出最近的
                distJI = distMeans(centroids[j, :], dataSet[i, :])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i, 0] != minIndex:
                clusterChanged = True
            clusterAssment[i, :] = minIndex, minDist ** 2
        for cent in range(k):  # 更新第k个质心的位置
            ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]]
            centroids[cent, :] = mean(ptsInClust, axis=0)
        loss_r = loss(dataSet, clusterAssment, k)
        loss_data[0].append(loss_r[0])
        loss_data[1].append(loss_r[1])
    return centroids, clusterAssment, loss_data


def plotFeature(dataSet, centroids, clusterAssment, loss_data):
    m = shape(centroids)[0]
    fig = plt.figure()
    scatterMarkers = ['s', 'o', '^', '8', 'p', 'd', 'v', 'h', '>', '<']
    scatterColors = ['blue', 'green', 'yellow', 'purple', 'orange', 'black', 'brown']

    ax = fig.add_subplot(221)
    for i in range(m):
        ptsInCurCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :]
        markerStyle = scatterMarkers[i % len(scatterMarkers)]
        colorSytle = scatterColors[i % len(scatterColors)]
        ax.scatter(ptsInCurCluster[:, 0].flatten().A[0], ptsInCurCluster[:, 1].flatten().A[0], marker=markerStyle,
                   c=colorSytle, s=90)
    ax.scatter(centroids[:, 0].flatten().A[0], centroids[:, 1].flatten().A[0], marker='*', c='red', s=100)


    # bx = fig.add_subplot(111)
    # for i in range(1, 51):
    #     markerStyle = scatterMarkers[int(clusterAssment.A[i-1][0]) % len(scatterMarkers)]
    #     colorSytle = scatterColors[int(clusterAssment.A[i-1][0]) % len(scatterColors)]
    #     bx.scatter(i, 0, marker=markerStyle, c=colorSytle, s=3)
    # for i in range(51, 101):
    #     markerStyle = scatterMarkers[int(clusterAssment.A[i-1][0]) % len(scatterMarkers)]
    #     colorSytle = scatterColors[int(clusterAssment.A[i-1][0]) % len(scatterColors)]
    #     bx.scatter(i, 1, marker=markerStyle, c=colorSytle, s=3)
    # for i in range(101, 151):
    #     markerStyle = scatterMarkers[int(clusterAssment.A[i-1][0]) % len(scatterMarkers)]
    #     colorSytle = scatterColors[int(clusterAssment.A[i-1][0]) % len(scatterColors)]
    #     bx.scatter(i, 2, marker=markerStyle, c=colorSytle, s=3)

    #类内距离和类间距离
    cx = fig.add_subplot(222)
    x = range(1,len(loss_data[0])+1)
    cx.plot(x,loss_data[0])

    dx = fig.add_subplot(223)
    x = range(1, len(loss_data[1]) + 1)
    dx.plot(x, loss_data[1])

def main():
    dataSet, ori_labels = loadDataSet('聚类作业/data.txt', splitChar=',')
    #dataSet = createDataSet()
    W = list(entropy(dataSet))  # W为熵权法权重
    # dataSet, W = PCA_function(dataSet)#做pca降维，W为权重，第一个返回参数是降维后的数据集
    dataSet = Normalization(dataSet, W)  # 归一化
    dataSet = mat(dataSet)

    best_resultCentroids, best_clustAssing, best_loss_data = None, None, None
    best_JC, best_FMI, best_Rand, best_loss = 0, 0, 0, INF
    for k in range(1):
        resultCentroids, clustAssing, loss_data = kMeans(dataSet, 3, createCent=get_cent)  # createCent=get_cent

        #计算指标
        ans_labels = []
        for i in range(len(clustAssing.A)):
            ans_labels.append(clustAssing.A[i][0])
        comb1 = list(itertools.combinations(ori_labels, 2))
        comb2 = list(itertools.combinations(ans_labels, 2))
        JC, FMI, Rand = assess_clustering(comb1, comb2)

        if best_loss > loss_data[0][-1] / loss_data[1][-1]:
            best_resultCentroids, best_clustAssing, best_loss_data = resultCentroids, clustAssing, loss_data
            best_loss = loss_data[0][-1] / loss_data[1][-1]
            best_JC, best_FMI, best_Rand = JC, FMI, Rand

    plotFeature(dataSet, best_resultCentroids, best_clustAssing, best_loss_data)

    #聚类的指标参数
    print("JC", best_JC)
    print("FMI", best_FMI)
    print("Rand", best_Rand)

if __name__ == '__main__':
    start = time.perf_counter()
    main()
    end = time.perf_counter()
    print('finish all in %s' % str(end - start))
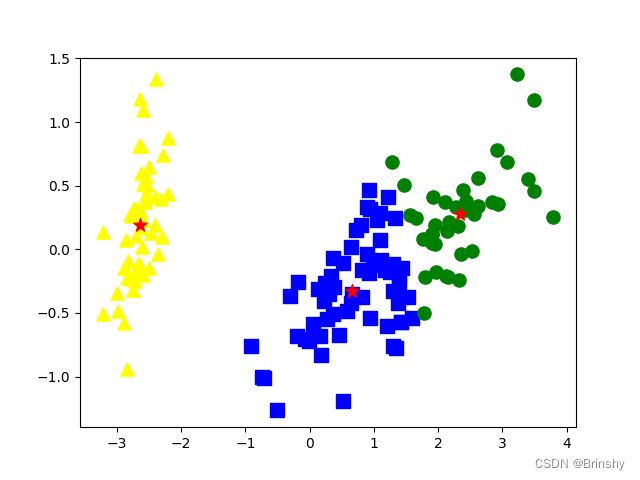
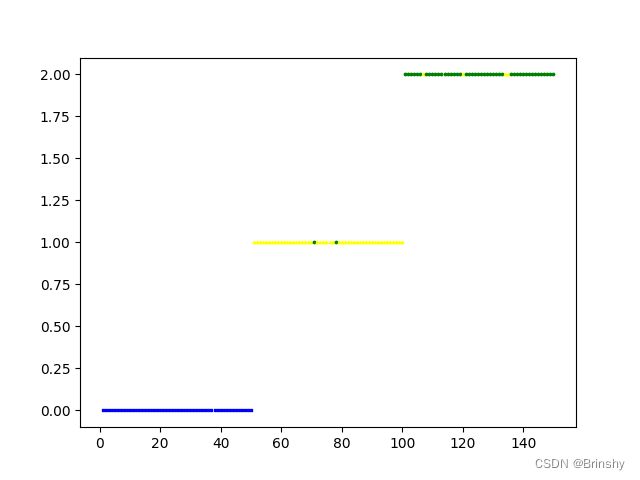
    plt.show()

效果 

密度峰值算法

原理

第1步，求每个点的密度rho。点的密度就是，以点为中心，以dc为半径，画一个小圆圈，数数里面几个点，圆圈中点的个数就是点的密度。（还可以用高斯核密度求点的密度，求出来的密度是连续型的）

第2步，计算每个点的delta。假设有一个点x，求比点x的密度大的且距离点x最近的那个点y，那么点x与点y之间的距离，就是点x的delta，就这样遍历所有点，把每个点的delta都求出来（注意，delta是距离，谁和谁的距离？x和y的距离，y是谁？y就是比x密度大，且距离x最近的那个点，要满足两个条件，密度比x大且距离最近）

第3步，每个点的密度rho和delta都求出来了，以rho为横坐标，delta为纵坐标，画个二维图，图中右上角的那几个点就是聚类中心，也就是rho和delta都很大的那几个点。（为什么？因为聚类中心有个特点，密度很大，且与密度比它大的点的距离也很大）

第4步，找到聚类中心了，就可以扩展聚类簇了，按照rho从大到小的顺序进行聚类扩展

图片地址为

百度安全验证

代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
from sklearn import metrics
import math
import itertools

UNCLASSIFIED = 0
NOISE = -1

# 计算数据点两两之间的距离
def getDistanceMatrix(datas):
    N,D = np.shape(datas)
    dists = np.zeros([N,N])
    
    for i in range(N):
        for j in range(N):
            vi = datas[i,:]
            vj = datas[j,:]
            dists[i,j]= np.sqrt(np.dot((vi-vj),(vi-vj)))
    return dists


#  寻找以点cluster_id 为中心，eps 为半径的圆内的所有点的id
def find_points_in_eps(point_id,eps,dists):
    index = (dists[point_id]<=eps)
    return np.where(index==True)[0].tolist()


# 聚类扩展
# dists ： 所有数据两两之间的距离  N x N
# labs :   所有数据的标签 labs N，
# cluster_id ： 一个簇的标号
# eps ： 密度评估半径
# seeds： 用来进行簇扩展的点
# min_points： 半径内最少的点数
def expand_cluster(dists, labs, cluster_id, seeds, eps, min_points):
    
    
    i = 0
    while i< len(seeds):
        # 获取一个临近点
        Pn = seeds[i]
        # 如果该点被标记为NOISE 则重新标记
        if labs[Pn] == NOISE:
            labs[Pn] = cluster_id
        # 如果该点没有被标记过
        elif labs[Pn] == UNCLASSIFIED:
            # 进行标记，并计算它的临近点 new_seeds
            labs[Pn] = cluster_id
            new_seeds = find_points_in_eps(Pn,eps,dists)
            
            # 如果 new_seeds 足够长则把它加入到seed 队列中
            if len(new_seeds) >=min_points:
                seeds = seeds + new_seeds
        
        i = i+1
        
        
def dbscan(datas, eps, min_points):
    
    # 计算 所有点之间的距离
    dists = getDistanceMatrix(datas)
    
    
    # 将所有点的标签初始化为UNCLASSIFIED
    n_points = datas.shape[0]
    labs = [UNCLASSIFIED]*n_points
    
    cluster_id = 0
    # 遍历所有点
    for point_id in range(0, n_points):
        # 如果当前点已经处理过了
        if not(labs[point_id] == UNCLASSIFIED):
            continue
            
        # 没有处理过则计算临近点
        seeds = find_points_in_eps(point_id,eps,dists)
        
        # 如果临近点数量过少则标记为 NOISE
        if len(seeds)

效果