比较全的深度学习数据预处理方法

1、中心化/零均值化

• 零均值化就是将每一维原始数据减去每一维数据的平均值，将结果代替原始数据

• ​在深度学习中，一般我们会把喂给网络模型的训练图片进行预处理，使用最多的方法就是零均值化(zero-mean) / 中心化，简单说来，它做的事情就是，对待训练的每一张图片的特征，都减去全部训练集图片的特征均值，这么做的直观意义就是，我们把输入数据各个维度的数据都中心化到0了。几何上的展现是可以将数据的中心移到坐标原点。如下图中zero-centered data（当然，其实这里也有不同的做法：我们可以直接求出所有像素的均值，然后每个像素点都减掉这个相同的值；稍微优化一下，我们可以在RGB三个颜色通道分别做这件事）

程序代码

例1：

import numpy as np
import matplotlib.pyplot as plt
from numpy import random

x = random.rand(50,2)     #随机生成一个50*2（50个样本，2维）的实数矩阵
print(x)
plt.scatter(x[:,1],x[:,0],color="red")  #以x的第二列为各点的横坐标，第一列为纵坐标
new_ticks = np.linspace(-1, 1, 5)     #固定坐标轴在-1到1之间，共5个值
plt.xticks(new_ticks)
plt.yticks(new_ticks)
plt.savefig('./ 均值化.jpg')
plt.show()

#***************零值化******************#
x -= np.mean(x,axis = 0)  #去均值
print(x)

plt.scatter(x[:,1],x[:,0],color="black")
new_ticks = np.linspace(-1, 1, 5)
plt.xticks(new_ticks)
plt.yticks(new_ticks)
plt.show()

2、标准化/归一化

归一化就是将原始数据归一到相同尺度，就是要把你需要处理的数据经过处理后（通过某种算法）限制在你需要的一定范围内，下面有几种方法来实现归一化，：

• （1）原始数据除以数据绝对值的最大值，以保证所有的数据归一化后都在-1到1之间。

• （2）原始数据零均值后，再将每一维的数据除以每一维数据的标准差（Z-score标准化方法）

${\mathrm{x}}^{\ast }=\frac{x-u}{\sigma }$

​ ①本方法要求原始数据的分布近似为高斯分布，否则归一化的效果会比较差

​ ②应用场景:在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，Z-score standardization表现更好。

• （3）最大最小标准化，使数据归一化到[0,1]之间，

$x\prime =\frac{x-\min (x)}{\max (x)-\min (x)}$

​ ①该方法适合用于数值比较集中的情况；缺陷：如果max和min不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不稳定。实际使用中可以用经验常量来替代max和min。

​ ②应用场景：在不涉及距离度量、协方差计算、数据不符合正态分布的时候，可以使用该方法或其他归一化方法（不包括Z-score方法）。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围

• （4）非线性归一化

  ​ 本归一化方法经常用在数据分化比较大的场景，有些数值很大，有些很小。通过一些数学函数，将原始值进行映射， 该方法包括 log，正切等，需要根据数据分布的情况，决定非线性函数的曲线：

  ​ ①log对数函数转换方法

  ​ y = log10(x)，即以10为底的对数转换函数，对应的归一化方法为：x’ = log10(x) /log10(max)，其中max表示样本数据的最大值，并且所有样本数据均要大于等于1.

  ​ ②atan反正切函数转换方法

  ​ 利用反正切函数可以实现数据的归一化，即x’ = atan(x)*(2/pi)，使用这个方法需要注意的是如果想映射的区间为[0，1]，则数据都应该大于等于0，小于0的数据将被映射到[－1，0]区间上.

  ​ ③L2范数归一化方法
  L2范数归一化就是特征向量中每个元素均除以向量的L2范数,
  向量
  $X(x_1,x_2,...,x_n)$ $L^2$的范数定义为：
  $norm(x)=\sqrt{{x_1}^2+{x_2}^2+..+{x_n}^2}$，要使得x归一化到单位 $L^2$范数，即建立一个从x到x’的映射，使得x’的 $L^2$范数为1,则：
  $\begin{array}{l}1=\mathrm{n}\mathrm{o}\mathrm{r}m(x\prime )\\ =\frac{\sqrt{{x_1}^2+{x_2}^2+..+{x_n}^2}}{norm(x)}\\ =\sqrt{\frac{{x_1}^2+{x_2}^2+..+{x_n}^2}{norm{(x)}^2}}\\ =\sqrt{{\left(\frac{x_1}{norm(x)}\right)}^2+{\left(\frac{x_2}{norm(x)}\right)}^2+...+{\left(\frac{x_n}{norm(x)}\right)}^2}\\ =\sqrt{x_1{{}^{\prime }}^2+x_2{{}^{\prime }}^2+...+x_n{{}^{\prime }}^2}\end{array}$
  即： ${x_i}^{\prime }=\frac{x_i}{norm(x)}$

程序代码

import numpy as np
import matplotlib.pyplot as plt
from numpy import random

x = random.rand(50,2)
# print(x)
plt.scatter(x[:,1],x[:,0],color="red")
new_ticks = np.linspace(-1, 1, 5)
plt.xticks(new_ticks)
plt.xticks(new_ticks)
plt.show()

#***************归一化******************#
x -= np.mean(x,axis = 0)  #去均值
x /= np.std(x)   #归一化             采用的方法（2）
x /= np.max(x)              #采用的方法（1）
#print(x)
plt.scatter(x[:,1],x[:,0],color="red")
new_ticks = np.linspace(-1, 1, 5)
plt.xticks(new_ticks)
plt.yticks(new_ticks)
plt.show()

（1）标准化与归一化的联系和差异

联系

标准化（Standardization）和归一化（Normalization）本质上都是对数据的线性变换，广义的说，你甚至可以认为他们是同一个母亲生下的双胞胎，因为二者都是不会改变原始数据排列顺序的线性变换；都能取消由于量纲不同引起的误差；都是对向量X按照比例压缩再进行平移。

差异

Normalization 会将数据映射到区间[0,1]或者[-1,1]中，仅由变量的极值决定，区间放缩法也是归一化的一种。而Standardization则是先通过零均值化（中心化）的方法然后除以标准差，把数据转换为均值是0，方差是1的标准正态分布，每个样本点都能给对标准化产生影响。

（2）为什么要归一化/标准化

无论是归一化还是标准化实质都是线性变换，线性变换有很多良好的性质，这些性质决定了对数据改变后不会造成“失效”，比如：线性变换不会改变原始数据的数值排序。

①某些模型求解需要

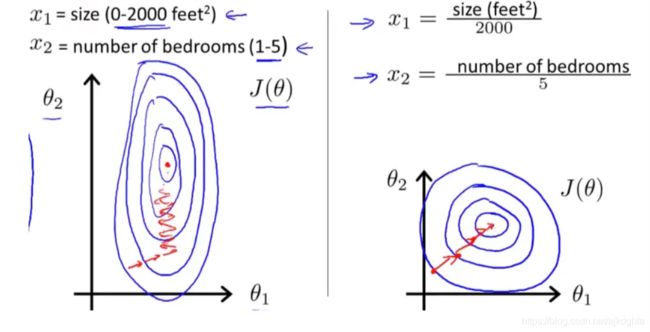
在使用梯度下降的方法求解最优化问题时， 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。如下图所示，蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征X1和X2的区间相差非常大，X1区间是[0,2000]，X2区间是[1,5]，其所形成的等高线非常尖。当使用梯度下降法寻求最优解时，很有可能走“之字型”路线（垂直等高线走），从而导致需要迭代很多次才能收敛；

而右图对两个原始特征进行了归一化，其对应的等高线显得很圆，在梯度下降进行求解时能较快的收敛。因此如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。

对于模型求解的理解也可以参考下面该篇文章：

---

---

下面来自文章来自知乎作者hitnlper忆臻

在给机器学习模型的数据中，对数据要进行归一化的处理。

为什么要进行归一化处理，下面从寻找最优解这个角度给出自己的看法。

假定为预测房价的例子，自变量为面积，房间数两个，因变量为房价。那么可以得到的公式为：
$$y={\theta }_1{x}_1+{\theta }_2{x}_2$$
​ 其中$x_1$代表房间数，${\theta }_1$代表$x_1$变量前面的系数。其中$x_2$代表面积，${\theta }_2$代表$x_2$变量前面的系数。首先我们写出两张图代表数据是否均一化的最优解寻解过程。

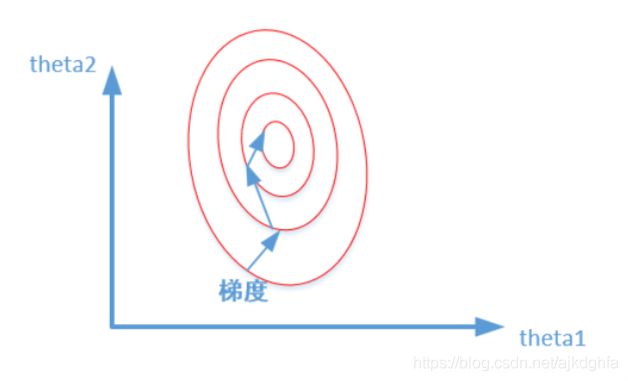
未归一化：

归一化之后：

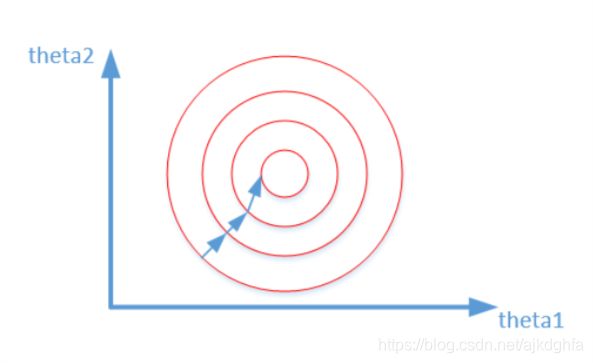
为什么会出现上述两个图，并且它们分别代表什么意思。我们在寻找最优解的过程也就是在使得损失函数值最小的theta1,theta2。

上述两幅图代码的是损失函数的等高线。我们很容易看出，当数据没有归一化的时候，面积数的范围可以从$0\sim 1000$，房间数的范围一般为0~10，可以看出面积数的取值范围远大于房间数。

影响

这样造成的影响就是在画损失函数的时候，数据没有归一化的表达式，可以为$J=(3{\theta }_1+600{\theta }_2-{\mathrm{y}}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}}{)}^2$，造成图像的等高线为类似椭圆形状，最优解的寻优过程就是像下图所示：

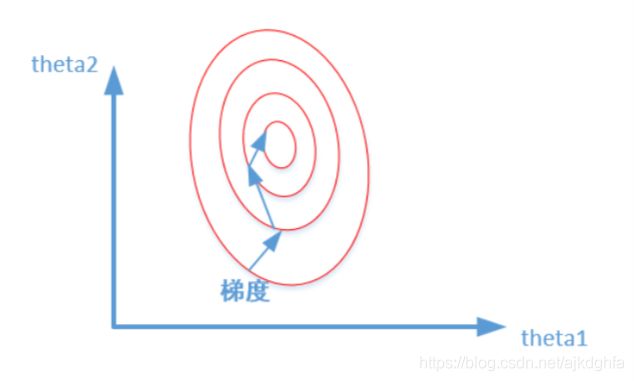
而数据归一化之后，损失函数的表达式可以表示为：
$J=(0.5{\theta }_1+0.55{\theta }_2-{\mathrm{y}}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}}{)}^2$，其中变量的前面系数几乎一样，则图像的等高线为类似圆形形状，最优解的寻优过程像下图所示：

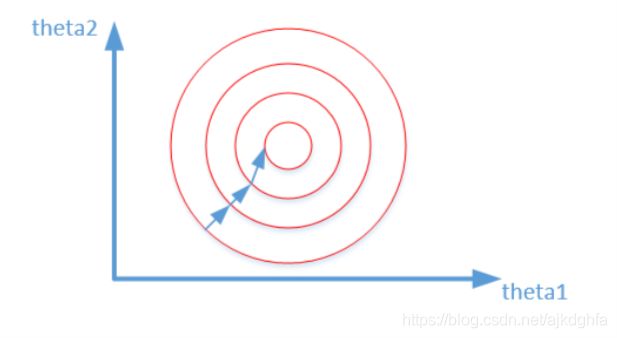
从上可以看出，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解。

---

---

②一些分类器需要计算样本之间的距离(如欧氏距离)，例如KNN。

如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)。

​ 例如：让一个成年人和一个儿童比拳击，显然不公平，因为成年人会力气会大一些，会更有胜算，那么此时已经造成了某个特征的影响程度大于另外一个，那么数据中如果主导特征引导的方向是正确的那么还好，如果方向是错的，也就是既梯度的更新方向是错的，那后面整个得到的结论都就被带跑偏了，训练出来的模型也就凉了）

所以说像这种数据差异大的情况要标准化/归一化，比如我同一个标准来度量谁的力量大，比如看看举起自身重量的多少倍？

③无量纲化

比如在预测房价的问题中，影响房价$y$的因素有房子面积$x_1$、卧室数量$x_2$等，我们得到的样本数据就是$(x_1,x_2)$这样一些样本点，这里的$x_1$,$x_2$又被称为特征。很显然，这些特征的量纲和数值得量级都是不一样的，在预测房价时，如果直接使用原始的数据值，那么他们对房价的影响程度将是不一样的，而通过标准化处理，可以使得不同的特征**具有相同的尺度（Scale）。**这样，在使用梯度下降法学习参数的时候，不同特征对参数的影响程度就一样了。

④ 避免数值问题

太大的数会引发数值问题。

（3）什么时候用归一化？什么时候用标准化？

（1） 在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好；（2） 在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

某知乎答主的回答提到了他个人经验： （1）如果对输出结果范围有要求，用归一化;（2）如果数据较为稳定，不存在极端的最大最小值，用归一化;（3）如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响。一般来说，个人建议优先使用标准哈。对于输出有要求时再尝试别的方法，如归一化或者更加复杂的方法。很多方法都可以将输出范围调整到[0, 1]，如果我们对于数据的分布有假设的话，更加有效的方法是使用相对应的概率密度函数来转换。让我们以高斯分布为例，我们可以首先计算高斯误差函数（Gaussian Error Function），此处定为er fc(·)，那么可以用下式进行转化：

$\max \left\{0,erfc\left(\frac{x-u}{\sigma \cdot \sqrt{2}}\right)\right\}$

​ 该简书作者也指出了哪些模型必须归一化/标准化？

​ （1）SVM。不同的模型对特征的分布假设是不一样的。比如SVM 用高斯核的时候，所有维度共用一个方差，这不就假设特征分布是圆的么，输入椭圆的就坑了人家，所以简单的归一化都还不够好，来杯白化才有劲。比如用树的时候就是各个维度各算各的切分点，没所谓。

​ （2）KNN。需要度量距离的模型，一般在特征值差距较大时，都会进行归一化/标准化。不然会出现“大数吃小数”。

​ （3）神经网络。
  ①数值问题
 归一化/标准化可以避免一些不必要的数值问题。输入变量的数量级未致于会引起数值问题吧，但其实要引起也并不是那么困难。因为tansig（tanh）的非线性区间大约在[-1.7，1.7]。意味着要使神经元有效，tansig( w1x1 + w2x2 +b) 里的 w1x1 +w2x2 +b 数量级应该在 1 （1.7所在的数量级）左右。这时输入较大，就意味着权值必须较小，一个较大，一个较小，两者相乘，就引起数值问题了。
 假如你的输入是421，你也许认为，这并不是一个太大的数，但因为有效权值大概会在1/421左右，例如0.00243，那么，在matlab里输入 421·0.00243 == 0.421·2.43，会发现不相等，这就是一个数值问题。

②求解需要
 a. 初始化：在初始化时我们希望每个神经元初始化成有效的状态，tansig函数在[-1.7, 1.7]范围内有较好的非线性，所以我们希望函数的输入和神经元的初始化都能在合理的范围内使得每个神经元在初始时是有效的。（如果权值初始化在[-1,1]且输入没有归一化且过大，会使得神经元饱和）
 b. 梯度：以输入-隐层-输出这样的三层BP为例，我们知道对于输入-隐层权值的梯度有2ew(1-a^2)*x的形式（e是誤差，w是隐层到输出层的权重，a是隐层神经元的值，x是输入），若果输出层的数量级很大，会引起e的数量级很大，同理，w为了将隐层（数量级为1）映身到输出层，w也会很大，再加上x也很大的话，从梯度公式可以看出，三者相乘，梯度就非常大了。这时会给梯度的更新带来数值问题。
 c. 学习率：由（2）中，知道梯度非常大，学习率就必须非常小，因此，学习率（学习率初始值）的选择需要参考输入的范围，不如直接将数据归一化，这样学习率就不必再根据数据范围作调整。 隐层到输出层的权值梯度可以写成 2ea，而输入层到隐层的权值梯度为 2ew(1-a^2)x ，受 x 和 w 的影响，各个梯度的数量级不相同，因此，它们需要的学习率数量级也就不相同。对w1适合的学习率，可能相对于w2来说会太小，若果使用适合w1的学习率，会导致在w2方向上步进非常慢，会消耗非常多的时间，而使用适合w2的学习率，对w1来说又太大，搜索不到适合w1的解。如果使用固定学习率，而数据没归一化，则后果可想而知。

3、PCA和白化

• PCA：主成成分分析，首先将数据变成0均值的，然后计算数据的协方差矩阵来得到数据不同维度之间的相关性，协方差矩阵的第(i,j)个元素表示数据第i维和第j维特征的相关性，特别地，对角线上的元素表示方差。另外，协方差矩阵是对称并且半正定的。可以对该协方差矩阵进行SVD分解，其中U矩阵的列为特征向量，S对角线上的元素是奇异值（等同于特征值的平方）。为了对数据去相关，首先将数据（0均值后的）投影到特征向量上，注意，U的列是相互正交的向量，也因此它们可以被看成基向量。这种投影相当于将数据X旋转、投影到新的基向量轴上。如果再去计算Xrot 的协方差矩阵的话，就会发现它是一个对角阵，说明不同维度之间不再相关。np.linalg.svd的一个很好的特性在于返回的U是按照其特征值的大小排序的，排在前面的就是主方向，因此可以通过选取前几个特征向量来减少数据的维度。

• 白化：把各个特征轴上的数据除以对应特征值，从而达到在每个特征轴上都归一化幅度的结果。也就是在PCA的基础上再除以每一个特征的标准差，以使其归一化，其标准差就是奇异值的平方根。

(1)数学原理理解（强烈建议大家点进去看一下！！！）

该博主对PCA的数学原理从头到尾进行的讲解，可以帮助大家进一步理解

• ** 强烈建议大家点进去看一下 **，

程序代码

import numpy as np
import matplotlib.pyplot as plt
from numpy import random

x = random.rand(50,2)    
# print(x)
plt.scatter(x[:,1],x[:,0],color="red")  
new_ticks = np.linspace(-1, 1, 5)
plt.xticks(new_ticks)
plt.yticks(new_ticks)
plt.show()

#***************PCA和白化***************#
x -= np.mean(x) # 去均值
cov = np.dot(x.T, x) / x.shape[0]   # 计算协方差矩阵得到相关性
U,S,V = np.linalg.svd(cov)       # 协方差矩阵奇异值分解
Xrot = np.dot(x, U)                # 去相关
Xrot_reduced = np.dot(x,U[:,:100]) # 降维
plt.scatter(Xrot_reduced[:,1],Xrot_reduced[:,0], color = "green")
new_ticks = np.linspace(-1, 1, 5)
plt.xticks(new_ticks)
plt.yticks(new_ticks)
plt.show()
#白化数据
Xwhite = Xrot / np.sqrt(S + 1e-5)
plt.scatter(Xwhite[:,1],Xwhite[:,0], color = "purple")
new_ticks = np.linspace(-1, 1, 5)
plt.xticks(new_ticks)
plt.yticks(new_ticks)
plt.show()

参考文献：
[1]https://blog.csdn.net/keeppractice/article/details/109280623

[2]https://zhuanlan.zhihu.com/p/81560511

[3]https://zhuanlan.zhihu.com/p/27627299

[4]https://www.zhihu.com/question/20455227/answer/370658612

[5]http://blog.codinglabs.org/articles/pca-tutorial.html

[6]https://www.jianshu.com/p/95a8f035c86c
[7]https://blog.csdn.net/llyj_/article/details/87606704