损失函数统计

L1 Loss

最常看到的MAE也是指L1 Loss损失函数。 它是把目标值 与模型输出（估计值） 做绝对值得到的误差。由于神经网络通常是解决复杂问题，所以很少使用。
$$\mathrm{loss}(x,y)=\frac{1}{n}\sum _{i=1}^n\left|y_i-f\left(x_i\right)\right|$$

L2 Loss

最常看到的MSE也是指L2 Loss损失函数，PyTorch中将其命名为torch.nn.MSELoss。它是把目标值 与模型输出（估计值） 做差然后平方得到的误差。

$$\mathrm{loss}(x,y)=\frac{1}{n}\sum _{i=1}^n{\left(y_i-f\left(x_i\right)\right)}^2$$

Smooth L1 Loss

$$l_n=\{\begin{array}{ll}0.5\ast {\left(x_n-y_n\right)}^2/\text{ beta },& \text{ if }\left|x_n-y_n\right|<\text{ beta }\\ \left|x_n-y_n\right|-0.5\ast \text{ beta, }& \text{ otherwise }\end{array}$$

torch.nn.SmoothL1Loss()

我们直接看那个loss计算公式 ,可以发现，是一个分段函数，我们将绝对值差视为一个变量z，那么这个变量是大于0的，即分段函数只在大于等于0处有定义，有图像。我们再来看看分段点，就是beta。

有意思的是，在分段函数和这个分段点有关，在第一个公式（左边分段函数）中，函数值小于等于0.5z ，因为除了beta。右边分段函数中，大于等于0.5z。所以是连续的，所以叫做Smooth。

而且beta固定下来的时候，当z很大时，损失是线性函数，也就是说损失不会像MSE那样平方倍的爆炸。

NLL Loss

负对数似然损失，主要应用在分类任务中。它先通过logSoftmax()，然后把label对应的输出值拿出来，负号去掉，然后平均。

torch.nn.NLLLoss()

CrossEntropy Loss

交叉熵，实际上它是由nn.LogSoftmax()和nn.NLLLoss()组成。 主要应用在多分类的问题中(二分类也可以用)

torch.nn.CrossEntropyLoss()

BCELoss

BCE Loss就是二分类的交叉熵(它才是严格按照交叉熵的公式去算的，但只针对二分类) BCEloss一般应用在单标签二分类和多标签二分类中。

$$\mathrm{loss}F=-\frac{1}{n}\sum \left(y_n\times \mathrm{In}{x}_n+\left(1-y_n\right)\times \mathrm{In}\left(1-x_n\right)\right)$$

一般要先sigmoid再bceloss，也可使用torch.nn.BCEWithLogitsLoss，将Sigmoid层和BCELoss 组合在一个类中，这个版本比使用简单的Sigmoid 后跟BCELoss在数值上更稳定。

Focal Loss

$$FL=\{\begin{array}{ll}-\alpha (1-p{)}^{\gamma }\log (p),& \text{ if }y=1\\ -(1-\alpha )p^{\gamma }\log (1-p),& \text{ if }y=0\end{array}$$

import torch
import torch.nn.functional as F


def reduce_loss(loss, reduction):
    reduction_enum = F._Reduction.get_enum(reduction)
    # none: 0, elementwise_mean:1, sum: 2
    if reduction_enum == 0:
        return loss
    elif reduction_enum == 1:
        return loss.mean()
    elif reduction_enum == 2:
        return loss.sum()


def weight_reduce_loss(loss, weight=None, reduction='mean', avg_factor=None):
    if weight is not None:
        loss = loss * weight

    if avg_factor is None:
        loss = reduce_loss(loss, reduction)
    else:
        # if reduction is mean, then average the loss by avg_factor
        if reduction == 'mean':
            loss = loss.sum() / avg_factor
        # if reduction is 'none', then do nothing, otherwise raise an error
        elif reduction != 'none':
            raise ValueError('avg_factor can not be used with reduction="sum"')
    return loss


def py_sigmoid_focal_loss(pred, target, weight=None, gamma=2.0, alpha=0.25, reduction='mean', avg_factor=None):
    # 注意 输入的pred不需要经过sigmoid
    pred_sigmoid = pred.sigmoid()
    target = target.type_as(pred)
    pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)
    focal_weight = (alpha * target + (1 - alpha) *
                    (1 - target)) * pt.pow(gamma)
    # 下面求交叉熵的这个函数 对pred进行了sigmoid
    loss = F.binary_cross_entropy_with_logits(
        pred, target, reduction='none') * focal_weight
    # print(loss)
    '''输出
    tensor([[0.0394, 0.0506],
        [0.3722, 0.0043]])
        '''
    loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
    return loss

IoU Loss

$$L_{IoU}=1-IoU$$

优点：

1. IoU作为距离时是一个度量。因为它包含了作为度量的所有属性，比如：非负性，不确定性对称性和三角不等性。
2. IoU有尺度不变性，这意味着任意两个方框Ａ和Ｂ的相似性与他们的空间尺度的无关。

缺点：

1. 如果两个目标没有重叠，IoU将会为０,并且不会反应两个目标之间的距离，在这种无重叠目标的情况下，如果IoU用作于损失函数，梯度为０，无法优化。
2. IoU无法区分两个对象之间不同的对齐方式。更确切地讲，不同方向上有相同交叉级别的两个重叠对象的IoU会完全相等。如下图
   

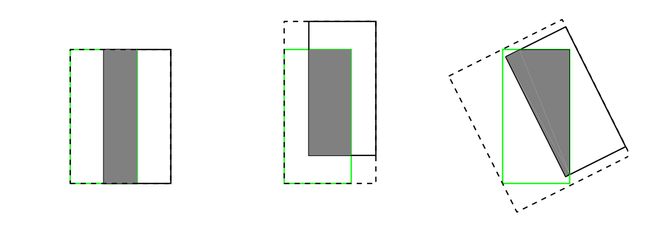
GIoU Loss

对于任意的两个Ａ、B框，首先找到一个能够包住它们的最小方框Ｃ。然后计算C \ (A ∪ B) 的面积与Ｃ的面积的比值，注：C \ (A ∪ B) 的面积为C的面积减去A∪B的面积。再用Ａ、Ｂ的IoU值减去这个比值得到GIoU。

$$GIoU=\frac{|A\cap B|}{|A\cup B|}-\frac{|C\backslash (A\cup B)|}{|C|}=IoU-\frac{|C\backslash (A\cup B)|}{|C|}$$
$${\mathcal{L}}_{GIoU}=1-GIoU$$

DIoU Loss

$$L_{DIoU}=1-IoU+\frac{p^2\left(b,b_{gt}\right)}{c^2}$$

$\frac{p^2\left(b,b_{gt}\right)}{c^2}$代表了预测框和真实框中心点的直线距离的平方，c代表能够同时包含两个框的最小闭包区域的对角线距离。

CIoU Loss

$$CIoU=IoU-\frac{{\rho }^2(b,b^{gt})}{c^2}-\alpha v$$
$$\alpha =\frac{v}{1-IoU+v}$$
$$v=\frac{4}{{\pi }^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}{)}^2$$
$$L_{CIoU}=1-CIoU$$

https://zhuanlan.zhihu.com/p/83131026 l1 l2 smoothl1

https://blog.csdn.net/qq_43391414/article/details/121740411 smoothl1

https://www.cnblogs.com/picassooo/p/12600046.html kl 散度和交叉熵

https://zhuanlan.zhihu.com/p/340585479 各种loss

https://blog.csdn.net/weixin_41735859/article/details/89288493 GIoU

https://www.cnblogs.com/xuanyuyt/p/12090694.html iou

https://blog.csdn.net/liangdong2014/article/details/114380202 iou