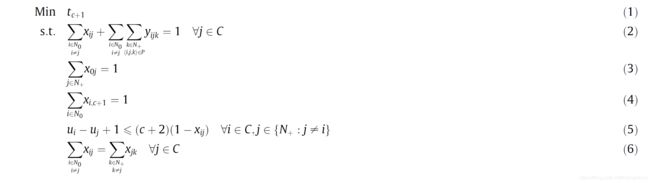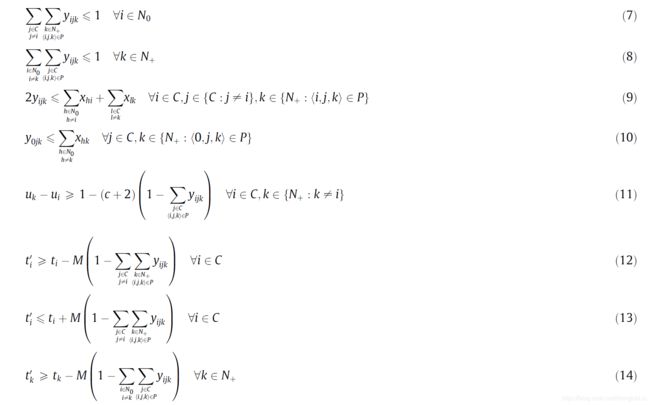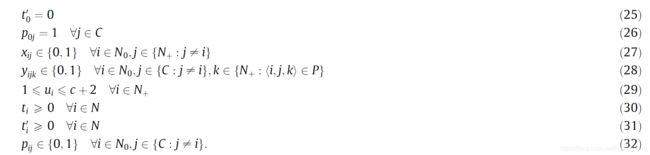论文代码复现 | 无人机与卡车联合配送(Python+Gurobi)(The flying sidekick traveling salesman problem)
文章目录
- 论文代码复现 | 无人机与卡车联合配送(Python+Gurobi)(The flying sidekick traveling salesman problem)
-
- 无人机配送概述
- 文献笔记
-
- 论文摘要
- 论文主要图表摘录
-
- 无人机与卡车联合运输 - 联合但无交互的模式
- 无人机与卡车联合运输 - 联合有交互的模式
- 无人机与卡车联合运输(FSTSP)的数学模型
- Python调用Gurobi求解FSTSP
- 数值实验
-
- 算例
- 结果展示与可视化
-
- 设置`nodeNum = 5`
- 设置`nodeNum = 7`
- 设置`nodeNum = 8`
- 设置`nodeNum = 10`
- 拓展
- 参考文献
论文代码复现 | 无人机与卡车联合配送(Python+Gurobi)(The flying sidekick traveling salesman problem)
无人机配送概述
随着无人机技术的不断发展,无人机在工业界的应用场景也日益多样化。近几年,很多物流企业开始将目光瞄向无人机配送。比如亚马逊、DHL、京东、顺丰等。渐渐的,这种配送模式得到了更大的扩展,现如今,很多企业都在使用无人配送的提法,在这种无人配送的场景中, 无人配送小车、无人机是重要的组成部分。本文主要关注无人机配送。
无人机配送的模式多种多样。
第一种就是在城市中选择若
干个无人机起飞点,在这个点的无人机从改点出发,去配送周围的客户。
另一种是无人机和卡车联合配送的模式。这种模式也有很多不同的操作方法。
卡车司机带着无人机一起去配送(flying sidekick TSP, FDTSP),到一些比较难服务的点,就让无人机去配送那个点,然后自己去下一个客户点。无人机配送完后,卡车司机再遥控无人机跟卡车司机会合。卡车司机不带无人机(parallel drone scheduling TSP, PDTSP)。我们分配任务的时候,决策哪些任务交给无人机去服务,哪些任务交给卡车去服务,然后各自规划自己的服务顺序,最终把所有顾客都服务完。期间,卡车和无人机没有交互。
当然还有其他服务方式。这里不做展开。
文献笔记
本文主要是发表在Transportation Research Part C: Emerging Technologies上的关于无人机和卡车的协同配送的文章的模型部分的代码复现。文章题目为The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery(参考文献[1])
Murray, C. C., & Chu, A. G. (2015).
The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transportation Research Part C: Emerging Technologies, 54, 86-109.
该问题简称FSTSP。
论文摘要
Once limited to the military domain, unmanned aerial vehicles are now poised to gain widespread adoption in the commercial sector. One such application is to deploy these aircraft, also known as drones, for last-mile delivery in logistics operations. While significant research efforts are underway to improve the technology required to enable delivery by drone, less attention has been focused on the operational challenges associated with leveraging this technology. This paper provides two mathematical programming models aimed at optimal routing and scheduling of unmanned aircraft, and delivery trucks, in this new paradigm of parcel delivery. In particular, a unique variant of the classical vehicle routing problem is introduced, motivated by a scenario in which an unmanned aerial vehicle works in collaboration with a traditional delivery truck to distribute parcels. We present mixed integer linear programming formulations for two delivery-by-drone problems, along with two simple, yet effective, heuristic solution approaches to solve problems of practical size. Solutions to these problems will facilitate the adoption of unmanned aircraft for last-mile delivery. Such a delivery system is expected to provide faster receipt of customer orders at less cost to the distributor and with reduced environmental impacts. A numerical analysis demonstrates the effectiveness of the heuristics and investigates the tradeoffs between using drones with faster flight speeds versus longer endurance.
论文主要图表摘录
下面我们讲论文中的一些重要的图摘录下来,帮助读者快速理解文章的内容。首先就是亚马逊和DHL的无人机携带包裹的场景。

无人机与卡车联合运输 - 联合但无交互的模式
下面几幅图中
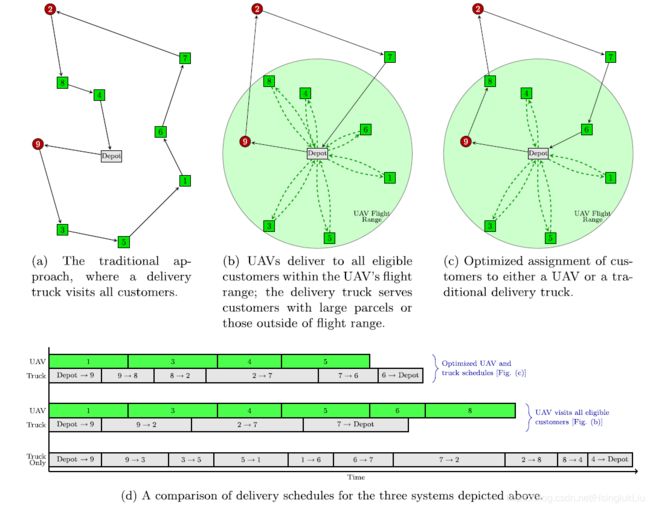
绿色方框 – 代表在无人机飞行里程范围内的客户点,这些点都可以被无人机服务;
红色圆点 – 代表在无人机里程范围之外的客户点,这些点只能被卡车服务,不能被无人机服务。
图a是传统的配送模式,卡车按照访问顺序,从出发点依次服务完所有的顾客点。
图b是卡车和无人机联合配送的场景,但是卡车和无人既没有互动。可以看到,顾客2和顾客9是无法被无人机服务的点,而其余的点都是可以被无人机服务的。一个可行解就是:
- 卡车的服务顺序
depot→ 9 → 2 → 7 → \rightarrow 9 \rightarrow 2 \rightarrow 7 \rightarrow →9→2→7→depot - 无人机服务的点为:1、3、4、5、6、7、8。每个点无人机都往返依次完成服务。
图c是经过优化的最优配送方案。
无人机与卡车联合运输 - 联合有交互的模式
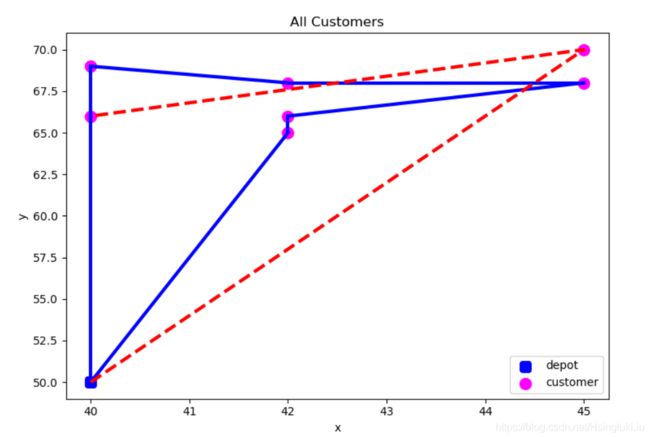
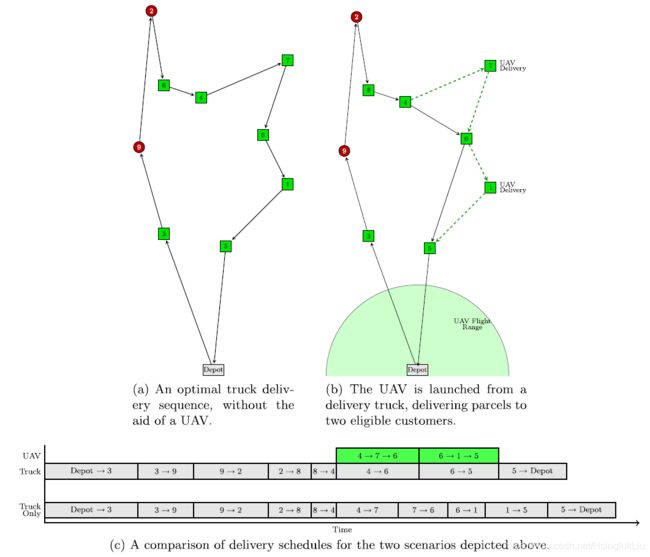
下图 a是卡车单独运输的最优解。
图b是无人机和卡车联合配送有交互的最优解。可以看到,卡车在配送到客户点4的时候,放飞了无人机,让无人机去服务客户点7,之后又在客户点6放飞了无人机去服务客户点1。分别在客户点6和客户点5回收无人机。(当然是同一架无人机)
无人机与卡车联合运输(FSTSP)的数学模型
卡车司机带着无人机一起去配送(flying sidekick TSP, FDTSP),到一些比较难服务的点,就让无人机去配送那个点,然后自己去下一个客户点。无人机配送完后,卡车司机再遥控无人机跟卡车司机会合。
这里最主要的决策变量有两个:
x i j x_{ij} xij:
0-1变量。表示卡车是否从点 i i i直接运行到点 j j j;
y i j k y_{ijk} yijk:0-1变量。如果无人机从点 i i i被发射,去服务客户点 j j j,然后在客户点 k k k被回收, 则 y i j k = 1 y_{ijk}=1 yijk=1,否则为0。这里论文中强调,收发、访问点互不相同,也就是 i , j , k i,j,k i,j,k互不相同。
t i t_i ti:到达顾客点 i i i的时间;
u i u_i ui:为了消除子环路,也可以看做是第 i i i个客户点的访问顺序,也就是他是第几个被访问的;
重要参数
- 无人机的单次发射时间;
- 无人机的回收时间;
这些时间可以自己设置。另外,无人机的飞行速度、卡车的行驶速度等,都可以自己进行设置测试。
目标函数:最小化服务完所有顾客的时间。
接下来,我们贴上该问题的数学模型。数学模型的具体解释请读者自行读论文,这里我们就不在赘述。
Python调用Gurobi求解FSTSP
这里我们贴上Python调用Gurobi求解FSTSP的完整代码。代码中包含了可视化最优解的部分,方便读者查看最优解的情况。
# _*_coding:utf-8 _*_
from __future__ import print_function
from gurobipy import *
import re
import math
# from test.pickletester import BigmemPickleTests
import matplotlib.pyplot as plt
import numpy
import pandas as pd
class Data:
customerNum = 0
nodeNum = 0
range = 0
lunchingTime= 0
recoverTime = 0
cor_X = []
cor_Y = []
demand = []
serviceTime = []
readyTime = []
dueTime = []
disMatrix = [[]] # 读取数据
# function to read data from .txt files
def readData(data, path, customerNum):
data.customerNum = customerNum
data.nodeNum = customerNum + 2
f = open(path, 'r')
lines = f.readlines()
count = 0
# read the info
for line in lines:
count = count + 1
if(count == 2):
line = line[:-1]
str = re.split(r" +", line)
data.range = float(str[0])
elif(count == 5):
line = line[:-1]
str = re.split(r" +", line)
data.lunchingTime = float(str[0])
data.recoverTime = float(str[1])
elif(count >= 9 and count <= 9 + customerNum): # (count >= 9 and count <= 9 + customerNum)
line = line[:-1]
str = re.split(r" +", line)
data.cor_X.append(float(str[2]))
data.cor_Y.append(float(str[3]))
data.demand.append(float(str[4]))
data.readyTime.append(float(str[5]))
data.dueTime.append(float(str[6]))
data.serviceTime.append(float(str[7]))
data.cor_X.append(data.cor_X[0])
data.cor_Y.append(data.cor_Y[0])
data.demand.append(data.demand[0])
data.readyTime.append(data.readyTime[0])
data.dueTime.append(data.dueTime[0])
data.serviceTime.append(data.serviceTime[0])
# compute the distance matrix
data.disMatrix = [([0] * data.nodeNum) for p in range(data.nodeNum)] # 初始化距离矩阵的维度,防止浅拷贝
# data.disMatrix = [[0] * nodeNum] * nodeNum] 这个是浅拷贝,容易重复
for i in range(0, data.nodeNum):
for j in range(0, data.nodeNum):
temp = (data.cor_X[i] - data.cor_X[j])**2 + (data.cor_Y[i] - data.cor_Y[j])**2
data.disMatrix[i][j] = math.sqrt(temp)
# if(i == j):
# data.disMatrix[i][j] = 0
# print("%6.2f" % (math.sqrt(temp)), end = " ")
temp = 0
return data
def printData(data, customerNum):
print("下面打印数据\n")
print("UAV range = %4d" % data.range)
print("UAV lunching time = %4d" % data.lunchingTime)
print("UAV recover time = %4d" % data.recoverTime)
for i in range(len(data.demand)):
print('{0}\t{1}\t{2}\t{3}'.format(data.demand[i], data.readyTime[i],data.dueTime[i], data.serviceTime[i]))
print("-------距离矩阵-------\n")
for i in range(data.nodeNum):
for j in range(data.nodeNum):
#print("%d %d" % (i, j))
print("%6.2f" % (data.disMatrix[i][j]), end = " ")
print()
class Solution:
ObjVal = 0
X = [[]]
Y = [[[]]]
U = []
P = []
T = []
Tt = []
route_Truck = []
route_UAV = []
# def __init__(self):
# solution = Solution()
# # X_ij
# solution.X = [[[] for i in range(data.nodeNum)] for j in range(data.nodeNum)]
# # Y_ijk
# solution.Y = [[[[] for k in range(data.nodeNum)] for j in range(data.nodeNum)] for i in range(data.nodeNum)]
# # U_i
# solution.U = [[] for i in range(data.nodeNum)]
# # P_ij
# solution.P = [[[] for j in range(data.nodeNum)] for i in range(data.nodeNum)]
# # T_i, T_i'
# solution.T = [[] for i in range(data.nodeNum)]
# solution.Tt = [[] for i in range(data.nodeNum)]
# return solution
def getSolution(self, data, model):
solution = Solution()
solution.ObjVal = model.ObjVal
# X_ij
solution.X = [([0] * data.nodeNum) for j in range(data.nodeNum)]
# Y_ijk
solution.Y = [[([0] * data.nodeNum) for j in range(data.nodeNum)] for i in range(data.nodeNum)]
# U_i
solution.U = [[0] for i in range(data.nodeNum)]
# P_ij
solution.P = [[[0] for j in range(data.nodeNum)] for i in range(data.nodeNum)]
# T_i, T_i'
solution.T = [[0] for i in range(data.nodeNum)]
solution.Tt = [[0] for i in range(data.nodeNum)]
a = U[0].x
for m in model.getVars():
str = re.split(r"_", m.VarName)
if(str[0] == "X" and m.x == 1):
solution.X[int(str[1])][int(str[2])] = m.x
print(str, end = "")
print(" = %d" % m.x)
elif(str[0] == "Y" and m.x == 1):
solution.Y[int(str[1])][int(str[2])][int(str[3])] = m.x
elif(str[0] == "U" and m.x > 0) :
solution.U[int(str[1])] = m.x
elif(str[0] == "T" and m.x > 0):
solution.T[int(str[1])] = m.x
elif(str[0] == "Tt" and m.x > 0):
solution.Tt[int(str[1])] = m.x
elif(str[0] == "P" and m.x > 0):
solution.P[int(str[1])][int(str[2])] = m.x
# get the route of truck and UAV
j = 0
for i in range(data.nodeNum):
i = j # note that the variable is whether is a local variable or a global variable
# print("i = %d, j = %d" % (i, j), end = " ")
for j in range(data.nodeNum):
if(solution.X[i][j] == 1):
solution.route_Truck.append(i)
print(" %d -" % i, end = " ")
# print(" i = %d, j = %d" % (i, j))
break
print(" 0")
solution.route_Truck.append(0)
print("\n\n ------Route of UAV ------- ")
count = 0
for i in range(data.nodeNum):
for j in range(data.nodeNum):
for k in range(data.nodeNum):
if(solution.Y[i][j][k] == 1):
count = count + 1
#print("UAV %d : %d - %d - %d" % (count, i, j, k))
temp = [i, j, k]
solution.route_UAV.append(temp)
for i in range(len(solution.route_Truck)):
print(" %d " % solution.route_Truck[i], end = " ")
print()
print("\n\n ------Route of UAV ------- ")
for i in range(len(solution.route_UAV)):
for j in range(len(solution.route_UAV[0])):
print("UAV %d : %d - %d - %d" % (i, solution.route_UAV[i][0], solution.route_UAV[i][1], solution.route_UAV[i][2]))
# print(solution.route_UAV)
return solution
# reading data
data = Data()
# path = r'C:\Users\hsingluLiu\eclipse-workspace\PythonCallGurobi_Applications\FSTSP\c101.txt'
path = 'c101.txt'
customerNum = 10
readData(data, path, customerNum)
printData(data, customerNum)
# =========build the model===========
big_M = 10000
# construct the model object
model = Model("FSTSP")
# Initialize variables
# create variables: Muiti-dimension vector: from inner to outer
# X_ij
X = [[[] for i in range(data.nodeNum)] for j in range(data.nodeNum)]
# Y_ijk
Y = [[[[] for k in range(data.nodeNum)] for j in range(data.nodeNum)] for i in range(data.nodeNum)]
# U_i
U = [[] for i in range(data.nodeNum)]
# P_ij
P = [[[] for j in range(data.nodeNum)] for i in range(data.nodeNum)]
# T_i, T_i'
T = [[] for i in range(data.nodeNum)]
Tt = [[] for i in range(data.nodeNum)]
for i in range(data.nodeNum):
name1 = 'U_' + str(i)
name2 = 'T_' + str(i)
name3 = 'Tt_' + str(i)
U[i] = model.addVar(0, data.nodeNum, vtype = GRB.CONTINUOUS, name = name1)
T[i] = model.addVar(0, big_M, vtype = GRB.CONTINUOUS, name = name2)
Tt[i] = model.addVar(0, big_M, vtype = GRB.CONTINUOUS, name = name3)
for j in range(data.nodeNum):
name4 = 'X_' + str(i) + "_"+ str(j)
name5 = 'P_' + str(i) + "_" + str(j)
X[i][j] = model.addVar(0, 1, vtype = GRB.BINARY, name = name4)
P[i][j] = model.addVar(0, 1, vtype = GRB.BINARY, name = name5)
for k in range(data.nodeNum):
name6 = 'Y_' + str(i) + "_" + str(j) + "_" + str(k)
Y[i][j][k] = model.addVar(0, 1, vtype = GRB.BINARY, name = name6)
# Add constraints
# create the objective expression(1)
obj = LinExpr(0)
# add the objective function into the model
model.setObjective(T[data.nodeNum - 1], GRB.MINIMIZE)
# constraint (2)
for j in range(1, data.nodeNum - 1): # 这里需要注意,i的取值范围,否则可能会加入空约束
expr = LinExpr(0)
for i in range(0, data.nodeNum - 1): # i -- N0
if(i != j):
expr.addTerms(1, X[i][j])
for k in range(1, data.nodeNum): # k -- N+
if(i != k and j != k):
expr.addTerms(1, Y[i][j][k])
model.addConstr(expr == 1, "c1")
expr.clear()
# constraint (3)
expr = LinExpr(0)
for j in range(1, data.nodeNum):
expr.addTerms(1, X[0][j])
model.addConstr(expr == 1, "c2")
expr.clear()
# constraint (4)
expr = LinExpr(0)
for i in range(data.nodeNum - 1):
expr.addTerms(1, X[i][data.nodeNum - 1])
model.addConstr(expr == 1.0, "c3")
expr.clear()
# constraint (5)
for i in range(1, data.nodeNum - 1):
for j in range(1, data.nodeNum):
if(i != j):
model.addConstr(U[i] - U[j] + 1 <= big_M - big_M * X[i][j], 'c5')
# constraint (6)
for j in range(1, data.nodeNum - 1):
expr1 = LinExpr(0)
expr2 = LinExpr(0)
for i in range(0, data.nodeNum - 1):
if(j != i):
expr1.addTerms(1, X[i][j])
for k in range(1, data.nodeNum):
if(j != k):
expr2.addTerms(1, X[j][k])
model.addConstr(expr1 == expr2, "c6")
expr1.clear()
expr2.clear()
# constraint (7)
for i in range(data.nodeNum - 1):
expr = LinExpr(0)
for j in range(1, data.nodeNum - 1):
if(i != j ):
for k in range(1, data.nodeNum):
if(i != k and j != k):
expr.addTerms(1, Y[i][j][k])
model.addConstr(expr <= 1, 'c7')
expr.clear()
# constraint (8)
for k in range(1, data.nodeNum):
expr = LinExpr(0)
for i in range(0, data.nodeNum - 1):
if(i != k ):
for j in range(1, data.nodeNum - 1):
if(j != i and j != k):
expr.addTerms(1, Y[i][j][k])
model.addConstr(expr <= 1, 'c8')
expr.clear()
# constraint (9)
for i in range(1, data.nodeNum - 1):
for j in range(1, data.nodeNum):
for k in range(1, data.nodeNum):
if(i != j and i != k and j != k):
expr1 = LinExpr(0)
expr2 = LinExpr(0)
for h in range(data.nodeNum - 1):
if(h != i):
expr1.addTerms(1, X[h][i])
for l in range(1, data.nodeNum - 1):
if(l != k):
expr2.addTerms(1, X[l][k])
model.addConstr(2 * Y[i][j][k] <= expr1 + expr2, "c9")
expr1.clear()
expr2.clear()
# constraint (10)
for j in range(1, data.nodeNum - 1):
for k in range(1, data.nodeNum):
if(j != k):
expr = LinExpr(0)
for h in range(1, data.nodeNum - 1):
expr.addTerms(1, X[h][k])
model.addConstr(Y[0][j][k] <= expr, "c10")
expr.clear()
# constraint (11)
for i in range(1, data.nodeNum - 1):
for k in range(1, data.nodeNum):
if(k != i):
expr = LinExpr(0)
for j in range(1, data.nodeNum - 1):
if(i != j and j != k):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(U[k] - U[i] >= 1 - big_M + expr, "c11")
expr.clear()
# constraint (12)
for i in range(1, data.nodeNum - 1):
expr = LinExpr(0)
for j in range(1, data.nodeNum - 1):
for k in range(1, data.nodeNum):
if(j != i and i != k and j != k):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(Tt[i] >= T[i] - big_M + expr, "c12")
expr.clear()
# constraint (13)
for i in range(1, data.nodeNum - 1):
expr = LinExpr(0)
for j in range(1, data.nodeNum - 1):
for k in range(1, data.nodeNum):
if(j != i and i != k and j != k):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(Tt[i] <= T[i] + big_M - expr, "c13")
expr.clear()
# constraint (14)
for k in range(1, data.nodeNum):
expr = LinExpr(0)
for i in range(0, data.nodeNum - 1):
for j in range(1, data.nodeNum - 1):
if(j != i and i != k and j != k):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(Tt[k] >= T[k] - big_M + expr, "c14")
expr.clear()
# constraint (15)
for k in range(1, data.nodeNum):
expr = LinExpr(0)
for i in range(0, data.nodeNum - 1):
for j in range(1, data.nodeNum - 1):
if(j != i and i != k and j != k):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(Tt[k] <= T[k] + big_M - expr, "c15")
expr.clear()
# constraint (16)
for h in range(data.nodeNum - 1):
for k in range(1, data.nodeNum):
if(h != k):
expr1 = LinExpr(0)
expr2 = LinExpr(0)
for l in range(1, data.nodeNum - 1):
for m in range(1, data.nodeNum):
if(k != l and k != m and l != m):
expr1.addTerms(data.lunchingTime, Y[k][l][m])
for i in range(data.nodeNum - 1):
for j in range(1, data.nodeNum - 1):
if(i != j and i != k and j != k):
expr2.addTerms(data.recoverTime, Y[i][j][k])
model.addConstr(T[k] >= T[h] + data.disMatrix[h][k] + expr1 + expr2 - big_M + big_M * X[h][k], "c16")
expr1.clear()
expr2.clear()
# constraint (17)
for j in range(1, data.nodeNum - 1):
for i in range(data.nodeNum - 1):
if(i != j):
expr = LinExpr(0)
for k in range(1, data.nodeNum):
if(i != k and j != k):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(Tt[j] >= Tt[i] + data.disMatrix[i][j] - big_M + expr, "c17")
expr.clear()
# constraint (18)
for j in range(1, data.nodeNum - 1):
for k in range(1, data.nodeNum):
if(k != j):
expr = LinExpr(0)
for i in range(data.nodeNum - 1):
if(i != k and i != j):
expr.addTerms(big_M, Y[i][j][k])
model.addConstr(Tt[k] >= Tt[j] + data.disMatrix[j][k] + data.recoverTime - big_M + expr, "c18")
expr.clear()
# constraint (19)
for k in range(1, data.nodeNum):
for j in range(1, data.nodeNum - 1):
for i in range(data.nodeNum - 1):
if(i != j and i != k and j != k):
model.addConstr(Tt[k] - Tt[j] + data.disMatrix[i][j] <= data.range + big_M - big_M * Y[i][j][k], "c19")
# constraint (20)
for i in range(1, data.nodeNum - 1):
for j in range(1, data.nodeNum - 1):
if(i != j):
model.addConstr(U[i] - U[j] >= 1 - big_M * P[i][j], "c20")
# constraint (21)
for i in range(1, data.nodeNum - 1):
for j in range(1, data.nodeNum - 1):
if(i != j):
model.addConstr(U[i] - U[j] <= -1 +big_M - big_M * P[i][j], "c21")
# constraint (22)
for i in range(1, data.nodeNum - 1):
for j in range(1, data.nodeNum - 1):
if(i != j):
model.addConstr(P[i][j] + P[j][i] == 1, "c22")
# constraint (23)
for i in range(data.nodeNum - 1):
for k in range(1, data.nodeNum):
for l in range(1, data.nodeNum - 1):
if(k != i and l != i and l != k):
expr1 = LinExpr(0)
expr2 = LinExpr(0)
for j in range(1, data.nodeNum - 1):
if(k != j and i != j):
expr1.addTerms(big_M, Y[i][j][k])
for m in range(1, data.nodeNum - 1):
for n in range(1, data.nodeNum):
if(l != m and l != n and m != n):
expr2.addTerms(big_M, Y[l][m][n])
model.addConstr(Tt[l] >= Tt[k] - 3*big_M + expr1 + expr2 + big_M * P[i][l], "c23")
expr1.clear()
expr2.clear()
# constraint (24)
model.addConstr(T[0] == 0, "c24")
# constraint (25)
model.addConstr(Tt[0] == 0, "c25")
# constraint (26)
for j in range(1, data.nodeNum - 1):
model.addConstr(P[0][j] == 1, "c26")
# constraint (27)
for i in range(data.nodeNum):
for j in range(data.nodeNum):
if(i == j):
model.addConstr(X[i][j] == 0, "c27")
for k in range(data.nodeNum):
if(i == j or i == k or k == j):
model.addConstr(Y[i][j][k] == 0, "c28")
# solve the problem
model.write('a.lp')
model.Params.timelimit = 3600
model.optimize()
# get the solution info
solution = Solution()
solution = solution.getSolution(data, model)
print("\n\n\n\n-----optimal value-----")
print("Obj: %g" % solution.ObjVal)
print("\n\n ------Route of truck------")
# print("Truck: ", end = " ")
j = 0
for i in range(data.nodeNum):
i = j # note that the variable is whether is a local variable or a global variable
# print("i = %d, j = %d" % (i, j), end = " ")
for j in range(data.nodeNum):
if(solution.X[i][j] == 1):
print(" %d -" % i, end = " ")
# print(" i = %d, j = %d" % (i, j))
break
print(" 0")
print("\n\n ------Route of UAV ------- ")
count = 0
for i in range(data.nodeNum):
for j in range(data.nodeNum):
for k in range(data.nodeNum):
if(solution.Y[i][j][k] == 1):
count = count + 1
print("UAV %d : %d - %d - %d" % (count, i, j, k))
# draw the route graph
# draw all the nodes first
# data1 = Data()
# readData(data1, path, 100)
fig = plt.figure(figsize=(15,10))
font_dict = {'family': 'Arial', # serif
'style': 'normal', # 'italic',
'weight': 'normal',
'color': 'darkred',
'size': 30,
}
font_dict2 = {'family': 'Arial', # serif
'style': 'normal', # 'italQic',
'weight': 'normal',
'color': 'darkred',
'size': 24,
}
plt.xlabel('x', font_dict)
plt.ylabel('y', font_dict)
plt.title('Optimal Solution for FSTSP (5 customers)', font_dict)
plt.xticks(fontsize=22)
plt.yticks(fontsize=22) # plt.yticks(fontsize=30)
plt.grid(True, color='r', linestyle='-', linewidth=2)
'''
marker='o'
marker=','
marker='.'
marker=(9, 3, 30)
marker='+'
marker='v'
marker='^'
marker='<'
marker='>'
marker='1'
marker='2'
marker='3'
red blue green
'''
plt.scatter(data.cor_X[0], data.cor_Y[0], c='blue', alpha=1, marker=',', linewidths=5, label='depot')
plt.scatter(data.cor_X[1:-1], data.cor_Y[1:-1], c='magenta', alpha=1, marker='o', linewidths=5, label='customer') # c='red'定义为红色,alpha是透明度,marker是画的样式
# draw the route
for i in range(data.nodeNum):
for j in range(data.nodeNum):
if(solution.X[i][j] == 1):
x = [data.cor_X[i], data.cor_X[j]]
y = [data.cor_Y[i], data.cor_Y[j]]
plt.plot(x, y, 'b', linewidth = 3)
# plt.text(data.cor_X[i]-1, data.cor_Y[i], str(i), fontsize=15, color = 'black')
# plt.text(coverage50index*0.98, 4, coverage50index, fontsize=10, color = 'red')
plt.text(data.cor_X[i]-0.2, data.cor_Y[i], str(i), fontdict = font_dict2)
for i in range(data.nodeNum):
for j in range(data.nodeNum):
for k in range(data.nodeNum):
if(solution.Y[i][j][k] == 1):
x = [data.cor_X[i], data.cor_X[j], data.cor_X[k]]
y = [data.cor_Y[i], data.cor_Y[j], data.cor_Y[k]]
plt.plot(x, y, 'r--', linewidth = 3)
plt.text(data.cor_X[j]-0.2, data.cor_Y[j], str(j), fontdict = font_dict2)
#plt.plot(x, y, 'r--', label = "UAV", linewidth = 3)
# plt.grid(True)
plt.grid(False)
plt.legend(loc='best', fontsize = 20)
plt.show()
数值实验
算例
算例我们就采用Solomon的VRP benchmark的算例数据,只是抽出其中的一些点作为我们算例的点。
这里我们需要对Solomon benchmark的算例做一些小改动,就是设置无人机的飞行里程RANGE,以及设置无人机的发射时间和回收时间LUNCTING和RECOVER。如下图,我们设置
RANGE= 100
LUNCTING=1
RECOVER=1
其余的数据不做改动。
设置无人机的里程为100修改虽然感觉不合理,但是这样在小规模的情况下能够让无人机被发射出去服务一个顾客点。
举Solomon benchmark的c101为例,修改后的算理数据如下:
RANGE
100
LUNCTING RECOVER
1 1
CUSTOMER
CUST NO. XCOORD. YCOORD. DEMAND READY TIME DUE DATE SERVICE TIME
0 40 50 0 0 1236 0
1 45 68 10 912 967 90
2 45 70 30 825 870 90
3 42 66 10 65 146 90
4 42 68 10 727 782 90
5 42 65 10 15 67 90
6 40 69 20 621 702 90
7 40 66 20 170 225 90
8 38 68 20 255 324 90
9 38 70 10 534 605 90
10 35 66 10 357 410 90
11 35 69 10 448 505 90
12 25 85 20 652 721 90
13 22 75 30 30 92 90
14 22 85 10 567 620 90
15 20 80 40 384 429 90
16 20 85 40 475 528 90
17 18 75 20 99 148 90
18 15 75 20 179 254 90
19 15 80 10 278 345 90
20 30 50 10 10 73 90
21 30 52 20 914 965 90
22 28 52 20 812 883 90
23 28 55 10 732 777 90
24 25 50 10 65 144 90
25 25 52 40 169 224 90
26 25 55 10 622 701 90
27 23 52 10 261 316 90
28 23 55 20 546 593 90
29 20 50 10 358 405 90
30 20 55 10 449 504 90
31 10 35 20 200 237 90
32 10 40 30 31 100 90
33 8 40 40 87 158 90
34 8 45 20 751 816 90
35 5 35 10 283 344 90
36 5 45 10 665 716 90
37 2 40 20 383 434 90
38 0 40 30 479 522 90
39 0 45 20 567 624 90
40 35 30 10 264 321 90
41 35 32 10 166 235 90
42 33 32 20 68 149 90
43 33 35 10 16 80 90
44 32 30 10 359 412 90
45 30 30 10 541 600 90
46 30 32 30 448 509 90
47 30 35 10 1054 1127 90
48 28 30 10 632 693 90
49 28 35 10 1001 1066 90
50 26 32 10 815 880 90
51 25 30 10 725 786 90
52 25 35 10 912 969 90
53 44 5 20 286 347 90
54 42 10 40 186 257 90
55 42 15 10 95 158 90
56 40 5 30 385 436 90
57 40 15 40 35 87 90
58 38 5 30 471 534 90
59 38 15 10 651 740 90
60 35 5 20 562 629 90
61 50 30 10 531 610 90
62 50 35 20 262 317 90
63 50 40 50 171 218 90
64 48 30 10 632 693 90
65 48 40 10 76 129 90
66 47 35 10 826 875 90
67 47 40 10 12 77 90
68 45 30 10 734 777 90
69 45 35 10 916 969 90
70 95 30 30 387 456 90
71 95 35 20 293 360 90
72 53 30 10 450 505 90
73 92 30 10 478 551 90
74 53 35 50 353 412 90
75 45 65 20 997 1068 90
76 90 35 10 203 260 90
77 88 30 10 574 643 90
78 88 35 20 109 170 90
79 87 30 10 668 731 90
80 85 25 10 769 820 90
81 85 35 30 47 124 90
82 75 55 20 369 420 90
83 72 55 10 265 338 90
84 70 58 20 458 523 90
85 68 60 30 555 612 90
86 66 55 10 173 238 90
87 65 55 20 85 144 90
88 65 60 30 645 708 90
89 63 58 10 737 802 90
90 60 55 10 20 84 90
91 60 60 10 836 889 90
92 67 85 20 368 441 90
93 65 85 40 475 518 90
94 65 82 10 285 336 90
95 62 80 30 196 239 90
96 60 80 10 95 156 90
97 60 85 30 561 622 90
98 58 75 20 30 84 90
99 55 80 10 743 820 90
100 55 85 20 647 726 90
结果展示与可视化
由于该问题比较难求解,我们先来一个小算例。
设置nodeNum = 5
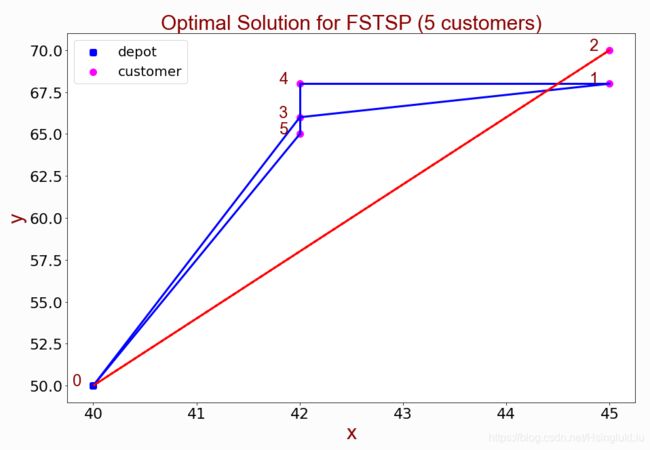
我们设置nodeNum = 5,结果为:
注意,设置有5个顾客点的时候,点
0和点6就代表depot。其余的以此类推。
Explored 3528 nodes (35235 simplex iterations) in 1.15 seconds
Thread count was 8 (of 8 available processors)
Solution count 4: 42.2311 42.2311 43.3318 47.0835
Optimal solution found (tolerance 1.00e-04)
Best objective 4.223105625185e+01, best bound 4.223105625185e+01, gap 0.0000%
['X', '0', '5'] = 1
['X', '1', '3'] = 1
['X', '3', '6'] = 1
['X', '4', '1'] = 1
['X', '5', '4'] = 1
0 - 5 - 4 - 1 - 3 - 0
------Route of UAV -------
0 5 4 1 3 0
------Route of UAV -------
UAV 0 : 0 - 2 - 6
UAV 0 : 0 - 2 - 6
UAV 0 : 0 - 2 - 6
-----optimal value-----
Obj: 42.2311
------Route of truck------
0 - 5 - 4 - 1 - 3 - 0
------Route of UAV -------
UAV 1 : 0 - 2 - 6
其中,
蓝色的路径代表卡车的路径;
红色的路径代表无人机的路径。
可以看到
- 卡车的服务顺序 0 → 5 → 4 → 1 → 3 → 0 0 \rightarrow 5 \rightarrow 4 \rightarrow 1 \rightarrow 3 \rightarrow 0 0→5→4→1→3→0
无人机服务任务为: 0 → 2 → 0 0 \rightarrow 2 \rightarrow 0 0→2→0
最终服务完所有顾客的时间为42.23。
设置nodeNum = 7
设置nodeNum = 8
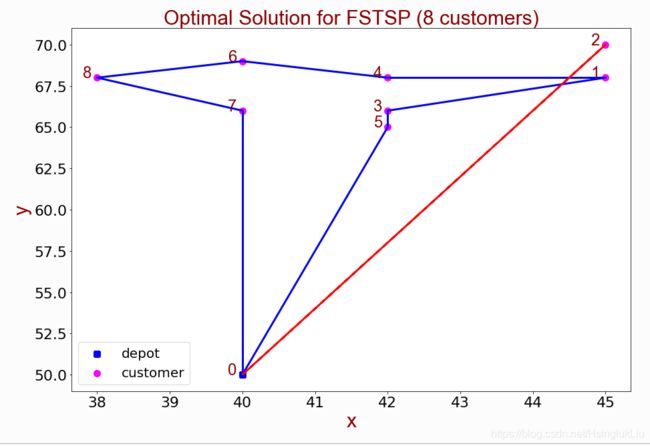
nodeNum设置成8。求解时间为4m 26s。
Explored 163568 nodes (11107937 simplex iterations) in 265.29 seconds
Thread count was 16 (of 16 available processors)
Solution count 10: 47.0389 47.0389 47.0389 ... 49.1723
Optimal solution found (tolerance 1.00e-04)
Best objective 4.703886030563e+01, best bound 4.703886030563e+01, gap 0.0000%
['X', '0', '7'] = 1
['X', '1', '3'] = 1
['X', '3', '5'] = 1
['X', '4', '1'] = 1
['X', '5', '9'] = 1
['X', '6', '4'] = 1
['X', '7', '8'] = 1
['X', '8', '6'] = 1
0 - 7 - 8 - 6 - 4 - 1 - 3 - 5 - 0
------Route of UAV -------
0 7 8 6 4 1 3 5 0
------Route of UAV -------
UAV 0 : 0 - 2 - 9
UAV 0 : 0 - 2 - 9
UAV 0 : 0 - 2 - 9
-----optimal value-----
Obj: 47.0389
------Route of truck------
0 - 7 - 8 - 6 - 4 - 1 - 3 - 5 - 0
------Route of UAV -------
UAV 1 : 0 - 2 - 9
结果为
设置nodeNum = 10
拓展
FSTSP求解起来比较难,本推文介绍的这篇,作者在论文中提出了一些启发式的求解方法。如果后续有机会,我们可以继续拓展。
当然,还有一些论文提出了动态规划的方法。见文献[2][5]。
这里我们也附上几篇其他相关文献。
关注公众号并留言获取参考文献下载链接以及测试算例。
参考文献
[1]:Murray, C. C., & Chu, A. G. (2015). The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transportation Research Part C: Emerging Technologies, 54, 86-109. https://doi.org/10.1016/j.trc.2015.03.005
[2]: Agatz N, Bouman P, Schmidt M. Optimization approaches for the traveling salesman problem with drone[J]. Transportation Science, 2018, 52(4): 965-981.
[3]:Ham A M. Integrated scheduling of m-truck, m-drone, and m-depot constrained by time-window, drop-pickup, and m-visit using constraint programming[J]. Transportation Research Part C: Emerging Technologies, 2018, 91: 1-14.
[4]:Chang Y S, Lee H J. Optimal delivery routing with wider drone-delivery areas along a shorter truck-route[J]. Expert Systems with Applications, 2018, 104: 307-317.
[5]:Bouman P, Agatz N, Schmidt M. Dynamic programming approaches for the traveling salesman problem with drone[J]. Networks, 2018, 72(4): 528-542.