强化学习:带MonteCarlo的Reinforce求解MountainCar问题

小车爬山问题

• 连续状态空间:$S=({\mathbf{x}}_t,{\mathbf{v}}_t{)}^T$,${\mathbf{x}}_{\mathbf{t}}\in [-1.2,0.6]$，${\mathbf{v}}_{\mathbf{t}}\in [-0.07,0.07]$，$x_0\in [-0.6,-0.4],v_0=0$。
• 动作空间:$A=\{0,1,2\}$,0代表全油门后退，1代码空挡，2代表全速前进。
• 奖励$r$：每个时刻的奖励均为-1。
• 模型:小车速度更新计算公式:$v_{t+1}=v_t+0.001A_t-0.0025\cos (3x_t),|v_{t+1}|\le 0.07$ .小车位置更新:$x_{t+1}=x_t+v_{t+1},-1.2\le x_{t+1}\le 0.6$。
• $\gamma =0.9$

Reinforce(MonteCarlo)算法

对于策略网络$\pi (a_t|s_t;\theta )$,其梯度计算公式为:
$${\nabla }_{\theta }J(\theta )\approx \sum _{t=1}^n{G}_t{\nabla }_{\theta }\ln \pi (a_t|s_t;\theta )$$其中$G_t$为折扣回报。参数更新为:
$$\theta \leftarrow \theta +\alpha {\nabla }_{\theta }J(\theta )$$

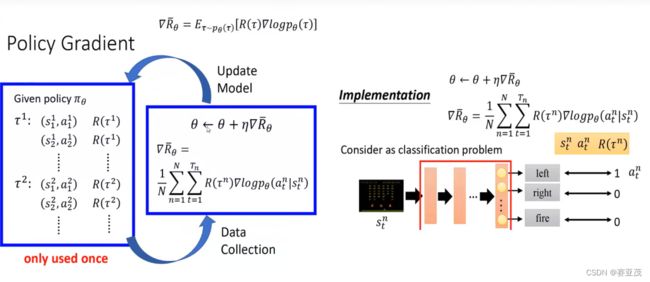
官方代码

训练代码

import torch
import gym
import numpy as np
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import matplotlib.pyplot as plt
%matplotlib inline

# avoid the gym warning message
gym.logger.set_level(40)

env = gym.make('MountainCar-v0')
env = env.unwrapped
env.seed(1)

np.random.seed(1)
torch.manual_seed(1)

state_space = env.observation_space.shape[0]
action_space = env.action_space.n
eps = np.finfo(np.float32).eps.item()


class PolicyNetwork(nn.Module):
    def __init__(self, num_inputs, num_actions, hidden_size =24, learning_rate = 0.01): 
        super (PolicyNetwork, self).__init__()
        
        self.fc1 = nn.Linear(num_inputs, hidden_size)
        self.fc2 = nn.Linear(hidden_size, num_actions)
        self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)
        
    def forward(self, state):
        x = torch.relu(self.fc1(state))
        x = F.softmax(self.fc2(x), dim=1)
        return x
        
    def choose_action(self, state):
        state = torch.from_numpy(state).float().unsqueeze(0)
        act_probs = self.forward(state)
        c = Categorical(act_probs)
        action = c.sample()
        return action.item(), c.log_prob(action)
    
    def update_policy(self, vts, log_probs): 
        policy_loss = []
        for log_prob, vt in zip (log_probs, vts):
            policy_loss.append (-log_prob * vt)
            
        self.optimizer.zero_grad()
        policy_loss = torch.stack(policy_loss).sum()
        policy_loss.backward()
        self.optimizer.step()
        
    def discounted_norm_rewards (self, rewards, GAMMA):
        vt = np.zeros_like(rewards)
        running_add = 0
        for t in reversed (range(len(rewards))):
            running_add = running_add * GAMMA + rewards[t]
            vt[t] = running_add
            
        #normalized discounted rewards
        vt = (vt - np.mean(vt)) / (np.std(vt)+eps)
        return vt


policy_net = PolicyNetwork(state_space,action_space)


def main (episodes = 5000, GAMMA = 0.99):
    all_rewards = []
    running_rewards = []
    for episode in range(episodes): 
        state = env.reset()
        rewards = []
        log_probs = []
        i = 0
        while True:
            i += 1
            action, log_prob = policy_net.choose_action(state)
            new_state, reward, done, _ = env.step(action)
            rewards.append(reward)
            log_probs.append(log_prob)

            if done: 
                vt = policy_net.discounted_norm_rewards(rewards, GAMMA)
                policy_net.update_policy(vt, log_probs)
                all_rewards.append(np.sum(rewards))
                running_rewards.append(np.mean(all_rewards[-30:]))
                print("episode={},循环{}次时的状态:{}".format(episode,i, state))
                break
            state = new_state
        print('episode:', episode, 'total reward: ', all_rewards[-1], 'running reward:', int(running_rewards[-1]))  
    return all_rewards, running_rewards, vt

all_rewards, running_rewards, vt = main(episodes = 100)
# 下面将神经网络保存
torch.save(policyNet,"policyNet.pkl")

画图代码

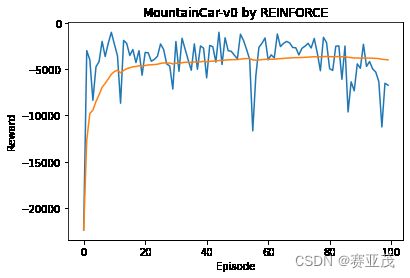
plt.plot(all_rewards)       
plt.plot(running_rewards)
plt.title('MountainCar-v0 by REINFORCE')
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.savefig(f"15.9.jpg", dpi=600)
plt.show()

我的代码

虽然和官方差不多，但是收敛速度极慢不知道为什么

import gym
import torch
import numpy as np
import torch.distributions as distributions
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import matplotlib.pyplot as plt

# 配置随机数种子且避免出现警告
gym.logger.set_level(40)
np.random.seed(1)
torch.manual_seed(1)

class policyNetwork(nn.Module):
    def __init__(self,num_inputs,num_actions,num_hidden=24,lr=0.01):
        super(policyNetwork, self).__init__()
        self.fc1 = nn.Linear(num_inputs,num_hidden)
        self.fc2 = nn.Linear(num_hidden,num_actions)
        self.optimizer = optim.Adam(self.parameters(),lr=lr)

    # 定义前馈
    def forward(self,state):
        x = torch.relu(self.fc1(state))
        x = F.softmax(self.fc2(x),dim=1) # 对输入的每一行进行softmax操作
        return x

    # 根据动作分布采样执行并且计算
    def select_action(self,state):
        # 输入:state状态
        # 输出:抽样A_t,lnpi(A_t|S_t)
        state = torch.from_numpy(state).float().unsqueeze(0)
        action_probs = self.forward(state)
        c = distributions.Categorical(action_probs)
        action = c.sample() # 按照一定概率分布采样
        return action.item(),c.log_prob(action)

    # 更新policy
    def update_policy(self,vts,log_probs):
        policy_loss = []
        for log_prob,vt in zip(log_probs,vts):
            policy_loss.append(-log_prob*vt)
        # 初始化优化器
        self.optimizer.zero_grad()
        loss = torch.stack(policy_loss).sum()
        loss.backward()
        self.optimizer.step()

    # 计算vt
    def discounted_rewards(self,rewards,gamma=1.0):
        vt = np.zeros_like(rewards)
        temp_add = 0
        for t in reversed(range(len(rewards))):
            temp_add = temp_add*gamma + rewards[t]
            vt[t] = temp_add
        # # normalized discounted rewards
        # vt = (vt - np.mean(vt)) / (np.std(vt) + 1e-7)
        return vt

    # 定义训练函数
    def train_network(self,epsiodes=5000,gamma=0.99):
        # 用来记录奖励数组
        rewards_array = []
        mean_array = []
        # 导入环境变量
        env = gym.make("MountainCar-v0")
        env = env.unwrapped
        for epsiode in range(epsiodes):
            i = 0
            state = env.reset()
            print("epsiode={}时的起始状态:{}".format(epsiode,state))
            rewards = []
            log_probs = []
            while True:
                i += 1
                action,log_prob = self.select_action(state)
                next_state,reward,done,_ = env.step(action) # 内部的state每次都会更新
                rewards.append(reward)
                log_probs.append(log_prob)

                if done:
                    rewards_array.append(np.sum(rewards))
                    vts = self.discounted_rewards(rewards,gamma=gamma)
                    self.update_policy(vts,log_probs)
                    # print("epsiode:",epsiode,'total_rewards:',rewards_array[-1])
                    print("循环{}次时的状态:{}".format(i, state))
                    break
                state = next_state
            mean_array.append(np.mean(rewards_array))
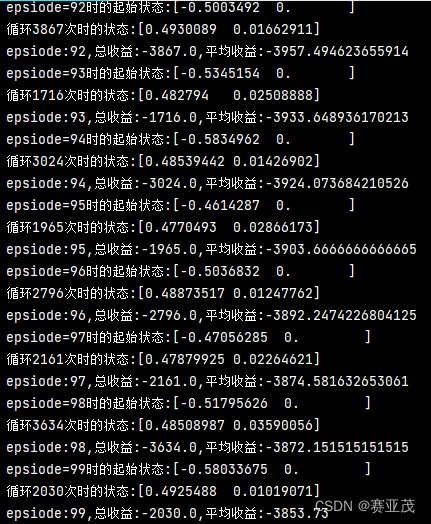
            print("epsiode:{},总收益:{},平均收益:{}".format(epsiode,rewards_array[-1],mean_array[-1]))
        return rewards_array,mean_array

if __name__ == "__main__":
    policyNet = policyNetwork(num_inputs=2, num_actions=3)
    rewards_array,mean_array = policyNet.train_network(epsiodes=100)
    # 下面将神经网络保存
    torch.save(policyNet,"policyNet.pkl")
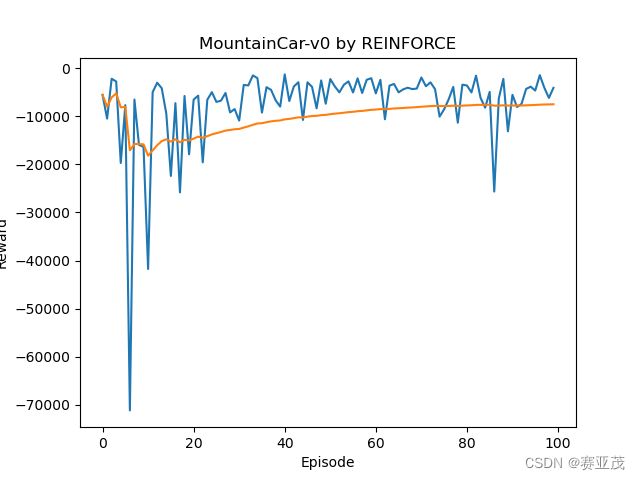
    plt.plot(rewards_array)
    plt.plot(mean_array)
    plt.title('MountainCar-v0 by REINFORCE')
    plt.xlabel('Episode')
    plt.ylabel('Reward')
    plt.savefig(f"15.9.jpg", dpi=600)
    plt.show()

下图是采用标准化折扣回报后的:

$$G_t\leftarrow \frac{(G_t-\overline{G_t})}{std(G_t)}$$

结论:对$G_t$的标准化可以显著提高收敛速度。