字符串搜索算法效率对比：BF\RK\BM\KMP\Sunday

字符串搜索算法效率对比

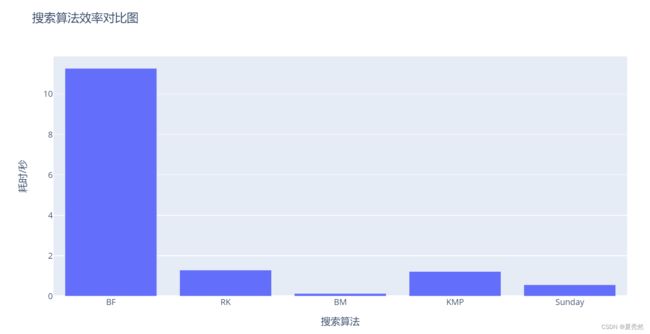
以下为 BF\RK\BM\KMP\Sunday 五种搜索算法的执行耗时对比，具体代码放下面了，感兴趣的兄弟可以看一下，有什么问题留言探讨。

一、生成数据

生成大批量数据，主串长度为610w，模式串长度为10w，且主串中对应的模式串位置为第50w个。

import random
def generate_random_str(randomlength=16):
    random_str = ''
    base_str ='abcdefghigklmnopqrstuvwxyz'
    length =len(base_str) -1
    for i in range(randomlength):
        random_str +=base_str[random.randint(0, length)]
    return random_str

needle = generate_random_str(100000)
haystack = generate_random_str(5000000) + needle + generate_random_str(1000000)

二、BF算法

思路：
记录主串为S，模式串为P。逐字符地进行匹配(比较 $S[i]$ 和 $P[j]$)，如果当前字符匹配成功( $S[i]==P[j]$ )，就匹配下一个字符($++i，++j$)，如果失配，$i$ 回溯，$j$ 置为$0$ ($i=i-j+1，j=0$)。

时间复杂度：$O(m\ast n)$，与主串和模式串的长度都正相关
空间复杂度：$O(1)$

def bf(s, p):
    s_len, p_len = len(s), len(p)
    for i in range(s_len - p_len + 1):
        if s[i:i+p_len] == p:
            return i
    return -1

三、RK算法

思路：
记录主串为S，模式串为P。对于给定主串 $S$ 与模式串 $P$，通过滚动哈希算快速筛选出与模式串 $P$ 不匹配的文本位置，然后在其余位置继续检查匹配项。

时间复杂度： $O(n)$。其中文本串 $S$ 的长度为 $n$，模式串 $P$ 的长度为 $m$。
空间复杂度： $O(1)$。

def rk(s, p):
    hash_word = {chr(x):i for i, x in enumerate(range(ord('a'), ord('z')+1))}
    s_len, p_len = len(s), len(p)
    s_sum = sum(hash_word.get(i) for i in s[:p_len])
    p_sum = sum(hash_word.get(i) for i in p)
    for i in range(s_len - p_len + 1):
        if s_sum == p_sum:
            if s[i:i+p_len] == p:
                return i
        if i != s_len - p_len:
            s_sum += hash_word.get(s[i+p_len]) - hash_word.get(s[i])
    return -1

四、BM算法

BM算法也叫做精确字符集算法，它是一种从右往左比较（后往前），同时也应用到了两种规则坏字符、好后缀规则去计算我们移动的偏移量的算法。

BM算法详解点击此处查看，里面有对代码的详细注释与拆分。

时间复杂度： $O(n/m)$，最坏 $O(m\ast n)$。
空间复杂度： $O(m)$。

def bm(s, p):
    s_len, p_len = len(s), len(p)
    bc_dict = {x:i for i, x in enumerate(p)}
    suffix, prefix = [-1] * p_len, [False] * p_len
    gs_list = [None] * p_len
    
    def move(i, p_len, suffix, prefix):
        suffix_length = p_len - 1 - i
        if suffix[suffix_length] != -1:
            return i + 1 - suffix[suffix_length]
        for k in range(suffix_length-1, 0, -1):
            if prefix[k] is True:
                return p_len - k
        return p_len

    for i in range(p_len-1):
        start = i
        suffix_length = 0
        while start >=0 and p[start] == p[p_len-1-suffix_length]:
            suffix_length += 1
            suffix[suffix_length] = start
            start -= 1
        if start < 0:
            prefix[suffix_length] = True
    now = 0
    
    while now <= s_len - p_len:
        i = p_len - 1
        while i >= 0 and s[now+i] == p[i]:
            i -= 1
        if i < 0:
            return now
        bc_move = i - bc_dict.get(s[now+i], -1)
        gs_move = 0
        if p_len - 1 - i > 0:
            if gs_list[i] is None:
                gs_list[i] = move(i, p_len, suffix, prefix)
            gs_move = gs_list[i]
        now += max(bc_move, gs_move)
    return -1

五、KMP

KMP算法是一种改进的字符串匹配算法，由 D.E.Knuth，J.H.Morris 和 V.R.Pratt 提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个 next() 函数实现，函数本身包含了模式串的局部匹配信息。

想要学习的小伙伴可以参考以下内容：

• KMP算法原理快速理解可以参考此处b站教程：KMP算法易懂版
• KMP算法详细实现流程可以参考此处：简单题学 KMP 算法
• next函数详细解析可以参考此处b站教程 ：KMP算法之求next数组代码讲解

时间复杂度： $O(n+m)$，其中 $n$ 是字符串 $\text{haystack}$ 的长度，$m$ 是字符串 $\text{needle}$ 的长度。我们至多需要遍历两字符串一次。
空间复杂度： $O(m)$，其中 $m$ 是字符串 $\text{needle}$ 的长度。我们只需要保存字符串 $\text{needle}$ 的前缀列表 $next$。

def kmp(s, p):
    s_len, p_len = len(s), len(p)
    next_lis = [-1] * p_len
    i, j = 0, -1
    while i < p_len - 1:
        if j == -1 or p[i] == p[j]:
            j += 1
            i += 1
            next_lis[i] = j
        else:
            j = next_lis[j]
    i, j = 0, 0
    while i < s_len:
        if j == -1 or s[i] == p[j]:
            j += 1
            i += 1
        else:
            j = next_lis[j]
        if j == p_len:
            return i - j
    return -1

六、Sunday

Sunday算法是Daniel M.Sunday于1990年提出的字符串模式匹配。其核心思想是：在匹配过程中，模式串发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。

Sunday算法详解点击此处查看，里面有对代码的详细注释与拆分。

时间复杂度： 最坏情况：$O(nm)$，平均情况：$O(n)$
空间复杂度： $O(s)$。为偏移表长度。

def sunday(s, p):
    s_len, p_len = len(s), len(p)
    bc_dict = {x: p_len - i for i, x in enumerate(p)}
    now = 0
    while now < s_len - p_len:
        if s[now: now+p_len] == p:
            return now
        now += bc_dict.get(s[now+p_len], p_len + 1)
    if s[now: now+p_len] == p:
        return now
    return -1

七、字符串执行耗时输出代码

以下分别对上述五个算法进行调用，并输出搜索下标以及耗时，结果都是正确的保证算法没有错误，耗时结果对比就是文章置顶的柱状图。

import time
st = time.time()
print(sunday(haystack, needle))
print("sunday：",time.time() - st)

st = time.time()
print(kmp(haystack, needle))
print("kmp：",time.time() - st)

st = time.time()
print(bm(haystack, needle))
print("bm：",time.time() - st)

st = time.time()
print(rk(haystack, needle))
print("rk：",time.time() - st)

st = time.time()
print(bf(haystack, needle))
print("bf：",time.time() - st)