扩散模型(Diffusion Model)原理与代码解析(二)
扩散模型(Diffusion Model)原理与代码解析(一)
扩散模型(Diffusion Model)原理与代码解析(二)
四、损失函数
我们已经明确了要训练 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt),那要怎么确定目标函数呢?有两个很直接的想法,一个是负对数的最大似然概率,即 − log p Θ ( X 0 ) -\log p_{Θ}(X_0) −logpΘ(X0),另一个是真实分布与预测分布的交叉熵,即 − E q ( X 0 ) log p Θ ( X 0 ) -E_{q(X_0)}\log p_{Θ}(X_0) −Eq(X0)logpΘ(X0),然而,类似于VAE,由于我们很难对噪声空间进行积分,因此直接优化 − log p Θ ( X 0 ) -\log p_{Θ}(X_0) −logpΘ(X0)或 − E q ( X 0 ) log p Θ ( X 0 ) -E_{q(X_0)}\log p_{Θ}(X_0) −Eq(X0)logpΘ(X0)是很困难的,因此我们不会直接优化它们,而是优化它们的变分上界(Variational Lower Bound) L V L B L_{VLB} LVLB, L V L B L_{VLB} LVLB的定义如下: L V L B = E q ( X 0 : T ) [ log q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) ] L_{VLB}=E_{q(X_{0:T})}\left[\log\frac{q(X_{1:T}|X_0)}{p_{\Theta}(X_{0:T})}\right] LVLB=Eq(X0:T)[logpΘ(X0:T)q(X1:T∣X0)]下面证明 L V L B L_{VLB} LVLB是 − log p Θ ( X 0 ) -\log p_{Θ}(X_0) −logpΘ(X0)和 − E q ( X 0 ) log p Θ ( X 0 ) -E_{q(X_0)}\log p_{Θ}(X_0) −Eq(X0)logpΘ(X0)的上界,即证明 L V L B ≥ − log p Θ ( X 0 ) & L V L B ≥ − E q ( X 0 ) log p Θ ( X 0 ) L_{VLB} \ge -\log p_{Θ}(X_0) \And L_{VLB} \ge -E_{q(X_0)}\log p_{Θ}(X_0) LVLB≥−logpΘ(X0)&LVLB≥−Eq(X0)logpΘ(X0): − log p Θ ( X 0 ) ≤ − log p Θ ( X 0 ) + D K L ( q ( X 1 : T ∣ X 0 ) ∣ ∣ p Θ ( X 1 : T ∣ X 0 ) ) ( K L 散 度 大 于 等 于 零 ) = − log p Θ ( X 0 ) + E X 1 : T ∼ q ( X 1 : T ∣ X 0 ) ( log q ( X 1 : T ∣ X 0 ) p Θ ( X 1 : T ∣ X 0 ) ) = − log p Θ ( X 0 ) + E X 1 : T ∼ q ( X 1 : T ∣ X 0 ) ( log q ( X 1 : T ∣ X 0 ) p Θ ( X 0 ) p Θ ( X 0 : T ) ) = − log p Θ ( X 0 ) + E X 1 : T ∼ q ( X 1 : T ∣ X 0 ) ( log q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) + log p Θ ( X 0 ) ) = E X 0 : T ∼ q ( X 0 : T ) ( log q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) ) = L V L B \begin{aligned}-\log p_{\Theta}(X_0)&\leq-\log p_{\Theta}(X_0)+D_{KL}\left(q(X_{1:T}|X_0)||p_{\Theta}(X_{1:T}|X_0)\right)(KL散度大于等于零)\\&=-\log p_{\Theta}(X_0)+E_{X_{1:T}\sim q(X_{1:T}|X_0)}\left(\log\frac{q(X_{1:T}|X_0)}{p_{\Theta}(X_{1:T}|X_0)}\right)\\&=-\log p_{\Theta}(X_0)+E_{X_{1:T}\sim q(X_{1:T}|X_0)}\left(\log\frac{q(X_{1:T}|X_0)p_{\Theta}(X_0)}{p_{\Theta}(X_{0:T})}\right)\\&=-\log p_{\Theta}(X_0)+E_{X_{1:T}\sim q(X_{1:T}|X_0)}\left(\log\frac{q(X_{1:T}|X_0)}{p_{\Theta}(X_{0:T})}+\log p_{\Theta}(X_0)\right)\\&=E_{X_{0:T}\sim q(X_{0:T})}\left(\log\frac{q(X_{1:T}|X_0)}{p_{\Theta}(X_{0:T})}\right)\\&=L_{VLB}\end{aligned} −logpΘ(X0)≤−logpΘ(X0)+DKL(q(X1:T∣X0)∣∣pΘ(X1:T∣X0))(KL散度大于等于零)=−logpΘ(X0)+EX1:T∼q(X1:T∣X0)(logpΘ(X1:T∣X0)q(X1:T∣X0))=−logpΘ(X0)+EX1:T∼q(X1:T∣X0)(logpΘ(X0:T)q(X1:T∣X0)pΘ(X0))=−logpΘ(X0)+EX1:T∼q(X1:T∣X0)(logpΘ(X0:T)q(X1:T∣X0)+logpΘ(X0))=EX0:T∼q(X0:T)(logpΘ(X0:T)q(X1:T∣X0))=LVLB
L C E = − ∫ q ( X 0 ) log p Θ ( X 0 ) d X 0 = − E q ( X 0 ) log p Θ ( X 0 ) = − E q ( X 0 ) log ( ∫ p Θ ( X 1 : T ∣ X 0 ) p Θ ( X 0 ) d X 1 : T ) = − E q ( X 0 ) log ( ∫ p Θ ( X 0 : T ) d X 1 : T ) = − E q ( X 0 ) log ( ∫ q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) q ( X 1 : T ∣ X 0 ) d X 1 : T ) = − E q ( X 0 ) log ( E q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) q ( X 1 : T ∣ X 0 ) ) ≤ − E q ( X 0 ) ( E q ( X 1 : T ∣ X 0 ) log p Θ ( X 0 : T ) q ( X 1 : T ∣ X 0 ) ) = E q ( X 0 : T ) [ log q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) ] = L V L B \begin{aligned}L_{CE}&=-\int q(X_0)\log p_{\Theta}(X_0)dX_0\\&=-E_{q(X_0)}\log p_{\Theta}(X_0)\\&=-E_{q(X_0)}\log\left(\int p_{\Theta}(X_{1:T}|X_0)p_{\Theta}(X_0)dX_{1:T}\right)\\&=-E_{q(X_0)}\log\left(\int p_{\Theta}(X_{0:T})dX_{1:T}\right)\\&=-E_{q(X_0)}\log\left(\int q(X_{1:T}|X_0)\frac{p_{\Theta}(X_{0:T})}{q(X_{1:T}|X_0)}dX_{1:T}\right)\\&=-E_{q(X_0)}\log\left(E_{q(X_{1:T}|X_0)}\frac{p_{\Theta}(X_{0:T})}{q(X_{1:T}|X_0)}\right)\\&\leq -E_{q(X_0)}\left(E_{q_({X_{1:T}|X_0})}\log\frac{p_{\Theta}(X_{0:T})}{q(X_{1:T}|X_0)}\right)\\&=E_{q(X_{0:T})}\left[\log\frac{q(X_{1:T}|X_0)}{p_{\Theta}(X_{0:T})}\right]\\&=L_{VLB}\end{aligned} LCE=−∫q(X0)logpΘ(X0)dX0=−Eq(X0)logpΘ(X0)=−Eq(X0)log(∫pΘ(X1:T∣X0)pΘ(X0)dX1:T)=−Eq(X0)log(∫pΘ(X0:T)dX1:T)=−Eq(X0)log(∫q(X1:T∣X0)q(X1:T∣X0)pΘ(X0:T)dX1:T)=−Eq(X0)log(Eq(X1:T∣X0)q(X1:T∣X0)pΘ(X0:T))≤−Eq(X0)(Eq(X1:T∣X0)logq(X1:T∣X0)pΘ(X0:T))=Eq(X0:T)[logpΘ(X0:T)q(X1:T∣X0)]=LVLB至此,证明了 L V L B L_{VLB} LVLB是 − log p Θ ( X 0 ) -\log p_{Θ}(X_0) −logpΘ(X0)和 − E q ( X 0 ) log p Θ ( X 0 ) -E_{q(X_0)}\log p_{Θ}(X_0) −Eq(X0)logpΘ(X0)的上界。
下面,对 L V L B L_{VLB} LVLB化简: L V L B = E q ( X 0 : T ) [ log q ( X 1 : T ∣ X 0 ) p Θ ( X 0 : T ) ] = E q ( X 0 : T ) [ log ∏ t = 1 T q ( X t ∣ X t − 1 ) p Θ ( X T ) ∏ t = 1 T p Θ ( X t − 1 ∣ X t ) ] = E q ( X 0 : T ) [ − log p Θ ( X T ) + ∑ t = 1 T log q ( X t ∣ X t − 1 ) p Θ ( X t − 1 ∣ X t ) ] = E q ( X 0 : T ) [ − log p Θ ( X T ) + ∑ t = 2 T log q ( X t ∣ X t − 1 ) p Θ ( X t − 1 ∣ X t ) + log q ( X 1 ∣ X 0 ) p Θ ( X 0 ∣ X 1 ) ] # ( 第 二 项 分 子 q ( X t ∣ X t − 1 = q ( X t , X t − 1 , X 0 ) q ( X t − 1 , X 0 ) = q ( X t − 1 ∣ X t , X 0 ) q ( X t ∣ X 0 ) q ( X 0 ) q ( X t − 1 , X 0 ) = q ( X t − 1 ∣ X t , X 0 ) q ( X t ∣ X 0 ) q ( X t − 1 ∣ X 0 ) ) = E q ( X 0 : T ) [ − log p Θ ( X T ) + ∑ t = 2 T log ( q ( X t − 1 ∣ X t X 0 ) p Θ ( X t − 1 ∣ X t ) ∗ q ( X t ∣ X 0 ) q ( X t − 1 ∣ X 0 ) ) + log q ( X 1 ∣ X 0 ) p Θ ( X 0 ∣ X 1 ) ] = E q ( X 0 : T ) [ − log p Θ ( X T ) + ∑ t = 2 T log q ( X t − 1 ∣ X t X 0 ) p Θ ( X t − 1 ∣ X t ) + ∑ t = 2 T log q ( X t ∣ X 0 ) q ( X t − 1 ∣ X 0 ) + log q ( X 1 ∣ X 0 ) p Θ ( X 0 ∣ X 1 ) ] = E q ( X 0 : T ) [ − log p Θ ( X T ) + ∑ t = 2 T log q ( X t − 1 ∣ X t X 0 ) p Θ ( X t − 1 ∣ X t ) + log q ( X T ∣ X 0 ) q ( X 1 ∣ X 0 ) + log q ( X 1 ∣ X 0 ) p Θ ( X 0 ∣ X 1 ) ] = E q ( X 0 : T ) [ − log p Θ ( X T ) + ∑ t = 2 T log q ( X t − 1 ∣ X t X 0 ) p Θ ( X t − 1 ∣ X t ) + log q ( X T ∣ X 0 ) p Θ ( X 0 ∣ X 1 ) ] = E q ( X 0 : T ) [ log q ( X T ∣ X 0 ) p Θ ( X T ) + ∑ t = 2 T log q ( X t − 1 ∣ X t X 0 ) p Θ ( X t − 1 ∣ X t ) − log p Θ ( X 0 ∣ X 1 ) ] = D K L ( q ( X T ∣ X 0 ) ∣ ∣ p Θ ( X T ) ) + ∑ t = 2 T D K L ( q ( X t − 1 ∣ X t X 0 ) ∣ ∣ p Θ ( X t − 1 ∣ X t ) ) − log p Θ ( X 0 ∣ X 1 ) = L T + L T − 1 + . . . + L 0 w h e r e : L T = D K L ( q ( X T ∣ X 0 ) ∣ ∣ p Θ ( X T ) ) L t = D K L ( q ( X t ∣ X t + 1 X 0 ) ∣ ∣ p Θ ( X t ∣ X t + 1 ) ) , 1 ≤ t ≤ T L 0 = − log p Θ ( X 0 ∣ X 1 ) \begin{aligned}L_{VLB}&= E_{q(X_{0:T})}\left[\log\frac{q(X_{1:T}|X_0)}{p_{Θ}(X_{0:T})}\right]\\&=E_{q(X_{0:T})}\left[\log\frac{\textstyle \prod_{t=1}^{T}q(X_{t}|X_{t-1})}{p_{Θ}(X_{T}){\textstyle \prod_{t=1}^{T}}p_{Θ}(X_{t-1}|X_t)}\right]\\&=E_{q(X_{0:T})}\left[-\log p_{Θ}(X_T)+\sum_{t=1}^{T}\log\frac{q(X_{t}|X_{t-1})}{p_{Θ}(X_{t-1}|X_t)}\right]\\&=E_{q(X_{0:T})}\left[-\log p_{Θ}(X_T)+\sum_{t=2}^{T}\log\frac{q(X_{t}|X_{t-1})}{p_{Θ}(X_{t-1}|X_t)}+\log\frac{q(X_{1}|X_{0})}{p_{Θ}(X_{0}|X_1)}\right] \#(第二项分子q(X_t|X_{t-1}=\frac{q(X_t,X_{t-1},X_0)}{q(X_{t-1},X_0)}=\frac{q(X_{t-1}|X_t,X_0)q(X_t|X_0)q(X_0)}{q(X_{t-1},X_0)}=\frac{q(X_{t-1}|X_t,X_0)q(X_t|X_0)}{q(X_{t-1}|X_0)})\\&=E_{q(X_{0:T})}\left[-\log p_{Θ}(X_T)+\sum_{t=2}^{T}\log\left(\frac{q(X_{t-1}|X_{t}X_0)}{p_{Θ}(X_{t-1}|X_t)}*\frac{q(X_{t}|X_0)}{q(X_{t-1}|X_0)}\right)+\log\frac{q(X_{1}|X_{0})}{p_{Θ}(X_{0}|X_1)}\right]\\&=E_{q(X_{0:T})}\left[-\log p_{Θ}(X_T)+\sum_{t=2}^{T}\log\frac{q(X_{t-1}|X_{t}X_0)}{p_{Θ}(X_{t-1}|X_t)}+\sum_{t=2}^{T}\log\frac{q(X_{t}|X_0)}{q(X_{t-1}|X_0)}+\log\frac{q(X_{1}|X_{0})}{p_{Θ}(X_{0}|X_1)}\right]\\&=E_{q(X_{0:T})}\left[-\log p_{Θ}(X_T)+\sum_{t=2}^{T}\log\frac{q(X_{t-1}|X_{t}X_0)}{p_{Θ}(X_{t-1}|X_t)}+\log\frac{q(X_{T}|X_0)}{q(X_{1}|X_0)}+\log\frac{q(X_{1}|X_{0})}{p_{Θ}(X_{0}|X_1)}\right]\\&=E_{q(X_{0:T})}\left[-\log p_{Θ}(X_T)+\sum_{t=2}^{T}\log\frac{q(X_{t-1}|X_{t}X_0)}{p_{Θ}(X_{t-1}|X_t)}+\log\frac{q(X_{T}|X_0)}{p_{\Theta}(X_{0}|X_1)}\right]\\&=E_{q(X_{0:T})}\left[\log\frac{q(X_T|X_0)}{p_{Θ}(X_T)} +\sum_{t=2}^{T}\log\frac{q(X_{t-1}|X_{t}X_0)}{p_{Θ}(X_{t-1}|X_t)}-\log p_{Θ}(X_{0}|X_1)\right]\\&=D_{KL}(q(X_T|X_0)||p_{Θ}(X_T))+\sum_{t=2}^{T} D_{KL}(q(X_{t-1}|X_tX_0)||p_{Θ}(X_{t-1}|X_t))-\log p_{Θ}(X_{0}|X_1)\\&= L_{T} + L_{T-1} + ...+ L_{0}\\& where: L_{T} = D_{KL}(q(X_T|X_0)||p_{Θ}(X_{T}))\\& L_{t} = D_{KL}(q(X_t|X_{t+1}X_0)||p_{Θ}(X_{t}|X_{t+1})),1 \le t \le T\\& L_{0} = -\log p_{Θ}(X_{0}|X_{1})\end{aligned} LVLB=Eq(X0:T)[logpΘ(X0:T)q(X1:T∣X0)]=Eq(X0:T)[logpΘ(XT)∏t=1TpΘ(Xt−1∣Xt)∏t=1Tq(Xt∣Xt−1)]=Eq(X0:T)[−logpΘ(XT)+t=1∑TlogpΘ(Xt−1∣Xt)q(Xt∣Xt−1)]=Eq(X0:T)[−logpΘ(XT)+t=2∑TlogpΘ(Xt−1∣Xt)q(Xt∣Xt−1)+logpΘ(X0∣X1)q(X1∣X0)]#(第二项分子q(Xt∣Xt−1=q(Xt−1,X0)q(Xt,Xt−1,X0)=q(Xt−1,X0)q(Xt−1∣Xt,X0)q(Xt∣X0)q(X0)=q(Xt−1∣X0)q(Xt−1∣Xt,X0)q(Xt∣X0))=Eq(X0:T)[−logpΘ(XT)+t=2∑Tlog(pΘ(Xt−1∣Xt)q(Xt−1∣XtX0)∗q(Xt−1∣X0)q(Xt∣X0))+logpΘ(X0∣X1)q(X1∣X0)]=Eq(X0:T)[−logpΘ(XT)+t=2∑TlogpΘ(Xt−1∣Xt)q(Xt−1∣XtX0)+t=2∑Tlogq(Xt−1∣X0)q(Xt∣X0)+logpΘ(X0∣X1)q(X1∣X0)]=Eq(X0:T)[−logpΘ(XT)+t=2∑TlogpΘ(Xt−1∣Xt)q(Xt−1∣XtX0)+logq(X1∣X0)q(XT∣X0)+logpΘ(X0∣X1)q(X1∣X0)]=Eq(X0:T)[−logpΘ(XT)+t=2∑TlogpΘ(Xt−1∣Xt)q(Xt−1∣XtX0)+logpΘ(X0∣X1)q(XT∣X0)]=Eq(X0:T)[logpΘ(XT)q(XT∣X0)+t=2∑TlogpΘ(Xt−1∣Xt)q(Xt−1∣XtX0)−logpΘ(X0∣X1)]=DKL(q(XT∣X0)∣∣pΘ(XT))+t=2∑TDKL(q(Xt−1∣XtX0)∣∣pΘ(Xt−1∣Xt))−logpΘ(X0∣X1)=LT+LT−1+...+L0where:LT=DKL(q(XT∣X0)∣∣pΘ(XT))Lt=DKL(q(Xt∣Xt+1X0)∣∣pΘ(Xt∣Xt+1)),1≤t≤TL0=−logpΘ(X0∣X1)从 L t L_{t} Lt即可看出,对 p Θ ( X t ∣ X t + 1 ) p_{Θ}(X_{t}|X_{t+1}) pΘ(Xt∣Xt+1)的监督就是最小化 p Θ ( X t ∣ X t + 1 ) p_{Θ}(X_{t}|X_{t+1}) pΘ(Xt∣Xt+1)和 q ( X t ∣ X t + 1 X 0 ) q(X_t|X_{t+1}X_0) q(Xt∣Xt+1X0)的KL散度。
简单的说,我们的目的是希望学习出一个 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt),即能够从噪声图恢复出原图。为了达到这一个目的,我们使用 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0)来监督 p Θ ( X t − 1 ∣ X t ) p_{Θ}(X_{t-1}|X_t) pΘ(Xt−1∣Xt)进行训练, q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0)是可以用 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0)和 q ( X t ∣ X t − 1 ) q(X_t|X_{t-1}) q(Xt∣Xt−1)表示的,即 q ( X t − 1 ∣ X t X 0 ) q(X_{t-1}|X_tX_0) q(Xt−1∣XtX0)是已知的。
DDPM论文将 p Θ ( X t − 1 ∣ X t ) = N ( X t − 1 ; μ θ ( X t , t ) , Σ θ ( X t , t ) ) p_{Θ}(X_{t-1}|X_t)=N(X_{t-1};\mu_{\theta}(X_t,t),\Sigma_{\theta}(X_t,t)) pΘ(Xt−1∣Xt)=N(Xt−1;μθ(Xt,t),Σθ(Xt,t))中的方差设置为 β t \beta_t βt,所以可学习的参数就只在均值中。对于两个单一变量的高斯分布 p p p和 q q q而言, K L ( p , q ) = log σ 2 σ 1 + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 − 1 2 KL(p,q)=\log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2} KL(p,q)=logσ1σ2+2σ22σ12+(μ1−μ2)2−21优化式子: ∑ t = 1 T D K L ( q ( X t − 1 ∣ X t X 0 ) ∣ ∣ p Θ ( X t − 1 ∣ X t ) ) \sum_{t=1}^{T} D_{KL}(q(X_{t-1}|X_tX_0)||p_{Θ}(X_{t-1}|X_t)) t=1∑TDKL(q(Xt−1∣XtX0)∣∣pΘ(Xt−1∣Xt))其中, q q q为已知有偏高斯分布, p Θ p_{\Theta} pΘ为所要拟合的分布,由于假设 p Θ p_{\Theta} pΘ的方差为常数,则我们只需逼近 p Θ p_{\Theta} pΘ和 q q q的均值即可,等价于最小化式子: L o s s = E q ( 1 2 σ t 2 ∣ ∣ μ ˉ t ( X t , X 0 ) − μ θ ( X t , t ) ∣ ∣ 2 ) + C # ( X t 是 由 X 0 和 噪 声 ϵ 决 定 的 变 量 ) = E X 0 , ϵ ( 1 2 σ t 2 ∣ ∣ μ ˉ t ( X t ( X 0 , ϵ ) , X 0 ) − μ θ ( X t , t ) ∣ ∣ 2 ) # ( 由 于 X t = α ˉ t X 0 + 1 − α ˉ t Z , Z ∼ N ( 0 , I ) , 即 可 求 出 X 0 的 表 达 式 ) = E X 0 , ϵ ( 1 2 σ t 2 ∣ ∣ 1 α t ( X t ( X 0 , ϵ ) − β t 1 − α ˉ t ϵ ) − μ θ ( X t , t ) ∣ ∣ 2 ) # ( 带 入 μ ˉ ( X t , X 0 ) 的 表 达 式 , 上 述 的 X 0 可 不 做 替 换 ) # 作 者 认 为 直 接 预 测 恢 复 的 数 据 效 果 不 好 , 转 而 预 测 噪 声 , 这 个 想 法 有 点 像 预 测 残 差 连 接 中 的 残 差 # 一 个 网 络 输 入 X 0 , α ˉ t , 高 斯 噪 声 ϵ 和 t , 然 后 预 测 高 斯 噪 声 ϵ = E X 0 , ϵ ( 1 2 σ t 2 ∣ ∣ 1 α t ( X t ( X 0 , ϵ ) − β t 1 − α ˉ t ϵ ) − 1 α t ( X t − β t 1 − α ˉ t ϵ θ ( X t , t ) ) ∣ ∣ 2 ) = E X 0 , ϵ ( β t 2 2 σ t 2 α t ( 1 − α ˉ t ) ∣ ∣ ϵ − ϵ θ ( α ˉ t X 0 + 1 − α ˉ t ϵ , t ) ∣ ∣ 2 ) \begin{aligned}Loss&=\mathbb{E}_q\left(\frac{1}{2\sigma_t^2}||\bar{\mu}_t(X_t,X_0)-\mu_{\theta}(X_t,t)||^2\right)+C \space\space\#(X_t是由X_0和噪声\epsilon决定的变量)\\&=\mathbb{E}_{X_0,\epsilon}\left(\frac{1}{2\sigma_t^2}||\bar{\mu}_t(X_t(X_0,\epsilon),X_0)-\mu_{\theta}(X_t,t)||^2\right)\space\space\#(由于X_t=\sqrt{\bar{\alpha}_t}X_0+\sqrt{1-\bar{\alpha}_t}Z,Z\sim N(0,I),即可求出X_0的表达式)\\&=\mathbb{E}_{X_0,\epsilon}\left(\frac{1}{2\sigma_t^2}||\frac{1}{\sqrt{\alpha_t}}(X_t(X_0,\epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon)-\mu_{\theta}(X_t,t)||^2\right)\space\space\#(带入\bar{\mu}(X_t,X_0)的表达式,上述的X_0可不做替换)\\& \#作者认为直接预测恢复的数据效果不好,转而预测噪声,这个想法有点像预测残差连接中的残差\\& \#一个网络输入X_0,\bar{\alpha}_t,高斯噪声\epsilon和t,然后预测高斯噪声\epsilon\\&=\mathbb{E}_{X_0,\epsilon}\left(\frac{1}{2\sigma_t^2}||\frac{1}{\sqrt{\alpha_t}}(X_t(X_0,\epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon)-\frac{1}{\sqrt{\alpha_t}}(X_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_{\theta}(X_t,t))||^2\right)\\&=\mathbb{E}_{X_0,\epsilon}\left(\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}||\epsilon-\epsilon_{\theta}(\sqrt{\bar{\alpha}_t}X_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t)||^2\right)\end{aligned} Loss=Eq(2σt21∣∣μˉt(Xt,X0)−μθ(Xt,t)∣∣2)+C #(Xt是由X0和噪声ϵ决定的变量)=EX0,ϵ(2σt21∣∣μˉt(Xt(X0,ϵ),X0)−μθ(Xt,t)∣∣2) #(由于Xt=αˉtX0+1−αˉtZ,Z∼N(0,I),即可求出X0的表达式)=EX0,ϵ(2σt21∣∣αt1(Xt(X0,ϵ)−1−αˉtβtϵ)−μθ(Xt,t)∣∣2) #(带入μˉ(Xt,X0)的表达式,上述的X0可不做替换)#作者认为直接预测恢复的数据效果不好,转而预测噪声,这个想法有点像预测残差连接中的残差#一个网络输入X0,αˉt,高斯噪声ϵ和t,然后预测高斯噪声ϵ=EX0,ϵ(2σt21∣∣αt1(Xt(X0,ϵ)−1−αˉtβtϵ)−αt1(Xt−1−αˉtβtϵθ(Xt,t))∣∣2)=EX0,ϵ(2σt2αt(1−αˉt)βt2∣∣ϵ−ϵθ(αˉtX0+1−αˉtϵ,t)∣∣2)作者在训练时发现,去掉Loss前的系数,可使训练稳定,所以简化后的Loss为 L o s s = E X 0 , ϵ ( ∣ ∣ ϵ − ϵ θ ( α ˉ t X 0 + 1 − α ˉ t ϵ , t ) ∣ ∣ 2 ) Loss=\mathbb{E}_{X_0,\epsilon}\left(||\epsilon-\epsilon_{\theta}(\sqrt{\bar{\alpha}_t}X_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t)||^2\right) Loss=EX0,ϵ(∣∣ϵ−ϵθ(αˉtX0+1−αˉtϵ,t)∣∣2)拟合出来的均值为 μ θ ( x t , t ) = 1 α t ( X t − β t 1 − α ˉ t ϵ θ ( X t , t ) ) \mu_{\theta}(x_t,t)=\frac{1}{\sqrt{\alpha_t}}\left(X_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_{\theta}(X_t,t)\right) μθ(xt,t)=αt1(Xt−1−αˉtβtϵθ(Xt,t))可用于采样。
五、训练和采样过程
训练过程:从数据集中采样 x 0 x_0 x0,从均匀分布采样 t t t,可使模型鲁棒,采样噪声,计算 Loss 更新模型。
采样过程:从标准正态分布采样 x T x_T xT,迭代计算 x t − 1 x_{t-1} xt−1,已知均值 μ θ ( x t , t ) \mu_\theta(x_t,t) μθ(xt,t)和常数方差 β t \beta_t βt利用参数重整化可计算出 x t − 1 x_{t-1} xt−1,直到 x 0 x_0 x0。
六、Pytorch示例代码
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_moons
import torch
import torch.nn as nn
from PIL import Image
moons_curve, _ = make_moons(10 ** 4, noise=0.05)
print("shape of moons:", np.shape(moons_curve))
data = moons_curve.T
fig, ax = plt.subplots()
ax.scatter(*data, color='blue', edgecolor='white')
ax.axis('off')
dataset = torch.Tensor(moons_curve).float()
num_steps = 100 # 扩散100步
# 制定每一步的beta
betas = torch.linspace(-6, 6, num_steps)
betas = torch.sigmoid(betas) * (0.5e-2 - 1e-5) + 1e-5 # 先压缩到0~1,再乘以0.005
# 计算alpha、alpha_prod、alpha_prod_previous、alpha_bar_sqrt等变量的值
alphas = 1 - betas
alphas_prod = torch.cumprod(alphas, 0)
alphas_prod_p = torch.cat([torch.tensor([1]).float(), alphas_prod[:-1]], 0) # 插入第一个数1,丢掉最后一个数,previous连乘
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)
assert alphas.shape == alphas_prod.shape == alphas_prod_p.shape == alphas_bar_sqrt.shape == one_minus_alphas_bar_log.shape == one_minus_alphas_bar_sqrt.shape
print("all the same shape", betas.shape) # 所有值都是同等维度,且都是常值
# 计算任意时刻的x采样值,基于X_0和重参数化 , 扩散过程
def q_x(X_0, t):
noise = torch.randn_like(X_0)
alphas_t = alphas_bar_sqrt[t]
alphas_1_m_t = one_minus_alphas_bar_sqrt[t]
return (alphas_t * X_0 + alphas_1_m_t * noise) # 在X_0的基础上添加噪声
num_shows = 20
fig, axs = plt.subplots(2, 10, figsize=(28, 3))
plt.rc('text', color='black')
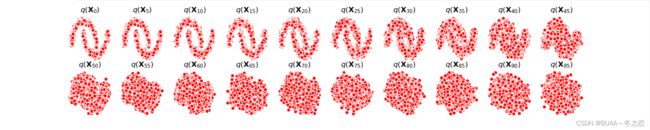
# 共有10000个点,每个点包含两个坐标。生成100步中每隔5步加噪声后的图像,最终应该会成为一个各向同性的高斯分布
for i in range(num_shows):
j = i // 10
k = i % 10
q_i = q_x(dataset, torch.tensor([i * num_steps // num_shows])) # 生成t时刻的采样数据
axs[j, k].scatter(q_i[:, 0], q_i[:, 1], color='red', edgecolor='white')
axs[j, k].set_axis_off()
axs[j, k].set_title('$q(\mathbf{X}_{' + str(i * num_steps // num_shows) + '})$')
fig.show()
class MLPDiffusion(nn.Module): # 定义一个 MLP 模型
def __init__(self, n_steps, num_units=128):
super(MLPDiffusion, self).__init__()
self.linears = nn.ModuleList(
[
nn.Linear(2, num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, 2),
]
)
self.step_embeddings = nn.ModuleList(
[
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units),
]
)
def forward(self, x, t):
# x = x_0
for idx, embedding_layer in enumerate(self.step_embeddings): # 三层
t_embedding = embedding_layer(t)
x = self.linears[2 * idx](x)
x += t_embedding
x = self.linears[2 * idx + 1](x)
x = self.linears[-1](x) # 输出维度与输入一致
return x
def diffusion_loss_fn(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):
"""对任意时刻t进行采样计算loss"""
batch_size = x_0.shape[0]
# 对一个batchsize样本生成随机的时刻t
t = torch.randint(0, n_steps, size=(batch_size // 2,)) # 为了 t 不重复,先采样一半
t = torch.cat([t, n_steps - 1 - t], dim=0)
t = t.unsqueeze(-1)
# x0的系数
a = alphas_bar_sqrt[t]
# 随机噪声eps的系数
aml = one_minus_alphas_bar_sqrt[t]
# 生成随机噪音eps
e = torch.randn_like(x_0)
# 构造模型的输入
x = x_0 * a + e * aml
# 送入模型,得到t时刻的随机噪声预测值
output = model(x, t.squeeze(-1))
# 与真实噪声一起计算误差,求平均值
return (e - output).square().mean()
def p_sample_loop(model, shape, n_steps, betas, one_minus_alphas_bar_sqrt):
"""从x[T]恢复x[T-1]、x[T-2]|...x[0]"""
cur_x = torch.randn(shape)
x_seq = [cur_x]
for i in reversed(range(n_steps)):
cur_x = p_sample(model, cur_x, i, betas, one_minus_alphas_bar_sqrt)
x_seq.append(cur_x)
return x_seq
def p_sample(model, x, t, betas, one_minus_alphas_bar_sqrt):
"""从 x_t 开始生成 t-1 时刻的重构值"""
t = torch.tensor([t])
coeff = betas[t] / one_minus_alphas_bar_sqrt[t]
eps_theta = model(x, t)
mean = (1 / (1 - betas[t]).sqrt()) * (x - (coeff * eps_theta))
z = torch.randn_like(x)
sigma_t = betas[t].sqrt()
sample = mean + sigma_t * z
return (sample)
# 开始训练模型
seed = 1234
print('Training model...')
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
num_epoch = 4001
plt.rc('text', color='blue')
model = MLPDiffusion(num_steps) # 输出维度是2,输入是x和step
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
for t in range(num_epoch):
for idx, batch_x in enumerate(dataloader):
loss = diffusion_loss_fn(model, batch_x, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, num_steps)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.) # 梯度裁剪
optimizer.step()
if (t % 100 == 0):
print(loss)
x_seq = p_sample_loop(model, dataset.shape, num_steps, betas, one_minus_alphas_bar_sqrt)
fig, axs = plt.subplots(1, 10, figsize=(28, 3))
for i in range(1, 11):
cur_x = x_seq[i * 10].detach()
axs[i - 1].scatter(cur_x[:, 0], cur_x[:, 1], color='red', edgecolor='white');
axs[i - 1].set_axis_off();
axs[i - 1].set_title('$q(\mathbf{x}_{' + str(i * 10) + '})$')
fig.show()
第0个epoch,100次扩散,每10次输出一次

第1000个epoch:

第2000个epoch:

第3000个epoch:

# 生成扩散和逆扩散的 GIF
imgs = []
for i in range(100):
plt.clf()
q_i = q_x(dataset,torch.tensor([i]))
plt.scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white',s=5);
plt.axis('off');
img_buf = io.BytesIO()
plt.savefig(img_buf,format='png')
img = Image.open(img_buf)
imgs.append(img)
reverse = []
for i in range(100):
plt.clf()
cur_x = x_seq[i].detach()
plt.scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white',s=5);
plt.axis('off')
img_buf = io.BytesIO()
plt.savefig(img_buf,format='png')
img = Image.open(img_buf)
reverse.append(img)
imgs = imgs + reverse
imgs[0].save("diffusion.gif", format='GIF', append_images=imgs, save_all=True, duration=100, loop=0)