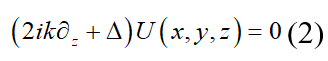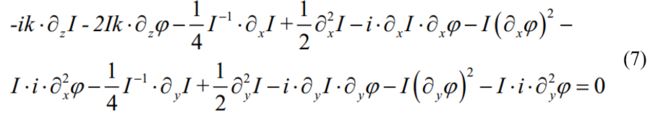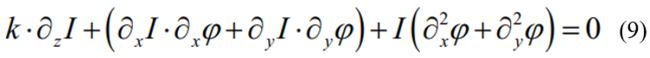基于强度传输方程法相位恢复技术实例演示
一、引言
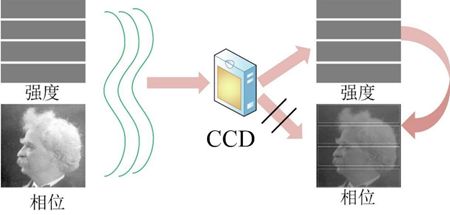
CCD相机无法直接记录相位分布。因此，如何通过测量的强度信息来恢复相位信息，即对相位恢复技术的研究尤为重要。
目前，基于强度传输方程(Transport of Intensity Equation, TIE)的相位恢复技术已广泛应用于三维重建、光学显微成像、全息技术、衍射光学和光学测量等众多领域，解决了这些领域的许多研究问题。
二、强度传输方程的推导
假设一束单色光沿着z轴自由传播，其复振幅的表示形式可以写为
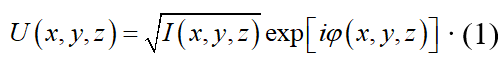
其中， U ( x , y , z ) U\left( x,y,z \right) U(x,y,z)为光场复振幅， I ( x , y , z ) I\left( x,y,z \right) I(x,y,z)为光场强度， φ ( x , y , z ) \varphi \left( x,y,z \right) φ(x,y,z)为光场相位。那么在傍轴近似的条件下，光场的传播满足下面抛物线方程：
其中 ∂ z = ∂ / ∂ z {{\partial }_{z}}={\partial }/{\partial z}\; ∂z=∂/∂z代表沿z方向的强度分布的变化量，
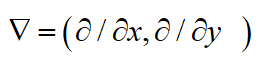
表示梯度算子
表示二维拉普拉斯算子，k为波数，与波长λ之间满足k=2π/λ。分别对 U ( x , y , z ) U\left( x,y,z \right) U(x,y,z) 在(x,y,z)方向上求一维偏导数;
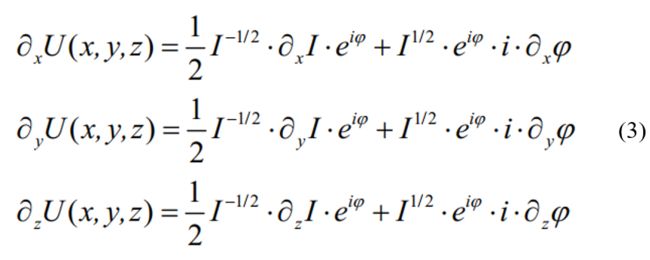
分别对 U ( x , y , z ) U\left( x,y,z \right) U(x,y,z)在x,y方向上求二维偏导数;
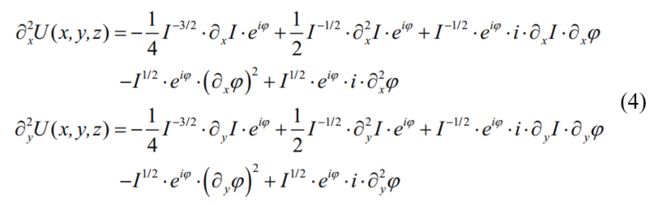
先求 U ( x , y , z ) U\left( x,y,z \right) U(x,y,z)的共轭函数 U ∗ ( x , y , z ) {{U}^{*}}\left( x,y,z \right) U∗(x,y,z)
用 U ∗ ( x , y , z ) {{U}^{*}}\left( x,y,z \right) U∗(x,y,z)左乘公式(2)得
用 U ( x , y , z ) U\left( x,y,z \right) U(x,y,z)左乘公式(4)
用式(6)减去式(7)得：
化简可得：
将式(9)进一步化简整理得：
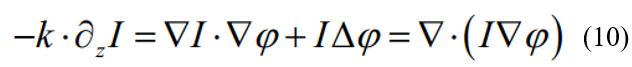
公式(10)即是推导出的强度传输方程，该方程指出，明确了强度分布以及光轴方向上的强度微分两项重要信息以后，接下来就可以对于二阶偏微分方程进行求解，最终可以得到位置z具体的平面相位分布信息。一般来说，可以采用两个或者两个以上的散焦图像，通过有限差分的方式来对于轴向微分进行预测。
三、强度传输方程的求解
关于强度传输方程的求解，较常用到有傅里叶解法、多重网格方法、格林函数方法以及把扩展成多项式方法等。我们主要介绍的是如何采用傅里叶来进行推导，这种方法可以运用在两种情况下，一种是光波场强度分布均匀的情况，还有一种是非均匀情况。
当强度分布均匀的时候，即I等于常数时，可以通过傅里叶变换有效求解强度传输方程，公式(10)简化为：
公式(11)是一个泊松方程，可以利用傅里叶变换求解两次泊松方程得到相位[2]:
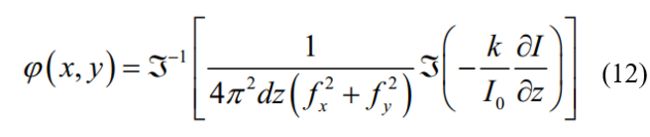
当待测光波场强度分布不均匀时，Paganin 等将傅里叶求解方法进行了拓展，其通过将辅助函数引入方程求解过程中，这样再求解公式（11）得到的相位如下：
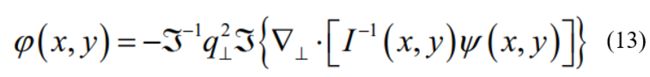
其中
f x {{f}_{x}} fx和 f y {{f}_{y}} fy表示频率域坐标。
公式（12）和式（13）中都有强度轴向微分 ∂ I / ∂ z {\partial I}/{\partial z}\; ∂I/∂z 这一项，通常情况下强度轴向微分都是用有限差分法近似得到：
式中z0为传播距离， I ( x , y , z 0 + Δ z ) I\left( x,y,{{z}_{0}}+\Delta z \right) I(x,y,z0+Δz)和 I ( x , y , z 0 − Δ z ) I\left( x,y,{{z}_{0}}-\Delta z \right) I(x,y,z0−Δz)分别为记录面 z 0 + Δ z {{z}_{0}}+\Delta z z0+Δz和 z 0 − Δ z {{z}_{0}}-\Delta z z0−Δz距离处的强度分布， Δ z \Delta z Δz为距离步长。
这种简洁有效的求解方案让强度传输方程可以运用在许多领域中，这种利用傅里叶变换来实现的求解方案也成为了运用最多的一种数值解法。
四、仿真模拟分析
模拟仿真原理如下图所示：
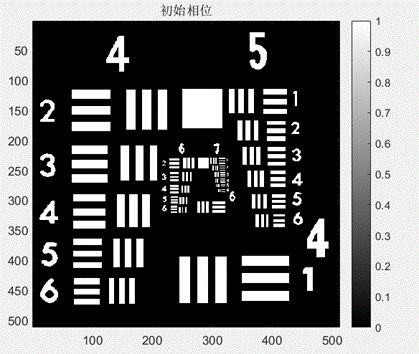
图3给出了一个仿真的初始相位
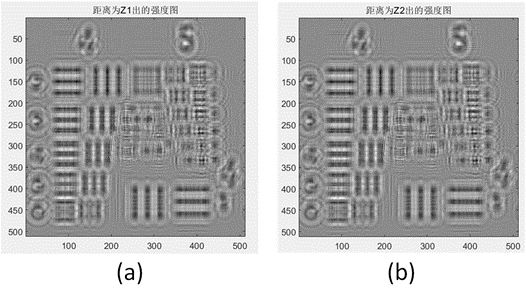
在距离z1和z2处拍摄了两幅图像，分别如图4(a)(b)所示：
两幅图像强度差如下图所示：
图6给出基于强度的相位恢复的相位图
五、资源获取
上述资源可从以下链接处获取：
https://download.csdn.net/download/qq_36584460/84989831
资源包含以下内容：
1) imlin.m
2) mypropagation.m
3) 基于强度传输方程法相位恢复技术实例演示.m
4) 基于强度传输方程法相位恢复技术实例演示-GBK格式.m(防中文注释乱码)
5) 分辨率板.bmp(模拟被测物体)
6) 原理图.png
参考文献
[1] 王金成. 基于强度传输方程的层析重建研究[D]: 安徽大学, 2020.
[2] 吴海燕. 非干涉光场的相位恢复算法研究[D]: 安徽大学, 2012.
如有疑问，可私信交流！简单光学技术组可提供相关技术支持！