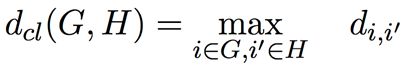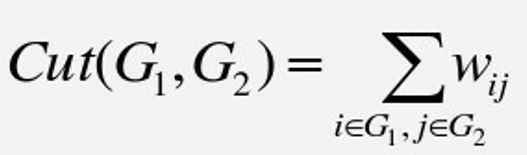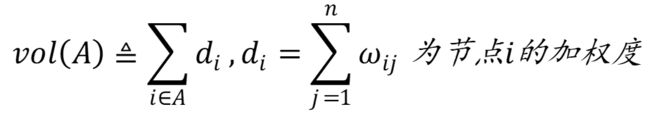数据科学/机器学习python——聚类模型【K-means聚类举例】

聚类模型

• 无标签、无监督学习
• 可以简化数据，有助于寻找数据的内部结构
• 基于相似度【能把不同领域的数据相似度的度量融合进去，还可加入核函数】；基于特征【可以直接考虑原始的数据，避免因为度量距离而丢失某些信息】
• 平坦聚类/分割聚类【直接将样本分割为多个不相交的子集】、层次聚类【通过构造具有层级的树形结构，在不同层次上对样本进行分割】

• K-means聚类

  • 起源于信号处理，是一种应用较广泛的聚类分析方法，目标是将n个样本划分到K个簇重，其中每个样本属于距离自己最近的簇【找到每个簇的中心，并最小化所有样本点到质心c_k的距离平方和】
  • 其中，r_ik∈{0,1}，用来指示样本x_i是否在簇k中，若r_ik=1，则在，对于j≠k，有r_ij=0，有
  • 
  • 过程
    • 随机选择K个样本作为初始质心
      • 重复迭代：
        • 把每个样本指派到最近的质心，形成K个簇；
        • 重新计算每个簇的质心
        • 直到质心不再变化
  • K值的选择【簇的个数】
    • 最大化模型选择，贝叶斯信息准则（BIC）n是样本个数，p是模型M中参数的个数，LL(X|M)是数据集X基于模型M的对数似然函数
    • 从K=1即一个簇开始尝试，不断对簇进行划分，直至属于每个簇的样本均服从高斯分布【不一定】
  • 质心的选择
    • 随机初始化【容易陷入局部最优，不能得到最优的聚类结果】
    • 为解决局部最优问题：多次运行，每次选取一组不同的随机初始质心，接着选取具有最小目标函数值的簇集；使用层次聚类对样本聚类，从层次聚类中提取K个簇，并选择这些簇的中心作为初始质心【有效，需要的样本数不大】
  • 优点：实现简单、直观
  • 缺点：聚类结果依赖于事先指定的K值，K个初始质心的选择；容易陷入局部最优，不易处理非簇状数据；聚类结果易受离群值影响
  • 时间复杂度：O(lnk*m)
    • l：特征维度；n：样本数量；k：簇数量；m：迭代次数
    • 在每一步迭代中，每个样本需要与k个簇中心进行距离计算
  • 变种
    • K-medoids聚类
      • 改进K-means易受离群值影响的问题
      • 选取每个簇中到簇内其他点的距离和最小的样本作为簇的质心【而非均值】，是原始数据集中的某个点
    • 二分K-means聚类
      • 每次从所有簇中选择具有最大J值得簇，然后划分为两个簇，重复该过程，直至簇集合中含有K个簇
      • 在每一次划分过程中都对质心做多次选取，选择最优得划分
      • 不能保证可以得到全局最优解
    • K-medians聚类：使用样本每个维度的中位数作为簇的质心
    • K-means++聚类：在初始化质心的过程中，选择相互距离尽可能远的样本作为初始质心
    • 基于粗糙集的K-means聚类：一个样本可以被划分给多个簇

• 层次聚类

  • 根据层次分解是以自底向上（合并、聚合）还是自顶向下（分裂、分拆）方式，都以样本两两之间的距离（距离矩阵）为输入，均是启发式的策略，并没有去优化一个明确的目标函数来实现聚类，因此也很难严格评价聚类效果
  • 局限性：一旦分裂、合并执行，就不能修正
  • 聚合式
    • 在开始时每个样本都是一个簇，每一次迭代中，将最相似的（距离（曼哈顿距离）最近）的两个簇进行合并，直到所有粗合并为包含所有样本的一个簇
    • 选择最相似的两簇的时间复杂度为O(n²)，有n步，故总算法复杂度为O(n³)，采用优先队列将复杂度降为O(n²ln(n))
    • 对于样本量很大的数据集，可以先进行K-means聚类，再对得到的簇进行层次聚类
    • 计算两簇之间的距离，计算方式不同可能会导致聚类结果不同
      • 单连接：最近邻距离，即簇G与H之间的距离定为两簇之间最近的成员间距离【没有考虑其他簇内其他成员的距离，可能违背紧致性特征（簇内成员尽可能相似）】
      • 完整连接：最远邻距离，簇G与H之间的距离定为两簇之间最远成员之间的距离【倾向于生成紧致簇】
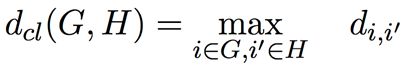
      • 平均连接：两簇间所有成员对的平均距离【易生成相对紧致的簇，同时簇间距离较远】
      • 单连接和完全连接代表了簇间距离度量的两个极端，对离群值或噪声数据过分敏感；平均连接折中，可以克服离群点敏感性问题
  • 分拆式
    • 递归将现有的簇分拆成两个子簇，n个样本的簇分拆成两个簇的可能性为2^n-1-1
    • 二分K-means聚类：选择半径最大的一簇，对该簇进行K-means聚类分为两个子簇，重复此过程直到达到想要的簇个数
    • 最小生成树法：将每个样本看作一个图节点，将样本间距离看作节点间边的权重，根据此图建立最小生成树；从权重最大处将该簇分拆为两簇
    • 距离分析法：开始的簇包含全部样本，计算样本i∈G对于所有其他样本i’∈G的平均距离从G中移除平均距离最大的样本i*，将其归为新簇H：
    • 为了同时考虑选择移动样本和H中样本的距离较小，样本选择原则可以为(停止条件为括号内为负）：
  • 层次聚类算法没有一个明确的全局目标函数来实现聚类，聚类过程由不同层次的局部规则逐步实现的，它一次性地得到了整个聚类过程，想要分多少个簇都可以直接根据树图来得到结果，改变簇的数目不需要再次计算数据点的归属类别
  • 不存在K-means聚类中选取初始质心和陷入局部最优问题，同时层次聚类能产生不同层级的聚类结果，通常更加灵活
  • 缺点：计算量大，空间、时间复杂度高于K-means聚类，而且错分在层次聚类中不可修正，一旦分错，则该样本永远停留在该聚类中

• 谱聚类

  • 一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从图割的角度来解决聚类问题，基本思路：建立一个带权重的无向图G=(V,E)，其中V的每个节点代表一个样本，E的每条边代表两个样本之间的距离，构成权重矩阵W
  • 图的划分：将图完全划分为若干个子图，各子图无交集；要求：同子图相似度高，不同子图相似度低
  • 损失函数：划分时子图之间被“截断”的边的权重和
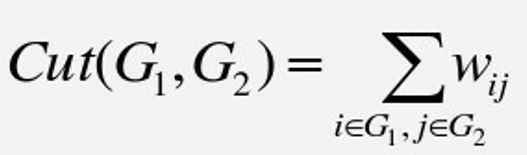
    • 最小化目标函数
  • 归一化分割（normalized cut）：
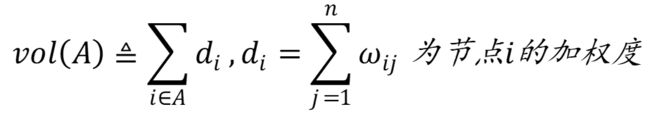
  • Laplacian矩阵
    • 
    • L为半正定矩阵(所有特征值非负)，最小特征值为0，且对应的特征向量为单位向量[1 1…1]^T
    • 损失函数：图划分问题转化为求q^TLq条件最小值问题
    • Minimum Cut方法
      • 
      • 性质：R(L,q)的最小值、次小值…最大值分别在q为L的最小特征值、次小特征值…最大特征值对应的特征向量时取得【求L次小特征值所对应的特征向量】

#1.读取数据：
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
from sklearn import preprocessing
# Importing the dataset
dataset = pd.read_csv('auto-mpg.csv', engine = 'python')

#2.数据预处理：
X = dataset.iloc[:,:-2].values
X = pd.DataFrame(X)
X = X.convert_objects(convert_numeric=True)
X.columns = ["mpg","cylinders","displacement","horsepower","weight","acceleration","model year"]

# Eliminating null values
for i in X.columns:
    X[i] = X[i].fillna(int(X[i].mean()))
for i in X.columns:
    print(X[i].isnull().sum())
#Z-Score标准化
X_zscore = pd.DataFrame(preprocessing.scale(X),\
                                   columns = X.columns)
#3.选取n_clusters：
# Using the elbow method to find  the optimal number of clusters
wcss = []
for i in range(1,11):
    kmeans = KMeans(n_clusters=i)
    kmeans.fit(X_zscore)
    wcss.append(kmeans.inertia_)
plt.plot(range(1,11),wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()

#4.K-means聚类：
# Applying k-means to the cars dataset
kmeans = KMeans(n_clusters=3) 
y_kmeans = kmeans.fit_predict(X_zscore)
X1 = X_zscore.as_matrix(columns=None)
centers = pd.DataFrame(kmeans.cluster_centers_, \
                       columns = X_zscore.columns)
centers_t = centers.T
centers_t.columns = ["cluster_0","cluster_1","cluster_2"]
print('--------------cluster_0--------------')
print(centers_t["cluster_0"].sort_values(ascending = False, inplace = False).head(10))
print('--------------cluster_1--------------')
print(centers_t["cluster_1"].sort_values(ascending = False, inplace = False).head(10))
print('--------------cluster_2--------------')
print(centers_t["cluster_2"].sort_values(ascending = False, inplace = False).head(10))
#5.数据可视化：
# Visualising the clusters
#plt.scatter(x = X_zscore.iloc[:,0], y = X_zscore.iloc[:,1], s=50, cmap='rainbow')
plt.scatter(X1[y_kmeans == 0, 0], X1[y_kmeans == 0,1],s=50,c='red')
plt.scatter(X1[y_kmeans == 1, 0], X1[y_kmeans == 1,1],s=50,c='green')
plt.scatter(X1[y_kmeans == 2, 0], X1[y_kmeans == 2,1],s=50,c='blue')
#plt.scatter(X1[y_kmeans == 3, 0], X1[y_kmeans == 3,1],s=50,c='c')
plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],marker = '*',s=100,c='yellow',label='Centroids')
plt.show()

color = ['r','g','b','c','y','m','k']
ax = plt.subplot(111,projection ='3d')
for i in range(398):
    mark = int(y_kmeans[i])
    ax.scatter(X1[i,0],X1[i,1],X1[i,2],c=color[mark])
for i in range(3):
ax.scatter(kmeans.cluster_centers_[i,0],kmeans.cluster_centers_[i,1],kmeans.cluster_centers_[i,2],c='y',marker='*',s=200)
elev =15
azim =60
ax.view_init(elev, azim)
plt.legend()
plt.show()