神经网络流程图用什么画,神经网络识别流程图解

1、如何通过人工神经网络实现图像识别

人工神经网络（Artificial Neural Networks）（简称ANN）系统从20 世纪40 年代末诞生至今仅短短半个多世纪，但由于他具有信息的分布存储、并行处理以及自学习能力等优点，已经在信息处理、模式识别、智能控制及系统建模等领域得到越来越广泛的应用。尤其是基于误差反向传播（Error Back Propagation）算法的多层前馈网络（Multiple-Layer Feedforward Network）(简称BP 网络)，可以以任意精度逼近任意的连续函数，所以广泛应用于非线性建模、函数逼近、模式分类等方面。

目标识别是模式识别领域的一项传统的课题，这是因为目标识别不是一个孤立的问题，而是模式识别领域中大多数课题都会遇到的基本问题，并且在不同的课题中，由于具体的条件不同，解决的方法也不尽相同，因而目标识别的研究仍具有理论和实践意义。这里讨论的是将要识别的目标物体用成像头(红外或可见光等)摄入后形成的图像信号序列送入计算机，用神经网络识别图像的问题。

一、BP 神经网络

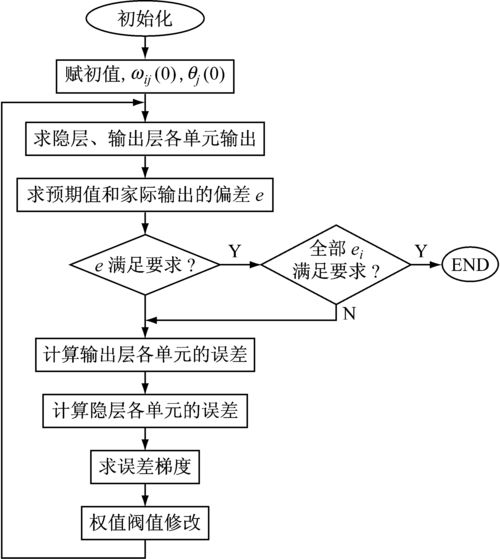
BP 网络是采用Widrow-Hoff 学习算法和非线性可微转移函数的多层网络。一个典型的BP 网络采用的是梯度下降算法，也就是Widrow-Hoff 算法所规定的。backpropagation 就是指的为非线性多层网络计算梯度的方法。一个典型的BP 网络结构如图所示。

我们将它用向量图表示如下图所示。

其中：对于第k 个模式对，输出层单元的j 的加权输入为

该单元的实际输出为

而隐含层单元i 的加权输入为

该单元的实际输出为

函数f 为可微分递减函数

其算法描述如下：

（1）初始化网络及学习参数，如设置网络初始权矩阵、学习因子等。

（2）提供训练模式，训练网络，直到满足学习要求。

（3）前向传播过程：对给定训练模式输入，计算网络的输出模式，并与期望模式比较，若有误差，则执行（4）；否则，返回（2）。

（4）后向传播过程：a. 计算同一层单元的误差；b. 修正权值和阈值；c. 返回（2）

二、 BP 网络隐层个数的选择

对于含有一个隐层的三层BP 网络可以实现输入到输出的任何非线性映射。增加网络隐层数可以降低误差，提高精度，但同时也使网络复杂化，增加网络的训练时间。误差精度的提高也可以通过增加隐层结点数来实现。一般情况下，应优先考虑增加隐含层的结点数。

三、隐含层神经元个数的选择

当用神经网络实现网络映射时，隐含层神经元个数直接影响着神经网络的学习能力和归纳能力。隐含层神经元数目较少时，网络每次学习的时间较短，但有可能因为学习不足导致网络无法记住全部学习内容；隐含层神经元数目较大时，学习能力增强，网络每次学习的时间较长，网络的存储容量随之变大，导致网络对未知输入的归纳能力下降，因为对隐含层神经元个数的选择尚无理论上的指导，一般凭经验确定。

四、神经网络图像识别系统

人工神经网络方法实现模式识别，可处理一些环境信息十分复杂，背景知识不清楚，推理规则不明确的问题，允许样品有较大的缺损、畸变，神经网络方法的缺点是其模型在不断丰富完善中，目前能识别的模式类还不够多，神经网络方法允许样品有较大的缺损和畸变，其运行速度快，自适应性能好，具有较高的分辨率。

神经网络的图像识别系统是神经网络模式识别系统的一种，原理是一致的。一般神经网络图像识别系统由预处理，特征提取和神经网络分类器组成。预处理就是将原始数据中的无用信息删除，平滑，二值化和进行幅度归一化等。神经网络图像识别系统中的特征提取部分不一定存在，这样就分为两大类：① 有特征提取部分的：这一类系统实际上是传统方法与神经网络方法技术的结合，这种方法可以充分利用人的经验来获取模式特征以及神经网络分类能力来识别目标图像。特征提取必须能反应整个图像的特征。但它的抗干扰能力不如第2类。② 无特征提取部分的：省去特征抽取，整副图像直接作为神经网络的输入，这种方式下，系统的神经网络结构的复杂度大大增加了，输入模式维数的增加导致了网络规模的庞大。此外，神经网络结构需要完全自己消除模式变形的影响。但是网络的抗干扰性能好，识别率高。

当BP 网用于分类时，首先要选择各类的样本进行训练，每类样本的个数要近似相等。其原因在于一方面防止训练后网络对样本多的类别响应过于敏感，而对样本数少的类别不敏感。另一方面可以大幅度提高训练速度，避免网络陷入局部最小点。

由于BP 网络不具有不变识别的能力，所以要使网络对模式的平移、旋转、伸缩具有不变性，要尽可能选择各种可能情况的样本。例如要选择不同姿态、不同方位、不同角度、不同背景等有代表性的样本，这样可以保证网络有较高的识别率。

构造神经网络分类器首先要选择适当的网络结构：神经网络分类器的输入就是图像的特征向量；神经网络分类器的输出节点应该是类别数。隐层数要选好，每层神经元数要合适，目前有很多采用一层隐层的网络结构。然后要选择适当的学习算法，这样才会有很好的识别效果。在学习阶段应该用大量的样本进行训练学习，通过样本的大量学习对神经网络的各层网络的连接权值进行修正，使其对样本有正确的识别结果，这就像人记数字一样，网络中的神经元就像是人脑细胞，权值的改变就像是人脑细胞的相互作用的改变，神经网络在样本学习中就像人记数字一样，学习样本时的网络权值调整就相当于人记住各个数字的形象，网络权值就是网络记住的内容，网络学习阶段就像人由不认识数字到认识数字反复学习过程是一样的。神经网络是按整个特征向量的整体来记忆图像的，只要大多数特征符合曾学习过的样本就可识别为同一类别，所以当样本存在较大噪声时神经网络分类器仍可正确识别。在图像识别阶段，只要将图像的点阵向量作为神经网络分类器的输入，经过网络的计算，分类器的输出就是识别结果。

五、仿真实验

1、实验对象

本实验用MATLAB 完成了对神经网络的训练和图像识别模拟。从实验数据库中选择0～9 这十个数字的BMP 格式的目标图像。图像大小为16×8 像素，每个目标图像分别加10％、20％、30％、40％、50％大小的随机噪声，共产生60 个图像样本。将样本分为两个部分，一部分用于训练，另一部分用于测试。实验中用于训练的样本为40个，用于测试的样本为20 个。随机噪声调用函数randn(m,n)产生。

2、网络结构

本试验采用三层的BP 网络，输入层神经元个数等于样本图像的象素个数16×8 个。隐含层选24 个神经元，这是在试验中试出的较理想的隐层结点数。输出层神经元个数就是要识别的模式数目，此例中有10 个模式，所以输出层神经元选择10 个，10 个神经元与10 个模式一一对应。

3、基于MATLAB 语言的网络训练与仿真

建立并初始化网络

% ================
S1 = 24;% 隐层神经元数目S1 选为24
[R,Q] = size(numdata);
[S2,Q] = size(targets);
F = numdata;
P=double(F);
net = newff(minmax(P),[S1 S2],{'logsig'
'logsig'},'traingda','learngdm')

这里numdata 为训练样本矩阵，大小为128×40， targets 为对应的目标输出矩阵，大小为10×40。

newff(PR,[S1 S2…SN],{TF1 TF2…TFN}，BTF,BLF,PF)为MATLAB 函数库中建立一个N 层

前向BP 网络的函数，函数的自变量PR 表示网络输入矢量取值范围的矩阵[Pmin max];S1~SN 为各层神经元的个数；TF1~TFN 用于指定各层神经元的传递函数；BTF 用于指定网络的训练函数；BLF 用于指定权值和阀值的学习函数；PF 用于指定网络的性能函数，缺省值为‘mse’。

设置训练参数

net.performFcn = 'sse'; %平方和误差
性能函数
net.trainParam.goal = 0.1; %平方和误
差目标
net.trainParam.show = 20; %进程显示
频率
net.trainParam.epochs = 5000;%最大训
练步数
net.trainParam.mc = 0.95; %动量常数
网络训练
net=init(net);%初始化网络
[net,tr] = train(net,P,T);％网络训练
对训练好的网络进行仿真
D=sim(net,P);
A = sim(net,B);

B 为测试样本向量集,128×20 的点阵。D 为网络对训练样本的识别结果，A 为测试样本的网络识别结果。实验结果表明：网络对训练样本和对测试样本的识别率均为100％。如图为64579五个数字添加50%随机噪声后网络的识别结果。

六、总结

从上述的试验中已经可以看出，采用神经网络识别是切实可行的，给出的例子只是简单的数字识别实验，要想在网络模式下识别复杂的目标图像则需要降低网络规模，增加识别能力，原理是一样的。

2、神经网络BP模型

一、BP模型概述

误差逆传播(Error Back-Propagation)神经网络模型简称为BP(Back-Propagation)网络模型神经网络识别流程图。

Pall Werbas博士于1974年在他的博士论文中提出了误差逆传播学习算法。完整提出并被广泛接受误差逆传播学习算法的是以Rumelhart和McCelland为首的科学家小组。他们在1986年出版“Parallel Distributed Processing，Explorations in the Microstructure of Cognition”(《并行分布信息处理》)一书中，对误差逆传播学习算法进行了详尽的分析与介绍，并对这一算法的潜在能力进行了深入探讨。

BP网络是一种具有3层或3层以上的阶层型神经网络。上、下层之间各神经元实现全连接，即下层的每一个神经元与上层的每一个神经元都实现权连接，而每一层各神经元之间无连接。网络按有教师示教的方式进行学习，当一对学习模式提供给网络后，神经元的激活值从输入层经各隐含层向输出层传播，在输出层的各神经元获得网络的输入响应。在这之后，按减小期望输出与实际输出的误差的方向，从输入层经各隐含层逐层修正各连接权，最后回到输入层，故得名“误差逆传播学习算法”。随着这种误差逆传播修正的不断进行，网络对输入模式响应的正确率也不断提高。

BP网络主要应用于以下几个方面：

1)函数逼近：用输入模式与相应的期望输出模式学习一个网络逼近一个函数；

2)模式识别：用一个特定的期望输出模式将它与输入模式联系起来；

3)分类：把输入模式以所定义的合适方式进行分类；

4)数据压缩：减少输出矢量的维数以便于传输或存储。

在人工神经网络的实际应用中，80%～90%的人工神经网络模型采用BP网络或它的变化形式，它也是前向网络的核心部分，体现了人工神经网络最精华的部分。

二、BP模型原理

下面以三层BP网络为例，说明学习和应用的原理。

1.数据定义

P对学习模式(xp，dp)，p=1，2，…，P；

输入模式矩阵X[N][P]=(x1，x2，…，xP)；

目标模式矩阵d[M][P]=(d1，d2，…，dP)。

三层BP网络结构

输入层神经元节点数S0=N，i=1，2，…，S0；

隐含层神经元节点数S1，j=1，2，…，S1；

神经元激活函数f1[S1]；

权值矩阵W1[S1][S0]；

偏差向量b1[S1]。

输出层神经元节点数S2=M，k=1，2，…，S2；

神经元激活函数f2[S2]；

权值矩阵W2[S2][S1]；

偏差向量b2[S2]。

学习参数

目标误差ϵ；

初始权更新值Δ0；

最大权更新值Δmax；

权更新值增大倍数η+；

权更新值减小倍数η-。

2.误差函数定义

对第p个输入模式的误差的计算公式为

中国矿产资源评价新技术与评价新模型

y2kp为BP网的计算输出。

3.BP网络学习公式推导

BP网络学习公式推导的指导思想是，对网络的权值W、偏差b修正，使误差函数沿负梯度方向下降，直到网络输出误差精度达到目标精度要求，学习结束。

各层输出计算公式

输入层

y0i=xi，i=1，2，…，S0；

隐含层

中国矿产资源评价新技术与评价新模型

y1j=f1(z1j)，

j=1，2，…，S1；

输出层

中国矿产资源评价新技术与评价新模型

y2k=f2(z2k)，

k=1，2，…，S2。

输出节点的误差公式

中国矿产资源评价新技术与评价新模型

对输出层节点的梯度公式推导

中国矿产资源评价新技术与评价新模型

E是多个y2m的函数，但只有一个y2k与wkj有关，各y2m间相互独立。

其中

中国矿产资源评价新技术与评价新模型

则

中国矿产资源评价新技术与评价新模型

设输出层节点误差为

δ2k=(dk-y2k)·f2′(z2k)，

则

中国矿产资源评价新技术与评价新模型

同理可得

中国矿产资源评价新技术与评价新模型

对隐含层节点的梯度公式推导

中国矿产资源评价新技术与评价新模型

E是多个y2k的函数，针对某一个w1ji，对应一个y1j，它与所有的y2k有关。因此，上式只存在对k的求和，其中

中国矿产资源评价新技术与评价新模型

则

中国矿产资源评价新技术与评价新模型

设隐含层节点误差为

中国矿产资源评价新技术与评价新模型

则

中国矿产资源评价新技术与评价新模型

同理可得

中国矿产资源评价新技术与评价新模型

4.采用弹性BP算法(RPROP)计算权值W、偏差b的修正值ΔW，Δb

1993年德国 Martin Riedmiller和Heinrich Braun 在他们的论文“A Direct Adaptive Method for Faster Backpropagation Learning：The RPROP Algorithm”中，提出Resilient Backpropagation算法——弹性BP算法(RPROP)。这种方法试图消除梯度的大小对权步的有害影响，因此，只有梯度的符号被认为表示权更新的方向。

权改变的大小仅仅由权专门的“更新值”

确定

中国矿产资源评价新技术与评价新模型

其中

表示在模式集的所有模式(批学习)上求和的梯度信息，(t)表示t时刻或第t次学习。

权更新遵循规则：如果导数是正(增加误差)，这个权由它的更新值减少。如果导数是负，更新值增加。

中国矿产资源评价新技术与评价新模型

RPROP算法是根据局部梯度信息实现权步的直接修改。对于每个权，我们引入它的

各自的更新值

，它独自确定权更新值的大小。这是基于符号相关的自适应过程，它基

于在误差函数E上的局部梯度信息，按照以下的学习规则更新

中国矿产资源评价新技术与评价新模型

其中0＜η-＜1＜η+。

在每个时刻，如果目标函数的梯度改变它的符号，它表示最后的更新太大，更新值

应由权更新值减小倍数因子η-得到减少；如果目标函数的梯度保持它的符号，更新值应由权更新值增大倍数因子η+得到增大。

为了减少自由地可调参数的数目，增大倍数因子η+和减小倍数因子η–被设置到固定值

η+=1.2，

η-=0.5，

这两个值在大量的实践中得到了很好的效果。

RPROP算法采用了两个参数：初始权更新值Δ0和最大权更新值Δmax

当学习开始时，所有的更新值被设置为初始值Δ0，因为它直接确定了前面权步的大小，它应该按照权自身的初值进行选择，例如，Δ0=0.1(默认设置)。

为了使权不至于变得太大，设置最大权更新值限制Δmax，默认上界设置为

Δmax=50.0。

在很多实验中，发现通过设置最大权更新值Δmax到相当小的值，例如

Δmax=1.0。

我们可能达到误差减小的平滑性能。

5.计算修正权值W、偏差b

第t次学习，权值W、偏差b的的修正公式

W(t)=W(t-1)+ΔW(t)，

b(t)=b(t-1)+Δb(t)，

其中，t为学习次数。

6.BP网络学习成功结束条件每次学习累积误差平方和

中国矿产资源评价新技术与评价新模型

每次学习平均误差

中国矿产资源评价新技术与评价新模型

当平均误差MSE＜ε，BP网络学习成功结束。

7.BP网络应用预测

在应用BP网络时，提供网络输入给输入层，应用给定的BP网络及BP网络学习得到的权值W、偏差b，网络输入经过从输入层经各隐含层向输出层的“顺传播”过程，计算出BP网的预测输出。

8.神经元激活函数f

线性函数

f(x)=x，

f′(x)=1，

f(x)的输入范围(-∞，+∞)，输出范围(-∞，+∞)。

一般用于输出层，可使网络输出任何值。

S型函数S(x)

中国矿产资源评价新技术与评价新模型

f(x)的输入范围(-∞，+∞)，输出范围(0，1)。

f′(x)=f(x)[1-f(x)]，

f′(x)的输入范围(-∞，+∞)，输出范围(0，

]。

一般用于隐含层，可使范围(-∞，+∞)的输入，变成(0，1)的网络输出，对较大的输入，放大系数较小；而对较小的输入，放大系数较大，所以可用来处理和逼近非线性的输入/输出关系。

在用于模式识别时，可用于输出层，产生逼近于0或1的二值输出。

双曲正切S型函数

中国矿产资源评价新技术与评价新模型

f(x)的输入范围(-∞，+∞)，输出范围(-1，1)。

f′(x)=1-f(x)·f(x)，

f′(x)的输入范围(-∞，+∞)，输出范围(0，1]。

一般用于隐含层，可使范围(-∞，+∞)的输入，变成(-1，1)的网络输出，对较大的输入，放大系数较小；而对较小的输入，放大系数较大，所以可用来处理和逼近非线性的输入/输出关系。

阶梯函数

类型1

中国矿产资源评价新技术与评价新模型

f(x)的输入范围(-∞，+∞)，输出范围{0，1}。

f′(x)=0。

类型2

中国矿产资源评价新技术与评价新模型

f(x)的输入范围(-∞，+∞)，输出范围{-1，1}。

f′(x)=0。

斜坡函数

类型1

中国矿产资源评价新技术与评价新模型

f(x)的输入范围(-∞，+∞)，输出范围[0，1]。

中国矿产资源评价新技术与评价新模型

f′(x)的输入范围(-∞，+∞)，输出范围{0，1}。

类型2

中国矿产资源评价新技术与评价新模型

f(x)的输入范围(-∞，+∞)，输出范围[-1，1]。

中国矿产资源评价新技术与评价新模型

f′(x)的输入范围(-∞，+∞)，输出范围{0，1}。

三、总体算法

1.三层BP网络(含输入层，隐含层，输出层)权值W、偏差b初始化总体算法

(1)输入参数X[N][P]，S0，S1，f1[S1]，S2，f2[S2]；

(2)计算输入模式X[N][P]各个变量的最大值，最小值矩阵 Xmax[N]，Xmin[N]；

(3)隐含层的权值W1，偏差b1初始化。

情形1：隐含层激活函数f( )都是双曲正切S型函数

1)计算输入模式X[N][P]的每个变量的范围向量Xrng[N]；

2)计算输入模式X的每个变量的范围均值向量Xmid[N]；

3)计算W，b的幅度因子Wmag；

4)产生[-1，1]之间均匀分布的S0×1维随机数矩阵Rand[S1]；

5)产生均值为0，方差为1的正态分布的S1×S0维随机数矩阵Randnr[S1][S0]，随机数范围大致在[-1，1]；

6)计算W[S1][S0]，b[S1]；

7)计算隐含层的初始化权值W1[S1][S0]；

8)计算隐含层的初始化偏差b1[S1]；

9))输出W1[S1][S0]，b1[S1]。

情形2：隐含层激活函数f( )都是S型函数

1)计算输入模式X[N][P]的每个变量的范围向量Xrng[N]；

2)计算输入模式X的每个变量的范围均值向量Xmid[N]；

3)计算W，b的幅度因子Wmag；

4)产生[-1，1]之间均匀分布的S0×1维随机数矩阵Rand[S1]；

5)产生均值为0，方差为1的正态分布的S1×S0维随机数矩阵Randnr[S1][S0]，随机数范围大致在[-1，1]；

6)计算W[S1][S0]，b[S1]；

7)计算隐含层的初始化权值W1[S1][S0]；

8)计算隐含层的初始化偏差b1[S1]；

9)输出W1[S1][S0]，b1[S1]。

情形3：隐含层激活函数f( )为其他函数的情形

1)计算输入模式X[N][P]的每个变量的范围向量Xrng[N]；

2)计算输入模式X的每个变量的范围均值向量Xmid[N]；

3)计算W，b的幅度因子Wmag；

4)产生[-1，1]之间均匀分布的S0×1维随机数矩阵Rand[S1]；

5)产生均值为0，方差为1的正态分布的S1×S0维随机数矩阵Randnr[S1][S0]，随机数范围大致在[-1，1]；

6)计算W[S1][S0]，b[S1]；

7)计算隐含层的初始化权值W1[S1][S0]；

8)计算隐含层的初始化偏差b1[S1]；

9)输出W1[S1][S0]，b1[S1]。

(4)输出层的权值W2，偏差b2初始化

1)产生[-1，1]之间均匀分布的S2×S1维随机数矩阵W2[S2][S1]；

2)产生[-1，1]之间均匀分布的S2×1维随机数矩阵b2[S2]；

3)输出W2[S2][S1]，b2[S2]。

2.应用弹性BP算法(RPROP)学习三层BP网络(含输入层，隐含层，输出层)权值W、偏差b总体算法

函数：Train3BP_RPROP(S0，X，P，S1，W1，b1，f1，S2，W2，b2，f2，d，TP)

(1)输入参数

P对模式(xp，dp)，p=1，2，…，P；

三层BP网络结构；

学习参数。

(2)学习初始化

1)

；

2)各层W，b的梯度值

，

初始化为零矩阵。

(3)由输入模式X求第一次学习各层输出y0，y1，y2及第一次学习平均误差MSE

(4)进入学习循环

epoch=1

(5)判断每次学习误差是否达到目标误差要求

如果MSE＜ϵ，

则，跳出epoch循环，

转到(12)。

(6)保存第epoch-1次学习产生的各层W，b的梯度值

，

(7)求第epoch次学习各层W，b的梯度值

，

1)求各层误差反向传播值δ；

2)求第p次各层W，b的梯度值

，

；

3)求p=1，2，…，P次模式产生的W，b的梯度值

，

的累加。

(8)如果epoch=1，则将第epoch-1次学习的各层W，b的梯度值

，

设为第epoch次学习产生的各层W，b的梯度值

，

。

(9)求各层W，b的更新

1)求权更新值Δij更新；

2)求W，b的权更新值

，

；

3)求第epoch次学习修正后的各层W，b。

(10)用修正后各层W、b，由X求第epoch次学习各层输出y0，y1，y2及第epoch次学习误差MSE

(11)epoch=epoch+1，

如果epoch≤MAX_EPOCH，转到(5)；

否则，转到(12)。

(12)输出处理

1)如果MSE＜ε，

则学习达到目标误差要求，输出W1，b1，W2，b2。

2)如果MSE≥ε，

则学习没有达到目标误差要求，再次学习。

(13)结束

3.三层BP网络(含输入层，隐含层，输出层)预测总体算法

首先应用Train3lBP_RPROP( )学习三层BP网络(含输入层，隐含层，输出层)权值W、偏差b，然后应用三层BP网络(含输入层，隐含层，输出层)预测。

函数：Simu3lBP( )。

1)输入参数：

P个需预测的输入数据向量xp，p=1，2，…，P；

三层BP网络结构；

学习得到的各层权值W、偏差b。

2)计算P个需预测的输入数据向量xp(p=1，2，…，P)的网络输出 y2[S2][P]，输出预测结果y2[S2][P]。

四、总体算法流程图

BP网络总体算法流程图见附图2。

五、数据流图

BP网数据流图见附图1。

六、实例

实例一 全国铜矿化探异常数据BP 模型分类

1.全国铜矿化探异常数据准备

在全国铜矿化探数据上用稳健统计学方法选取铜异常下限值33.1，生成全国铜矿化探异常数据。

2.模型数据准备

根据全国铜矿化探异常数据，选取7类33个矿点的化探数据作为模型数据。这7类分别是岩浆岩型铜矿、斑岩型铜矿、矽卡岩型、海相火山型铜矿、陆相火山型铜矿、受变质型铜矿、海相沉积型铜矿，另添加了一类没有铜异常的模型(表8-1)。

3.测试数据准备

全国化探数据作为测试数据集。

4.BP网络结构

隐层数2，输入层到输出层向量维数分别为14，9、5、1。学习率设置为0.9，系统误差1e-5。没有动量项。

表8-1 模型数据表

续表

5.计算结果图

如图8-2、图8-3。

图8-2

图8-3 全国铜矿矿床类型BP模型分类示意图

实例二 全国金矿矿石量品位数据BP 模型分类

1.模型数据准备

根据全国金矿储量品位数据，选取4类34个矿床数据作为模型数据，这4类分别是绿岩型金矿、与中酸性浸入岩有关的热液型金矿、微细浸染型型金矿、火山热液型金矿(表8-2)。

2.测试数据准备

模型样本点和部分金矿点金属量、矿石量、品位数据作为测试数据集。

3.BP网络结构

输入层为三维，隐层1层，隐层为三维，输出层为四维，学习率设置为0.8，系统误差1e-4，迭代次数5000。

表8-2 模型数据

4.计算结果

结果见表8-3、8-4。

表8-3 训练学习结果

表8-4 预测结果(部分)

续表

3、神经网络Kohonen模型

一、Kohonen模型概述

1981年芬兰赫尔辛基大学Kohonen教授提出了一个比较完整的，分类性能较好的自组织特征影射(Self-Organizing Feature Map)人工神经网络(简称SOM网络)方案。这种网络也称为Kohonen特征影射网络。

这种网络模拟大脑神经系统自组织特征影射功能，它是一种竞争式学习网络，在学习中能无监督地进行自组织学习。

二、Hohonen模型原理

1.概述

SOM网络由输入层和竞争层组成。输入层神经元数为N，竞争层由M=R×C神经元组成，构成一个二维平面阵列或一个一维阵列(R=1)。输入层和竞争层之间实现全互连接。

SOM网络的基本思想是网络竞争层各神经元竞争对输入模式的响应机会，最后仅有一个神经元成为竞争的胜者，并对那些与获胜神经元有关的各连接权朝着更有利于它竞争的方向调整，这一获胜神经元就表示对输入模式的分类。

SOM算法是一种无教师示教的聚类方法，它能将任意输入模式在输出层映射成一维或二维离散图形，并保持其拓扑结构不变。即在无教师的情况下，通过对输入模式的自组织学习，在竞争层将分类结果表示出来。此外，网络通过对输入模式的反复学习，可以使连接权矢量空间分布密度与输入模式的概率分布趋于一致，即连接权矢量空间分布能反映输入模式的统计特征。

2.网络权值初始化

因为网络输入很可能出现在中间区，因此，如果竞争层的初始权值选择在输入空间的中间区，则其学习效果会更加有效。

3.邻域距离矩阵

SOM网络中的神经元可以按任何方式排列，这种排列可以用表示同一层神经元间的Manhattan距离的邻域距离矩阵D来描述，而两神经元的Manhattan距离是指神经元坐标相减后的矢量中，其元素绝对值之和。

4.Kohonen竞争学习规则

设SOM网络的输入模式为Xp=(

，

，…，

)，p=1，2.…，P。竞争层神经元的输出值为Yj(j=1，2，…，M)，竞争层神经元j与输入层神经元之间的连接权矢量为

Wj=(wj1，wj2，…，wjN)，j=1，2，…，M。

Kohonen网络自组织学习过程包括两个部分：一是选择最佳匹配神经元，二是权矢量自适应变化的更新过程。

确定输入模式Xp与连接权矢量Wj的最佳匹配的评价函数是两个矢量的欧氏距离最小，即

，j=1，2，…，M，]]

g，确定获胜神经元g。

dg=mjin(dj)，j=1，2，…，M。

求输入模式Xp在竞争层的获胜神经元g及其在邻域距离nd内的神经元的输出。

中国矿产资源评价新技术与评价新模型

dgm为邻域距离矩阵D的元素，为竞争层中获胜神经元g与竞争层中其它神经元的距离。

求输入模式Xp在竞争层的获胜神经元g及其在邻域距离nd内的神经元的权值修正值。

中国矿产资源评价新技术与评价新模型

式中：i=1，2，…，N；

lr为学习速率；

t为学习循环次数。

Δwjt(t+1)的其余元素赋值为0。

进行连接权的调整

wji(t+1)=wji(t)+Δwji(t+1)。

5.权值学习中学习速率及邻域距离的更新

(1)SOM网络的学习过程分为两个阶段

第一阶段为粗学习与粗调整阶段。在这一阶段内，连接权矢量朝着输入模式的方向进行调整，神经元的权值按照期望的方向在适应神经元位置的输入空间建立次序，大致确定输入模式在竞争层中所对应的影射位置。一旦各输入模式在竞争层有了相对的影射位置后，则转入精学习与细调整阶段，即第二阶段。在这一阶段内，网络学习集中在对较小的范围内的连接权进行调整，神经元的权值按照期望的方向在输入空间伸展，直到保留到他们在粗调整阶段所建立的拓扑次序。

学习速率应随着学习的进行不断减小。

(2)邻域的作用与更新

在SOM网络中，脑神经细胞接受外界信息的刺激产生兴奋与抑制的变化规律是通过邻域的作用来体现的邻域规定了与获胜神经元g连接的权向量Wg进行同样调整的其他神经元的范围。在学习的最初阶段，邻域的范围较大，随着学习的深入进行，邻域的范围逐渐缩小。

(3)学习速率及邻域距离的更新

在粗调整阶段，

学习参数初始化

最大学习循环次数 MAX_STEP1=1000，

粗调整阶段学习速率初值 LR1=1.4，

细调整阶段学习速率初值 LR2=0.02，

最大邻域距离 MAX_ND1=Dmax，

Dmax为邻域距离矩阵D的最大元素值。

粗调阶段

学习循环次数step≤MAX_STEP1，

学习速率lr从LR1调整到LR2，

邻域距离nd 从MAX_ND1调整到1，

求更新系数r，

r=1-step/MAX_STEP1，

邻域距离nd更新，

nd=1.00001+(MAX_ND1-1)×r。

学习速率lr更新，

lr=LR2+(LR1-LR2)×r。

在细调整阶段，

学习参数初始化，

最大学习循环次数 MAX_STEP2=2000，

学习速率初值 LR2=0.02，

最大邻域距离 MAX_ND2=1。

细调阶段

MAX_STEP1＜step≤MAX_STEP1+MAX_STEP2，

学习速率lr慢慢从LR2减少，

邻域距离nd设为1，

邻域距离nd更新，

nd=MAX_ND2+0.00001。

学习速率lr更新，

lr=LR2×(MAX_STEP1/step)。

6.网络的回想——预测

SOM网络经学习后按照下式进行回想：

中国矿产资源评价新技术与评价新模型

Yj=0，j=1，2，…，M，(j≠g)。

将需要分类的输入模式提供给网络的输入层，按照上述方法寻找出竞争层中连接权矢量与输入模式最接近的神经元，此时神经元有最大的激活值1，而其它神经元被抑制而取0值。这时神经元的状态即表示对输入模式的分类。

三、总体算法

1.SOM权值学习总体算法

(1)输入参数X[N][P]。

(2)构造权值矩阵W[M][N]。

1)由X[N][P]求Xmid[N]，

2)由Xmid[N]构造权值W[M][N]。

(3)构造竞争层。

1)求竞争层神经元数M，

2)求邻域距离矩阵D[M][M]，

3)求矩阵D[M][M]元素的最大值Dmax。

(4)学习参数初始化。

(5)学习权值W[M][N]。

1)学习参数学习速率lr，邻域距离nd更新，分两阶段：

(i)粗调阶段更新；

(ii)细调阶段更新。

2)求输入模式X[N][p]在竞争层的获胜神经元win[p]。

(i)求X[N][p]与W[m][N]的欧氏距离dm；

(ii)按距离dm最短，求输入模式X[N][p]在竞争层的获胜神经元win[p]。

3)求输入模式X[N][p]在竞争层的获胜神经元win[p]及其在邻域距离nd内的神经元的输出Y[m][p]。

4)求输入模式X[N][p]在竞争层的获胜神经元win[p]及其

在邻域距离nd内的神经元的权值修正值ΔW[m][N]，

从而得到输入模式X[N][p]产生的权值修正值ΔW[M][N]。

5)权值修正W[M][N]=W[M][N]+ΔW[M][N]。

6)学习结束条件：

(i)学习循环到MAX_STEP次；

(ii)学习速率lr达到用户指定的LR_MIN；

(iii)学习时间time达到用户指定的TIME_LIM。

(6)输出。

1)学习得到的权值矩阵W[M][N]；

2)邻域距离矩阵D[M][M]。

(7)结束。

2.SOM预测总体算法

(1)输入需分类数据X[N][P]，邻域距离矩阵D[M][M]。

(2)求输入模式X[N][p]在竞争层的获胜神经元win[p]。

1)求X[N][p]与W[m][N]的欧氏距离dm；

2)按距离dm最短，求输入模式X[N][p]在竞争层的获胜神经元win[p]。

(3)求获胜神经元win[p]在竞争层排列的行列位置。

(4)输出与输入数据适应的获胜神经元win[p]在竞争层排列的行列位置，作为分类结果。

(5)结束。

四、总体算法流程图

Kohonen总体算法流程图见附图4。

五、数据流图

Kohonen数据流图见附图4。

六、无模式识别总体算法

假定有N个样品，每个样品测量M个变量，则有原始数据矩阵：

X=(xij)N×M，i=1，2，…，N，j=1，2，…，M。

(1)原始数据预处理

X=(xij)N×M处理为Z=(zij)N×M，

分3种处理方法：

1)衬度；

2)标准化；

3)归一化。

程序默认用归一化处理。

(2)构造Kohonen网

竞争层与输入层之间的神经元的连接权值构成矩阵WQ×M。

WQ×M初始化。

(3)进入Kohonen网学习分类循环，用epoch记录循环次数，epoch=1。

(4)在每个epoch循环中，对每个样品n(n=1，2，…，N)进行分类。从1个样品n=1开始。

(5)首先计算输入层的样品n的输入数据znm(m=1，2，…，M)与竞争层Q个神经元对应权值wqm的距离。

(6)寻找输入层的样品n与竞争层Q个神经元的最小距离，距离最小的神经元Win[n]为获胜神经元，将样品n归入获胜神经元Win[n]所代表的类型中，从而实现对样品n的分类。

(7)对样品集中的每一个样品进行分类：

n=n+1。

(如果n≤N，转到5。否则，转到8。)

(8)求分类后各神经元所对应的样品的变量的重心，用对应的样品的变量的中位数作为重心，用对应的样品的变量的重心来更新各神经元的连接权值。

(9)epoch=epoch+1；

一次学习分类循环结束。

(10)如果满足下列两个条件之一，分类循环结束，转到11；

否则，分类循环继续进行，转到4。

1)全部样品都固定在某个神经元上，不再改变了；

2)学习分类循环达到最大迭代次数。

(11)输出：

1)N个样品共分成多少类，每类多少样品，记录每类的样品编号；

2)如果某类中样品个数超过1个，则输出某类的样品原始数据的每个变量的均值、最小值、最大值和均方差；

3)如果某类中样品个数为1个，则输出某类的样品原始数据的各变量值；

4)输出原始数据每个变量(j=1，2，…，M)的均值，最小值，最大值和均方差。

(12)结束。

七、无模式识别总体算法流程图

Kohonen无模式总体算法流程图见附图5。

4、深度神经网络具体的工作流程是什么样的？

第一，深度神经网络不是黑盒，个人电脑开机直到神经网络运行在内存中的每一比特的变化都是可以很细微的观察的。没有任何神秘力量，没有超出科学解释的现象发生。第二，深度神经网络的工作方式是基于传统的电脑架构之上的，就是数据+算法。但人们确实从中窥探到了一种全新的电子大脑方式。所以目前有研究提炼一些常用神经网络算法加速硬件。微软等巨头则在开发量子计算。第三，深度神经网络是一个很初级的特征自动提取器。说初级因为简单粗暴。以前为了节约算力特征关键模型都是人工亲自设定。而现在这部分工作随着算力的提高可以自动化。所以从某种意义上来说深度神经网络也是一种自动编程机，但和人们相比，一点点小小的自动化都需要很多很多的计算力支持，这一点也不重要，重要的是，它能工作(手动英文)。那么深度神经网络究竟是什么呢？它是一个能迭代更新自己的特征提取算法。现在这个算法可是像全自动高级工厂，数据往里一丢，不得了！整个工厂里面所有机器都动了起来。没见过的小伙伴当场就被吓呆瓜了，用流行的话说叫懵住。几千只机械手把数据搬来搬去，拿出魔方一样的盒子装来装去又倒出来。整个场面就叫一个震撼。算法运行规模也更大了。

5、神经网络算法原理

4.2.1 概述

人工神经网络的研究与计算机的研究几乎是同步发展的。1943年心理学家McCulloch和数学家Pitts合作提出了形式神经元的数学模型，20世纪50年代末，Rosenblatt提出了感知器模型，1982年，Hopfiled引入了能量函数的概念提出了神经网络的一种数学模型，1986年，Rumelhart及LeCun等学者提出了多层感知器的反向传播算法等。

神经网络技术在众多研究者的努力下，理论上日趋完善，算法种类不断增加。目前，有关神经网络的理论研究成果很多，出版了不少有关基础理论的著作，并且现在仍是全球非线性科学研究的热点之一。

神经网络是一种通过模拟人的大脑神经结构去实现人脑智能活动功能的信息处理系统，它具有人脑的基本功能，但又不是人脑的真实写照。它是人脑的一种抽象、简化和模拟模型，故称之为人工神经网络（边肇祺，2000）。

人工神经元是神经网络的节点，是神经网络的最重要组成部分之一。目前，有关神经元的模型种类繁多，最常用最简单的模型是由阈值函数、Sigmoid 函数构成的模型（图 4-3）。

图4-3 人工神经元与两种常见的输出函数

神经网络学习及识别方法最初是借鉴人脑神经元的学习识别过程提出的。输入参数好比神经元接收信号，通过一定的权值（相当于刺激神经兴奋的强度）与神经元相连，这一过程有些类似于多元线性回归，但模拟的非线性特征是通过下一步骤体现的，即通过设定一阈值（神经元兴奋极限）来确定神经元的兴奋模式，经输出运算得到输出结果。经过大量样本进入网络系统学习训练之后，连接输入信号与神经元之间的权值达到稳定并可最大限度地符合已经经过训练的学习样本。在被确认网络结构的合理性和学习效果的高精度之后，将待预测样本输入参数代入网络，达到参数预测的目的。

4.2.2 反向传播算法（BP法）

发展到目前为止，神经网络模型不下十几种，如前馈神经网络、感知器、Hopfiled 网络、径向基函数网络、反向传播算法（BP法）等，但在储层参数反演方面，目前比较成熟比较流行的网络类型是误差反向传播神经网络（BP-ANN）。

BP网络是在前馈神经网络的基础上发展起来的，始终有一个输入层（它包含的节点对应于每个输入变量）和一个输出层（它包含的节点对应于每个输出值），以及至少有一个具有任意节点数的隐含层（又称中间层）。在 BP-ANN中，相邻层的节点通过一个任意初始权值全部相连，但同一层内各节点间互不相连。对于 BP-ANN，隐含层和输出层节点的基函数必须是连续的、单调递增的，当输入趋于正或负无穷大时，它应该接近于某一固定值，也就是说，基函数为“S”型（Kosko，1992）。BP-ANN 的训练是一个监督学习过程，涉及两个数据集，即训练数据集和监督数据集。

给网络的输入层提供一组输入信息，使其通过网络而在输出层上产生逼近期望输出的过程，称之为网络的学习，或称对网络进行训练，实现这一步骤的方法则称为学习算法。BP网络的学习过程包括两个阶段：第一个阶段是正向过程，将输入变量通过输入层经隐层逐层计算各单元的输出值；第二阶段是反向传播过程，由输出误差逐层向前算出隐层各单元的误差，并用此误差修正前层权值。误差信息通过网络反向传播，遵循误差逐步降低的原则来调整权值，直到达到满意的输出为止。网络经过学习以后，一组合适的、稳定的权值连接权被固定下来，将待预测样本作为输入层参数，网络经过向前传播便可以得到输出结果，这就是网络的预测。

反向传播算法主要步骤如下：首先选定权系数初始值，然后重复下述过程直至收敛（对各样本依次计算）。

（1）从前向后各层计算各单元Oj

储层特征研究与预测

（2）对输出层计算δj

储层特征研究与预测

（3）从后向前计算各隐层δj

储层特征研究与预测

（4）计算并保存各权值修正量

储层特征研究与预测

（5）修正权值

储层特征研究与预测

以上算法是对每个样本作权值修正，也可以对各个样本计算δj后求和，按总误差修正权值。