深度学习（一）多层神经网络，nn.Module搭建和保存网络

多层神经网络（nn.Module）

上节我们讲了神经网络，可以看到使用了激活函数之后，神经网络可以通过改变权重实现任意形状，越是复杂的神经网络能拟合的形状越复杂，可以任意逼近非线性函数，这就是著名的 神经网络万有逼近定理。

下面用实例来说明神经网络效果更好。

import torch
import numpy as np
from torch import nn
import torch.nn.functional as F

import matplotlib.pyplot as plt

%matplotlib inline

定义了画决策边界的函数：

def plot_decision_boundary(model, x, y):
    # Set min and max values and give it some padding
    x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)

创建一个复杂的二分类数据集：

np.random.seed(1)
m = 400 # 样本数量
N = int(m/2) # 每一类的点的个数
D = 2 # 维度
x = np.zeros((m, D))
y = np.zeros((m, 1), dtype='uint8') # label 向量，0 表示红色，1 表示蓝色
a = 4

for j in range(2):
    ix = range(N*j,N*(j+1))
    t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
    r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
    x[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
    y[ix] = j

plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)

1. Logistic回归

x = torch.from_numpy(x).float()
y = torch.from_numpy(y).float()
w = nn.Parameter(torch.randn(2, 1))
b = nn.Parameter(torch.zeros(1))

optimizer = torch.optim.SGD([w, b], 1e-1)

def logistic_regression(x):
    return torch.mm(x, w) + b

criterion = nn.BCEWithLogitsLoss()
for e in range(100):
    out = logistic_regression(x)
    loss = criterion(out,y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if (e + 1) % 20 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.item()))

epoch: 20, loss: 0.8296127319335938
epoch: 40, loss: 0.6758161783218384
epoch: 60, loss: 0.673226535320282
epoch: 80, loss: 0.6731582880020142
epoch: 100, loss: 0.6731503009796143

注意：loss用.item()取出，tensor在计算的时候大多都是float(),torch.Tensor()默认也是float.所以类型不对时，记得转成float。float是32位。double是64位，占内存一般不使用。

x=np.array([1,2])
x1=torch.from_numpy(x).float()
x1.type()
>>>'torch.FloatTensor'

def plot_logistic(x):
    x = torch.from_numpy(x).float()
    out = F.sigmoid(logistic_regression(x))
    out = (out > 0.5) * 1
    return out.data.numpy()

plot_decision_boundary(lambda x: plot_logistic(x), x.numpy(), y.numpy())
plt.title('logistic regression')

plot_decision_boundary画决策边界的函数。使用的时候:

plot_decision_boundary(lambda x: clf.predict(x), X, Y)  # 预测X, Y对应坐标

2.神经网络

# 定义两层神经网络的参数
w1 = nn.Parameter(torch.randn(2, 4) * 0.01) # 隐藏层神经元个数 2
b1 = nn.Parameter(torch.zeros(4))

w2 = nn.Parameter(torch.randn(4, 1) * 0.01)
b2 = nn.Parameter(torch.zeros(1))

# 定义模型
def two_network(x):
    x1 = torch.mm(x, w1) + b1
    x1 = torch.tanh(x1) # 使用 PyTorch 自带的 tanh 激活函数
    x2 = torch.mm(x1, w2) + b2
    return x2

optimizer = torch.optim.SGD([w1, w2, b1, b2], 1.)

criterion = nn.BCEWithLogitsLoss()

# 训练 10000 次
for e in range(10000):
    out = two_network(x)
    loss = criterion(out, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if (e + 1) % 1000 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.item()))

epoch: 1000, loss: 0.24272924661636353
epoch: 2000, loss: 0.24270164966583252
epoch: 3000, loss: 0.24267467856407166
epoch: 4000, loss: 0.24264806509017944
epoch: 5000, loss: 0.24262157082557678
epoch: 6000, loss: 0.24259501695632935
epoch: 7000, loss: 0.24256888031959534
epoch: 8000, loss: 0.24254287779331207
epoch: 9000, loss: 0.24251733720302582
epoch: 10000, loss: 0.24249215424060822

def plot_network(x):
    x = torch.from_numpy(x).float()
    x1 = torch.mm(x, w1) + b1
    x1 = torch.tanh(x1)
    x2 = torch.mm(x1, w2) + b2
    out = torch.sigmoid(x2)
    out = (out > 0.5) * 1
    return out.data.numpy()

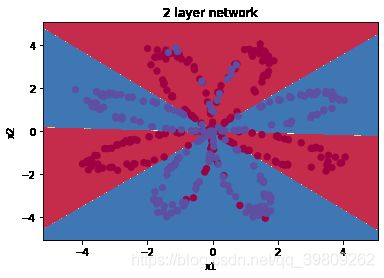
plot_decision_boundary(lambda x: plot_network(x), x.numpy(), y.numpy())
plt.title('2 layer network')

Text(0.5, 1.0, '2 layer network')

可以看到神经网络能够非常好地分类这个复杂的数据，和前面的 logistic 回归相比，神经网络因为有了激活函数的存在，成了一个非线性分类器，所以神经网络分类的边界更加复杂。

3.nn.Module

我们讲了数据处理，模型构建，loss 函数设计等等内容，但是目前为止我们还没有准备好构建一个完整的机器学习系统，一个完整的机器学习系统需要我们不断地读写模型。在现实应用中，一般我们会将模型在本地进行训练，然后保存模型，接着我们会将模型部署到不同的地方进行应用，所以在这节将会讲解如何保存 PyTorch 的模型。

对于前面的线性回归模型、 Logistic回归模型和神经网络，我们在构建的时候定义了需要的参数。这对于比较小的模型是可行的，但是对于大的模型，比如100 层的神经网络，这个时候再去手动定义参数就显得非常麻烦，所以 PyTorch 提供了两个模块来帮助我们构建模型，一个是Sequential，一个是Module。

Sequential允许我们构建序列化的模块，他不包含线性层。而 Module 是一种更加灵活的模型定义方式，推荐使用，下面Module 来定义上面的神经网络。

Module模板：

lass 网络名字(nn.Module):
    def __init__(self, 一些定义的参数):
        super(网络名字, self).__init__()
        self.layer1 = nn.Linear(num_input, num_hidden)
        self.layer2 = nn.Sequential(...)
        ...

        定义需要用的网络层

    def forward(self, x): # 定义前向传播
        x1 = self.layer1(x)
        x2 = self.layer2(x)
        x = x1 + x2
        ...
        return x

# 我们训练 10000 次
for e in range(10000):
    out = seq_net(Variable(x))
    loss = criterion(out, Variable(y))
    optim.zero_grad()
    loss.backward()
    optim.step()
    if (e + 1) % 1000 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.data[0]))

注意的是，Module 里面也可以使用 Sequential，同时 Module 非常灵活，具体体现在 forward 中，如何复杂的操作都能直观的在 forward 里面执行:

class module_net(nn.Module):
    def __init__(self, num_input, num_hidden, num_output):
        super(module_net, self).__init__()
        self.layer1 = nn.Linear(num_input, num_hidden)

        self.layer2 = nn.Tanh()

        self.layer3 = nn.Linear(num_hidden, num_output)

    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x

mo_net = module_net(2, 4, 1) #实例化

# 访问模型中的某层可以直接通过名字
# 第一层
l1 = mo_net.layer1
print(l1)

# 打印出第一层的权重
print(l1.weight)

# 定义优化器
optim = torch.optim.SGD(mo_net.parameters(), 1.)

# 我们训练 10000 次
for e in range(10000):
    out = mo_net(x)
    loss = criterion(out,y)
    optim.zero_grad()
    loss.backward()
    optim.step()
    if (e + 1) % 1000 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.item()))

Linear(in_features=2, out_features=4, bias=True)
Parameter containing:
tensor([[ 0.1956, -0.6409],
        [ 0.0387, -0.1851],
        [ 0.6011, -0.2028],
        [ 0.0779,  0.2532]], requires_grad=True)
epoch: 1000, loss: 0.2929742932319641
epoch: 2000, loss: 0.2804087698459625
epoch: 3000, loss: 0.27174893021583557
epoch: 4000, loss: 0.2664014995098114
epoch: 5000, loss: 0.2626623213291168
epoch: 6000, loss: 0.25987517833709717
epoch: 7000, loss: 0.2577124238014221
epoch: 8000, loss: 0.25597918033599854
epoch: 9000, loss: 0.25455164909362793
epoch: 10000, loss: 0.2533482611179352

保存模型:

torch.save(mo_net.state_dict(), 'module_net.pth')

验证state_dict():

def main():

    # print model's state_dict
    print('Model.state_dict:')
    for param_tensor in mo_net.state_dict():
        #打印 key value字典
        print(param_tensor,'\t',mo_net.state_dict()[param_tensor].size())
 
    # print optimizer's state_dict
    print('Optimizer,s state_dict:')
    for var_name in optimizer.state_dict():
        print(var_name,'\t',optimizer.state_dict()[var_name])# 注意这里用optim和optimizer一样的效果

if __name__=='__main__':
    main()

Model.state_dict:
layer1.weight 	 torch.Size([4, 2])
layer1.bias 	 torch.Size([4])
layer3.weight 	 torch.Size([1, 4])
layer3.bias 	 torch.Size([1])
Optimizer,s state_dict:
state 	 {}
param_groups 	 [{'lr': 1.0, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0, 1, 2, 3]}]

在pytorch中，torch.nn.Module模块中的state_dict变量存放训练过程中需要学习的权重和偏置系数，state_dict作为python的字典对象将每一层的参数映射成tensor张量，需要注意的是torch.nn.Module模块中的state_dict只包含卷积层和全连接层的参数。

torch.optim模块中的Optimizer优化器对象也存在一个state_dict对象，此处的state_dict字典对象包含state和param_groups的字典对象，而param_groups key对应的value也是一个由学习率，动量等参数组成的一个字典对象。

因为state_dict本质上Python字典对象，所以可以很好地进行保存、更新、修改和恢复操作（python字典结构的特性），从而为PyTorch模型和优化器增加了大量的模块化。

参考：深度学习入门之PyTorch