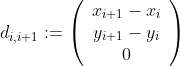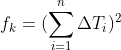深度科普：拆解让机器人走路更「丝滑」的TEB算法

导航模块，是实现机器人移动功能的重要能力，主要包括全局路径规划和局部路径规划。本文将带大家深度认识局部路径规划，以及TEB算法的规划原理和参数配置。

01 机器人局部路径规划

当我们旅游迷路了，想必大家都会毫不犹豫地——

打开手机，点开地图APP，开始「导航」。

 其实，不止我们人类，机器人也会用到「导航」功能，只不过这个功能是它们自带的。

无论是在某底捞的送餐机器人，还是某朵酒店的配送机器人，又或者是智能工厂里的真·机器人搬运工……

​都是机器人通过自己的导航模块，为自己规划出一条移动路径，然后控制底盘安全稳定地完成移动。

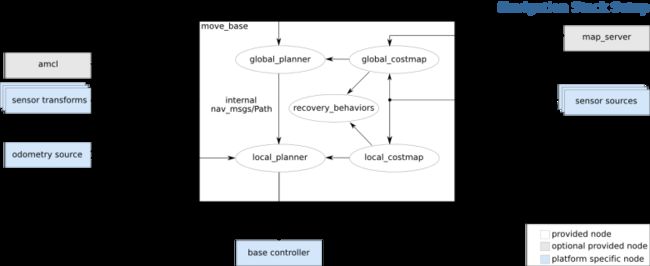
我们以机器人操作系统ROS为例，导航模块输出了Twist类型的速度指令后，将其下发到底盘，就成为了底盘运动的直接依据。

其中，最终向机器人底盘下发速度指令的部分，就是「局部路径规划」。

​由于这个速度指令，不仅要遵循全局路径规划给出的路径，还需实时避开路径上的障碍物，导致算法需要频繁调用、高速响应，通常要将全局路径进行分割。

也就是说，只考虑当前点附近的路径和障碍物进行规划。「局部路径规划」因此而得名。

02 TEB算法规划原理

DWA、TEB、Trajectory Rollout是三种常用的局部路径规划算法。其中，TEB算法有很强的前瞻性，能够动态避障，表现较好，缺点是计算复杂——这也是其使用g2o算法优化计算量的原因。

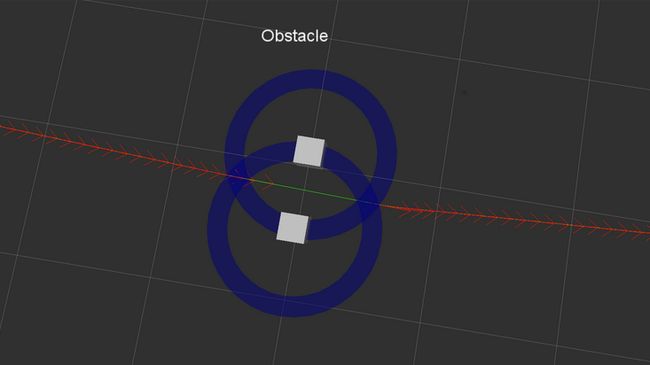
TEB全称是Timed Elastic Band，译为时间橡皮筋。好比导航的起点和终点之间，拉了一条绷直的橡皮筋作为行走路线，如果路中间有障碍物，就会将橡皮筋撑开，影响行走时的路径。

就像这样：

 当然，在实际情况中，机器人的行走路线会受到许多其他因素的影响，不会紧贴着障碍物表面。我们通常会将障碍物进行膨胀处理，让机器人的行走路线与真实的障碍物之间，保持一定的安全距离。

 在TEB算法中，所有影响因素分为两类：约束和轨迹。

约束指的是速度和加速度的限制，这些往往由机器人本身决定；轨迹则指最短或最快的路径，或者与障碍物保持距离，又或者是与规划路径尽可能地跟随。

一般来说，TEB算法会通过参数的方式，调整各影响因素的权重，为每个影响因素设计奖励或者惩罚函数，然后对可行的路线进行打分，最后选择得分最高的局部路线下发速度指令。

这样规划出的路径，更符合小车的硬件结构以及运动学，能够让小车流畅地行驶和绕障，且行驶速度和到点时间都有着优秀表现。

但由于需考虑的参数较多，如何「合理地」配置参数，就成了最重要且最困难的一环。

03 如何为TEB算法配置参数？

典型的「障碍物和中间点参数配置」

通常来说，我们会希望为机器人规划出一条远离障碍物，又尽可能经过中间点的路线，让机器人的行走路线更合理。基于此，我们可以在TEB算法中，对障碍物和中间点分别配置参数，并运用到惩罚函数中。

TEB与障碍物的最小距离演示，Xn为TEB路径点，Zj为障碍物

一方面，为远离障碍物，我们需要为机器人设置障碍物距离、障碍物膨胀距离，以及障碍物的权重等障碍物参数，对靠近障碍物的路线进行惩罚。

另一方面，为尽可能经过路线中间点，我们可以以相反的目的进行参数设置，如中间点权重、中间点间隔和中间点顺序等，对远离中间点的路线进行惩罚。

具体的惩罚公式如下：

（惩罚函数， 为TEB路径距离障碍物的实际最小距离， 为参数定义的最小距离）

由于障碍物和中间点相互独立，有时会出现障碍物阻挡在TEB路径，或中间点坐落在障碍物内部的情况。

这两种参数就像橡皮筋上的同一个点，受到相反方向两个力的牵制，一旦权衡控制不当，就会让机器人陷入局部最优困境，增大绕障时间，甚至让机器人撞向障碍物。

局部最优困境演示

​

更复杂的「速度和加速度参数配置」

TEB算法还考虑到了机器人本身速度和加速度的限制，如对线速度、角速度、线加速度、角加速度各自的最大限制和到达最大值的权重进行参数配置。

首先，速度约束在TEB中能用固定时间间隔的特性解释。TEB路线中某一点的速度，可以由其前后点的距离推出：

（  为TEB规定的两点间时间间隔）

同理，在得到速度之后，可以用同样的时间间隔推出加速度：

在差分驱动机器人上，车轮的速度可以表示为：

（  为机器人轴距的一半）

之后再进一步微分，就能得到车轮的加速度。最后，根据计算出的车轮速度与由最大速度制定的损失函数综合考虑，就能制定出固定时间下速度和位移合适的路线。

比某芙还丝滑的「运动学约束」

有些机器人底盘还会受到运动学约束，如差分驱动机器人，它在平面运动中只有两个自由度，只能在机器人朝向上执行运动。因此还需要进行运动学约束，规划出一条相对平滑的路线，让机器人走得更丝滑。

TEB路径规划就考虑到了这点，同样以差分驱动机器人为例：

（  表示  点上机器人的绝对角度）

得出的方向向量为：

相应的目标函数为：

最后也是最根本的「最快路径轨迹约束」

最快路径轨迹约束，其实就是时间约束，需要对最优时间权重进行参数设置。即间接地对TEB路径点之间的时间间隔进行控制，从而影响最终到达时间。

如果TEB路径点之间的时间间隔是一致的，那么最终规划出的轨迹，就是约束后时间最短的路径轨迹。具体可以通过最小化所有时间间隔之和的平方来实现，这也是TEB算法最根本的特征和优势。

总的来说，我们在实践过程中，要根据TEB算法的规划原理，依次考虑障碍物和中间点、速度和加速度、运动学约束以及最快路径轨迹约束等参数配置，才能让机器人走出流畅又丝滑的步伐。

至于约束和轨迹，如何通过g2o——图优化算法来具体实施？我们之后再为大家拆解。

参考资料：

[1] Roesmann C ,  Feiten W ,  Woesch T , et al. Trajectory modification considering dynamic constraints of autonomous robots[C]// Robotics Proceedings of ROBOTIK 2012 7th German Conference on. VDE, 2012.

[2] http://wiki.ros.org/cn/navigation

[3] https://www.cnblogs.com/gary-guo/p/10894325.html