吴恩达机器学习ex6任务1代码

import pandas as pd
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt
from sklearn.svm import SVC


'''===================================函数部分=================================='''
'''数据分类'''
def classify(X,y):
    pos_data = []
    neg_data = []
    for i in range(X.shape[0]):
        if y[i, 0] == 1:
            pos_data.append(X[i, :])
        elif y[i, 0] == 0:
            neg_data.append(X[i, :])
    pos_data = np.array(pos_data)
    neg_data = np.array(neg_data)
    return pos_data, neg_data



'''线性支持向量机'''
def svc_func(X,y,c):
    svc = SVC(C=c,kernel='linear')   #C为惩罚系数，核函数选择线性核
    model = svc.fit(X,y.flatten())   #导入数据
    return model


'''===================================计算部分=================================='''
'''数据可视化其一'''
# plt.figure(figsize=(12,8))
data1 = loadmat('D:\新大陆\吴恩达机器学习\ex6\ex6data1.mat')
X_raw = data1['X']   #51,2
y_raw = data1['y']   #51,1
pos_data1, neg_data1 = classify(X_raw,y_raw)
plt.scatter(pos_data1[:,0], pos_data1[:,1], c='g', marker='+')
plt.scatter(neg_data1[:,0], neg_data1[:,1], c='r', marker='o')
plt.xlim(0,4.5)
plt.ylim(1.5,5)
# plt.show()



'''运行支持向量机'''
C = 1
svc1 = svc_func(X_raw,y_raw,C)
score = svc1.score(X_raw,y_raw.flatten())   #准确率
print(score)



'''支持向量机可视化图像'''
# plt.figure(figsize=(12,8))
xx = np.linspace(start=X_raw[:,0].min(), stop=X_raw[:,0].max(), num=1000)   #1000,
yy = np.linspace(start=X_raw[:,1].min(), stop=X_raw[:,1].max(), num=1000)   #1000,
XX, YY = np.meshgrid(xx, yy)   #XX: array(1000,1000),把给的数组当成行，重复第一行；  YY:array(1000,1000)，把给的数组当成列，重复第一列
# print('XX',XX)
# print('YY',YY)
p = svc1.predict(np.concatenate((XX.reshape(-1, 1), YY.reshape(-1, 1)), axis=1))   #reshape按行拆开。concatenate将数组拼接起来，axis=1是（1000000，1+1），axis=0时（1000000+1000000，1）
plt.scatter(pos_data1[:,0], pos_data1[:,1], c='g', marker='+')
plt.scatter(neg_data1[:,0], neg_data1[:,1], c='r', marker='o')
plt.contour(xx, yy, p.reshape(XX.shape))   #1000,   1000,   1000,
plt.xlim(0,4.5)
plt.ylim(1.5,5)
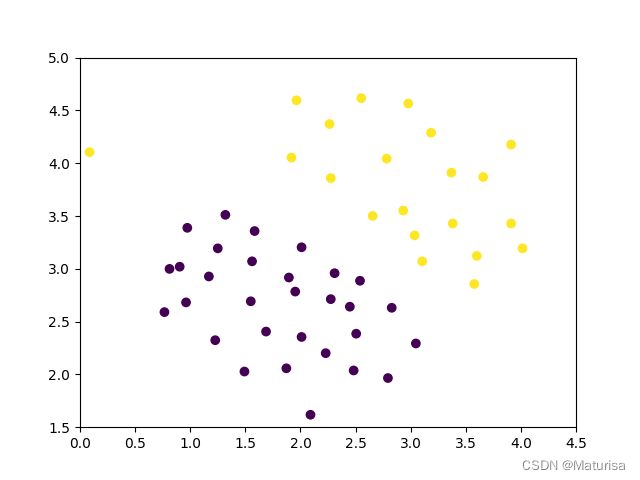
# plt.show()

ex6data1原始数据图像化：

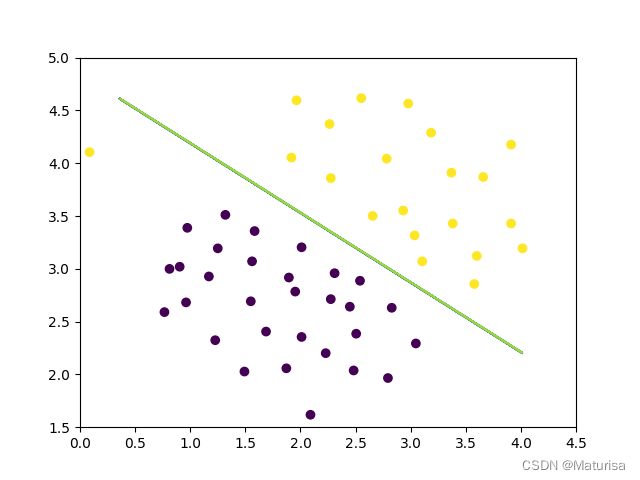
决策边界（C=1）：

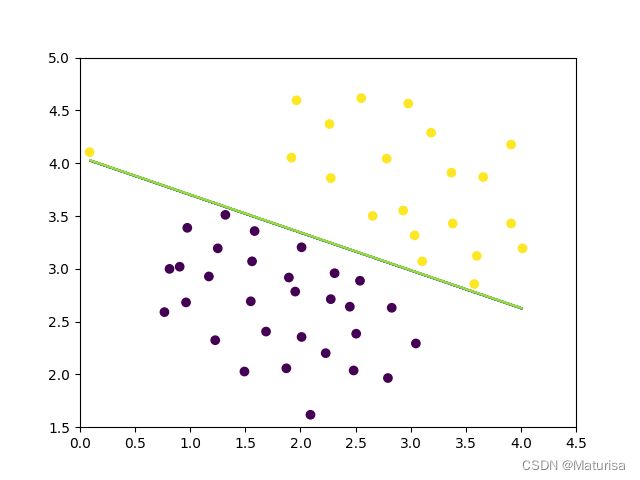
 决策边界（C=100）：

'''数据可视化其二'''
# plt.figure(figsize=(12,8))
data2 = loadmat('D:\新大陆\吴恩达机器学习\ex6\ex6data2.mat')
X_raw2 = data2['X']   #863,2
y_raw2 = data2['y']
pos_data2, neg_data2 = classify(X_raw2,y_raw2)
plt.scatter(pos_data2[:,0], pos_data2[:,1], c='g', marker='+')
plt.scatter(neg_data2[:,0], neg_data2[:,1], c='r', marker='o')
# plt.show()



'''画高斯图像'''
# gamma = 1 / (2 * np.power(sigma, 2))
#高斯核函数中的gamma越大，相当高斯函数中的σ越小，越可能过拟合
#高斯核函数中的gamma越小，相当高斯函数中的σ越大，越可能欠拟合
svc2 = SVC(C=1, kernel='rbf', gamma=50)
svc2.fit(X_raw2, y_raw2.flatten())

# plt.figure(figsize=(12,8))
xx = np.linspace(start=X_raw2[:,0].min(), stop=X_raw2[:,0].max(), num=1000)
yy = np.linspace(start=X_raw2[:,1].min(), stop=X_raw2[:,1].max(), num=1000)
XX, YY = np.meshgrid(xx, yy)

p = svc2.predict(np.concatenate((XX.reshape(-1, 1), YY.reshape(-1, 1)), axis=1))   #reshape按行拆开。concatenate将数组拼接起来
plt.scatter(pos_data2[:,0], pos_data2[:,1], c='g', marker='+')
plt.scatter(neg_data2[:,0], neg_data2[:,1], c='r', marker='o')
plt.contour(xx, yy, p.reshape(XX.shape))
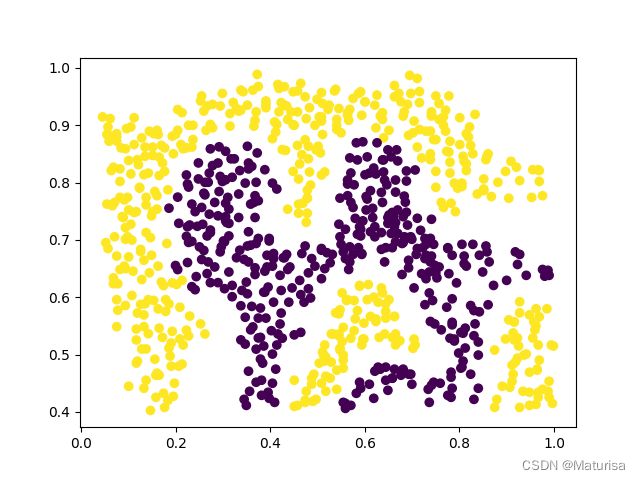
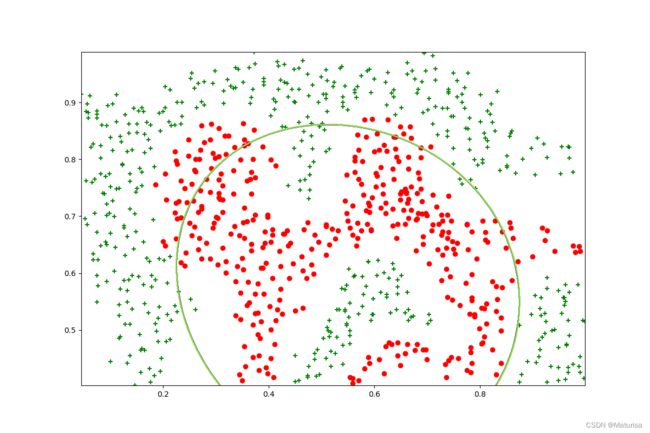
# plt.show()

ex6data2数据图像化：

决策边界（C=1，gamma=1，注意是gamma不是σ）：

欠拟合

 

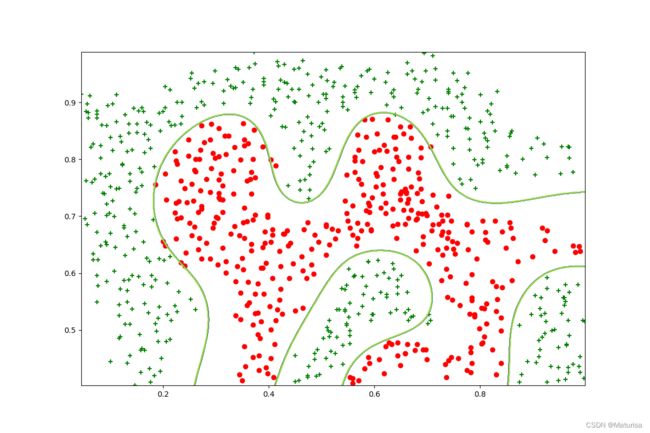
决策边界（C=1，gamma=50）：

恰好

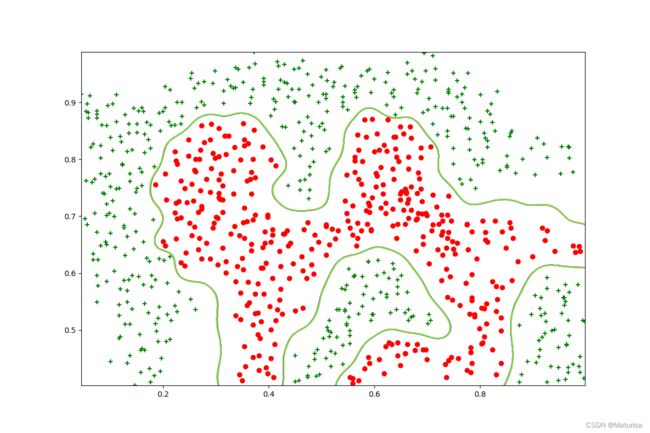
决策边界（C=1，gamma=100）：

过拟合

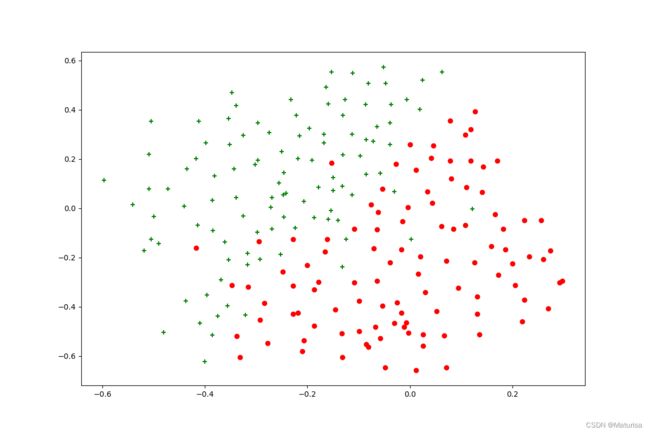
'''数据可视化其三'''
data3 = loadmat('D:\新大陆\吴恩达机器学习\ex6\ex6data3.mat')
X_raw3 = data3['X']
y_raw3 = data3['y']
Xval = data3['Xval']   #200,2
yval = data3['yval']

# plt.figure(figsize=(12,8))
pos_data3, neg_data3 = classify(X_raw3,y_raw3)
plt.scatter(pos_data3[:,0], pos_data3[:,1], c='g', marker='+')
plt.scatter(neg_data3[:,0], neg_data3[:,1], c='r', marker='o')
# plt.show()



'''找C和σ，并画出训练好的曲线'''
xx, yy = np.meshgrid(np.array([0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]), np.array([0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]))
# print('xx',xx)
# print('yy',yy)
parameters = np.concatenate((xx.reshape(-1, 1), yy.reshape(-1, 1)), axis=1)   #64,2。相当于展示了8个数和8个数组合的64种可能性
# print(parameters)
score = []
for C, sigma in parameters:   #这种写法是，一次取一行
    # print(C,sigma)
    gamma = 1 / (2 * np.power(sigma, 2))
    model = SVC(C=C, kernel='rbf', gamma=gamma)
    model.fit(X_raw3, y_raw3.flatten())   #用train训练
    score = np.append(score, model.score(Xval, yval.flatten()))   #用val检测. 64,
res = np.concatenate((parameters, score.reshape(-1, 1)), axis=1)   #64,3
index = np.argmax(res, axis=0)[2]   #在res各行（axis=0）第3列（【2】，这里写-1也行，代表最后一列）中取最大值，返回其行编号
print("参数的最好选择是 :C=", res[index,0], ",sigma=", res[index,1], ",得分=", res[index,2])
# the best choice of parameters:C= 1.0 ,sigma= 0.1 ,score= 0.965
plt.show()



'''当c=1，sigma=1时的边界线'''
sigma = 0.1
svc3 = SVC(C=1, kernel='rbf', gamma=1 / (2 * np.power(sigma, 2)))
svc3.fit(X_raw3, y_raw3.flatten())

plt.figure(figsize=(12,8))
xx = np.linspace(start=X_raw3[:,0].min(), stop=X_raw3[:,0].max(), num=1000)
yy = np.linspace(start=X_raw3[:,1].min(), stop=X_raw3[:,1].max(), num=1000)
XX, YY = np.meshgrid(xx, yy)
p = svc3.predict(np.concatenate((XX.reshape(-1, 1), YY.reshape(-1, 1)), axis=1))   #reshape按行拆开。concatenate将数组拼接起来
plt.scatter(pos_data3[:,0], pos_data3[:,1], c='g', marker='+')
plt.scatter(neg_data3[:,0], neg_data3[:,1], c='r', marker='o')
plt.contour(xx, yy, p.reshape(XX.shape))
plt.show()

ex6data3数据图像化：

在8个σ，8个C中选择最优参数，筛选代码参考大佬  說詤榢  的代码  6. 吴恩达机器学习课程-作业6-SVM，感谢。

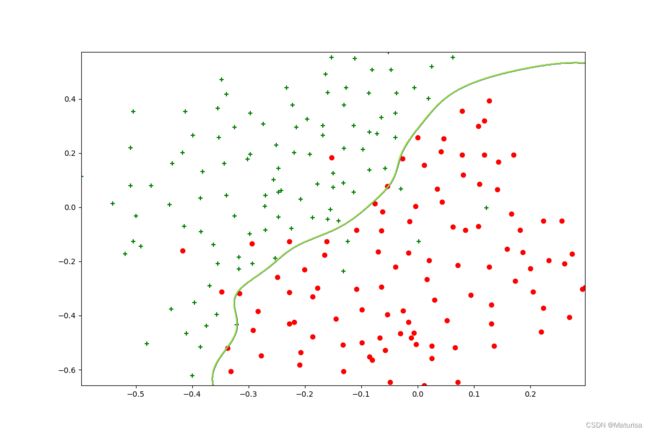
筛选出C=1，σ=0.1为最优解，用val数据集验证准确度0.965。此时的决策边界为：

任务一结束。

感谢所有在机器学习道路上的引路人。