机器学习（二）之无监督学习：数据变换、聚类分析

0 本文简介

本文根据Andreas C.Muller的《Introduction to Machine Learning with Python》，不涉及复杂的数学理论，整理了常见的无监督学习模型的思想、应用、优缺点等问题。

相关笔记：
机器学习（一）之 2万多字的监督学习模型总结V1.0：K近邻、线性回归、岭回归、朴素贝叶斯模型、决策树、随机森林、梯度提升回归树、SVM、神经网络
机器学习（二）之无监督学习：数据变换、聚类分析
机器学习（三）之数据表示和特征工程：One-Hot编码、分箱处理、交互特征、多项式特征、单变量非线性变换、自动化特征选择
机器学习（四）之参数选择：交叉验证、网格搜索
机器学习（五）之评价指标：二分类指标、多分类指标、混淆矩阵、不确定性、ROC曲线、AUC、回归指标

1 无监督学习概述

无监督学习算法只有输入数据，而没有已知的输出标签（label)，我们需要从这些数据中学习到信息。常见的无监督学习包括数据集变换和聚类。

数据集的**无监督变换（unsupervised transformation）**是创建数据新的表示的算法，与数据的原始表示相比，新的表示可能更容易被人或其他机器学习算法所理解。无监督变换的一个常见应用是降维（dimensionality reduction），降维的一个常见应用是为了可视化将数据降为二维。无监督变换的另一个应用是找到“构成”数据的各个组成部分。

聚类算法（clustering algorithm) 将数据划分成不同的组，每组包含相似的内容。

无监督学习的一个主要挑战就是评估算法是否学到了有用的东西。我们不知道正确的输出应该是什么，很难判断一个模型是否“表现很好”。，通常来说，评估无监督算法结果的唯一方法就是人工检查。

因此，如果数据科学家想要更好地理解数据，那么无监督算法通常可用于探索性的目的，而不是作为大型自动化系统的一部分。无监督算法的另一个常见应用是作为监督算法的预处理步骤。学习数据的一种新表示，有时可以提高监督算法的精度，或者可以减少内存占用和时间开销。

2 数据集变换

2.1 预处理和缩放

在监督学习中，诸如神经网络、SVM，对数据缩放非常敏感。因此，通常的做法是对特征进行调节，使数据表示更适合于这些算法。通常来说，这是对数据的一种简单的按特征的缩放和移动。

scikit-learn中常见的缩放命令有：

1. StandardScaler : 确保每个特征的平均值为0、方差为1，使所有特征都位于同一量级。但不能保证特征任何特定的最大值和最小值。
2. RobustScaler：使用中位数和四分位，而不是平均值和方差，确保每个特征的统计属性都位于同一范围。但是会忽略异常值（outlier）
3. MinMaxScaler：移动数据，使所有特征都刚好位于0 到1 之间。对于二维数据集来说，所有的数据都包含在x 轴0 到1 与y 轴0 到1 组成的矩形中。
4. Normalizer：对每个数据点进行缩放，使得特征向量的欧式长度等于1。即它将一个数据点投射到半径为1 的圆上（对于更高维度的情况，是球面）。这意味着每个数据点的缩放比例都不相同（乘以其长度的倒数）。如果只有数据的方向（或角度）是重要的，而特征向量的长度无关紧要，那么通常会使用这种归一化。

中位数指的是这样的数值x：有一半数值小于x，另一半数值大于x。较小四分位数指的是这样的数值x：有四分之一的数值小于x。较大四分位数指的是这样的数值x：有四分之一的数值大于x。

2.2 程序实现

使用scikit-learn实现如下：

# 我们首先导入实现预处理的类，然后将其实例化
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
# 使用fit 方法拟合缩放器（scaler），并将其应用于训练数据
scaler.fit(X_train)
# 变换数据，对数据进行实际缩放
X_train_scaled = scaler.transform(X_train)
# 通过对X_test调用transform方法来完成对测试集的变换
# 对测试数据进行变换
X_test_scaled = scaler.transform(X_test)

这里需要注意，MinMaxScaler（以及其他所有缩放器）总是对训练集和测试集应用完全相同的变换。也就是说，transform 方法总是减去训练集的最小值，然后除以训练集的范围，而这两个值可能与测试集的最小值和范围并不相同。因此，不能将训练集和测试集分开缩放

快捷方式与高效的替代方法：

通常来说，想要在某个数据集上fit 一个模型，然后再将其transform。通常可以用比先调用fit 再调用transform 更高效的方法来计算。对于这种使用场景，所有具有transform 方法的模型也都具有一个fit_transform 方法>。下面是使用StandardScaler 的一个例子：

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# 依次调用fit和transform（使用方法链）
X_scaled = scaler.fit(X).transform(X)
# 结果相同，但计算更加高效
X_scaled_d = scaler.fit_transform(X)

虽fit_transform不一定对所有模型都更加高效，但在尝试变换训练集时，使用这一方法仍然是很好的做法。

2.3 降维、特征提取与流形学习

数据变换最常见的目的就是可视化、压缩数据，以及寻找信息量更大的数据表示以用于进一步的处理。常见的算法有主成分分析、非负矩阵分解、t-SNE，前者通常用于特征提取，后者通常用于二维散点图的可视化。此外还有独立成分分析（ICA）、因子分析（FA）和稀疏编码（字典学习），可参见链接：http://scikit-learn.org/stable/modules/decomposition.html

2.3.1 主成分分析

主成分分析（principal component analysis，PCA）是一种旋转数据集的方法，旋转后的特征在统计上不相关。在做完这种旋转之后，通常是根据新特征对解释数据的重要性来选择它的一个子集。

算法思路：

step1：找到方差最大的方向，将其标记为“成分1”（Component 1）。这是数据中包含最多信息的方向（或向量）。即，沿着这个方向的特征之间最为相关。

step2：找到与第一个方向正交（成直角）且包含最多信息的方向。

step3：依次找到所有方向，判断是否符合要求。

step4：选择在后续过程中要使用的主成分个数。

利用这一过程找到的方向被称为主成分（principal component），因为它们是数据方差的主要方向。一般来说，主成分的个数与原始特征相同。

应用：

1）、将高维数据集可视化

利用PCA，我们可以获取到主要的相互作用，并得到稍为完整的可视化。PCA 的一个缺点在于，通常不容易对图中的两个轴做出解释。主成分对应于原始数据中的方向，所以它们是原始特征的组合。但这些组合往往非常复杂。

2）、特征提取

特征提取背后的思想是，可以找到一种数据表示，比给定的原始表示更适合于分析。特征提取很有用，它的一个很好的应用实例就是图像。图像由像素组成，通常存储为红绿蓝（RGB）强度。图像中的对象通常由上千个像素组成，它们只有放在一起才有意义。

2.3.2 非负矩阵分解

非负矩阵分解（non-negative matrix factorization，NMF）目的在于提取有用的特征。它的工作原理类似于PCA，将每个数据点写成一些分量的加权求和，也可以用于降维。所不同的是，PCA中我们想要的是正交分量，并且能够解释尽可能多的数据方差。而NMF中，我们希望分量和系数均为非负。因此，这种方法只能应用于每个特征都是非负的数据，因为非负分量的非负求和不可能变为负值。

将数据分解成非负加权求和的这个过程，对由多个独立源相加（或叠加）创建而成的数据特别有用，最适合于具有叠加结构的数据，包括音频、基因表达和文本数据。在这种情况下，NMF 可以识别出组成合成数据的原始分量。总的来说，与PCA 相比，NMF 得到的分量更容易解释，因为负的分量和系数可能会导致难以解释的抵消效应（cancellation effect）。

如果我们仅使用一个分量，那么NMF 会创建一个指向平均值的分量，因为指向这里可以对数据做出最好的解释。你可以看到，与PCA 不同，减少分量个数不仅会删除一些方向，而且会创建一组完全不同的分量！ NMF 的分量也没有按任何特定方法排序，所以不存在“第一非负分量”：所有分量的地位平等。NMF 使用了随机初始化，根据随机种子的不同可能会产生不同的结果。在人脸识别中，PCA找到的是重建的最佳方向。NMF通常并不用于对数据进行重建或编码，而是用于在数据中寻找有趣的模式。

2.3.3 用t-SNE进行流形学习

流形学习算法（manifold learning algorithm），它允许进行更复杂的映射，通常也可以给出更好的可视化。其中特别有用的一个就是t-SNE 算法。

流形学习算法主要用于可视化，因此很少用来生成两个以上的新特征。其中一些算法（包括t-SNE）计算训练数据的一种新表示，但不允许变换新数据。更确切地说，它们只能变换用于训练的数据。流形学习对探索性数据分析是很有用的，但如果最终目标是监督学习的话，则很少使用。

思想：

找到数据的一个二维表示，尽可能地保持数据点之间的距离。t-SNE 首先给出每个数据点的随机二维表示，然后尝试让在原始特征空间中距离较近的点更加靠近，原始特征空间中相距较远的点更加远离。t-SNE 重点关注距离较近的点，而不是保持距离较远的点之间的距离。换句话说，它试图保存能够表示哪些点比较靠近的信息。

这种方法并不知道类别标签：它完全是无监督。但它能够找到数据的一种二维表示，仅根据原始空间中数据点之间的靠近程度就能够将各个类别明确分开。t-SNE 算法有一些调节参数， 默认参数的效果通常就很好。也可以尝试修改perplexity和early_exaggeration，但作用一般很小。

3 聚类

聚类（clustering）是将数据集划分成组的任务，这些组叫作簇（cluster）。其目标是划分数据，使得一个簇内的数据点非常相似且不同簇内的数据点非常不同。本文主要总结K均值聚类、凝聚聚类、DBSCAN。

3.1 K均值聚类

k 均值聚类是最简单也最常用的聚类算法之一。它试图找到代表数据特定区域的簇中心（cluster center）。

算法交替执行以下两个步骤：（1）将每个数据点分配给最近的簇中心；（2）将每个簇中心设置为所分配的所有数据点的平均值。如果簇的分配不再发生变化，那么算法结束。

不适用的情况：

1）、即使知道给定数据集中簇的“正确”个数，k 均值可能也不是总能找到它们。每个簇仅由其中心定义，这意味着每个簇都是凸形（convex）。因此，k 均值只能找到相对简单的形状。k 均值还假设所有簇在某种程度上具有相同的“直径”，它总是将簇之间的边界刚好画在簇中心的中间位置。

2）、k均值还假设所有方向对每个簇都同等重要。如下图所示，一个二维数据集中包含明确分开的三部分。但是这三部分被沿着对角线方向拉长。由于k 均值仅考虑到最近簇中心的距离，所以它无法处理这种类型的数据：

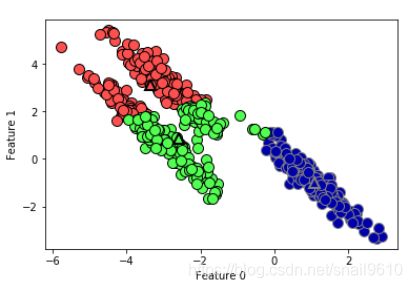
3）、如果簇的形状更加复杂，如下图所示，那k均值的表现也很差

矢量量化，或者将k均值看作分解：

PCA 试图找到数据中方差最大的方向，而NMF 试图找到累加的分量，这通常对应于数据的“极值”或“部分”。两种方法都试图将数据点表示为一些分量之和。与之相反，k 均值则尝试利用簇中心来表示每个数据点。**可以将其看作仅用一个分量来表示每个数据点，该分量由簇中心给出。**这种观点将k 均值看作是一种分解方法，其中每个点用单一分量来表示，这种观点被称为矢量量化（vector quantization）。

再看上图的two_moons 数据，我们利PCA、NMF对这个数据无能为力，因为它只有两个维度，使用PCA 、NMF 将其降到一维，将会完全破坏数据的结构。但通过使用更多的簇中心，可以用k 均值找到一种更具表现力的表示。

如果使用了10 簇中心，即每个点都被分配了0 到9 之间的一个数字。我们可以将其看作10 个分量表示的数据，只有表示该点对应的簇中心的那个特征不为0，其他特征均为0。利用这个10 维表示，现在可以用线性模型来划分两个半月形，而利用原始的两个特征是不可能做到这一点的。将到每个簇中心的距离作为特征，还可以得到一种表现力更强的数据表示，结果如下图所示。可以利用kmeans 的transform 方法来完成这一点：distance_features = kmeans.transform(X)

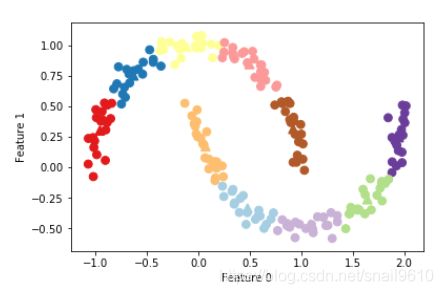
优缺点：

k均值是非常流行的聚类算法，因为它不仅相对容易理解和实现，而且运行速度也相对较快。k均值可以轻松扩展到大型数据集。

k 均值的缺点之一在于，它依赖于随机初始化，也就是说，算法的输出依赖于随机种子。默认情况下，scikit-learn 用10 种不同的随机初始化将算法运行10 次，并返回最佳结果（簇的方差之和最小）。

k 均值另一个缺点是对簇形状的假设的约束性较强，而且还要求指定所要寻找的簇的个数（在现实世界的应用中可能并不知道这个数字）。

3.2 凝聚聚类

凝聚聚类（agglomerative clustering）算法首先声明每个点是自己的簇，然后合并两个最相似的簇，直到满足某种停止准则为止。scikit-learn 中实现的停止准则是簇的个数。还有一些链接（linkage）准则，规定如何度量“最相似的簇”。这种度量总是定义在两个现有的簇之间。值得注意的是，凝聚聚类仍然无法分离像two_moons 数据集这样复杂的形状

scikit-learn 中实现了以下三种选项：

​ ward：默认选项。ward 挑选两个簇来合并，使得所有簇中的方差增加最小。这通常会得到大
小差不多相等的簇。

​ average链接： 将簇中所有点之间平均距离最小的两个簇合并。

​ complete 链接：也称为最大链接，将簇中点之间最大距离最小的两个簇合并。

ward 适用于大多数数据集，在我们的例子中将使用它。如果簇中的成员个数非常不同（比如其中一个比其他所有都大得多），那么average 或complete 可能效果更好。

注意：凝聚算法不能对新数据点做出预测。因此sklearn.cluster中的AgglomerativeClustering没有predict方法。为了构造模型并得到训练集上簇的成员关系，可以改用fit_predict方法,也可以使用labels_属性，正如k 均值所做的那样。

例子：

from sklearn.cluster import AgglomerativeClustering
X, y = make_blobs(random_state=1)
# 需要指定算法找到的簇的个数
agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(X)

mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment)
plt.legend(["Cluster 0", "Cluster 1", "Cluster 2"], loc="best")
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

结果：

虽然凝聚聚类的scikit-learn 实现需要指定希望算法找到的簇的个数，但凝聚聚类方法为选择正确的个数提供了一些帮助。

层次聚类：

凝聚聚类生成了所谓的层次聚类（hierarchical clustering）。聚类过程迭代进行，每个点都从一个单点簇变为属于最终的某个簇。每个中间步骤都提供了数据的一种聚类（簇的个数也不相同）。但它依赖于数据的二维性质，因此不能用于具有两个以上特征的数据集。

例如：mglearn.plots.plot_agglomerative()

树状图：

它可以处理多维数据集。可以使用SciPy生成树状图。SciPy 的聚类算法接口与scikit-learn 的聚类算法稍有不同。SciPy 提供了一个函数，接受数据数组X 并计算出一个链接数组（linkage array），它对层次聚类的相似度进行编码。然后我们可以将这个链接数组提供给scipy的dendrogram函数来绘制树状图。

例如：

# 从SciPy中导入dendrogram函数和ward聚类函数
from scipy.cluster.hierarchy import dendrogram, ward

X, y = make_blobs(random_state=0, n_samples=12)
# 将ward聚类应用于数据数组X
# SciPy的ward函数返回一个数组，指定执行凝聚聚类时跨越的距离
linkage_array = ward(X)
# 现在为包含簇之间距离的linkage_array绘制树状图
dendrogram(linkage_array)

# 在树中标记划分成两个簇或三个簇的位置
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [7.25, 7.25], '--', c='k')
ax.plot(bounds, [4, 4], '--', c='k')

ax.text(bounds[1], 7.25, ' two clusters', va='center', fontdict={'size': 15})
ax.text(bounds[1], 4, ' three clusters', va='center', fontdict={'size': 15})
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")

结果：

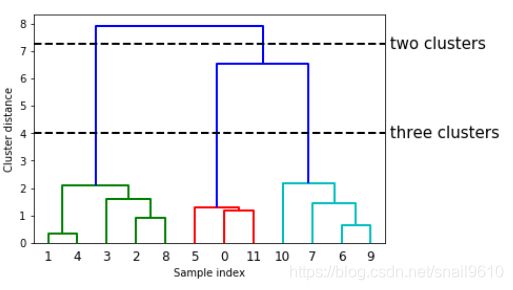
树状图的y 轴不仅说明凝聚算法中两个簇何时合并，每个分支的长度还表示被合并的簇之
间的距离。

3.3 DBSCAN

DBSCAN：density-based spatial clustering of applications with noise，即“具有噪声的基于密度的空间聚类应用”。主要优点：不需要用户先验地设置簇的个数，可以划分具有复杂形状的簇，还可以找出不属于任何簇的点。DBSCAN比凝聚聚类、k均值稍慢，但仍可以扩展到相对较大的数据集。

在某些区域中许多数据点靠近在一起。这些区域被称为特征空间中的密集（dense）区域。DBSCAN 背后的思想是，识别特征空间的“拥挤”区域中的点，簇形成数据的密集区域，并由相对较空的区域分隔开。

DBSCAN有两个参数：min_samples 和eps。如果在距一个给定数据点eps 的距离内至少有min_samples 个数据点，那么这个数据点就是核心样本(core sample，也称核心点)。DBSCAN 将彼此距离小于eps 的核心样本放到同一个簇中。

3.4 聚类算法的对比与评估

1、用真实值评估聚类

有一些指标可用于评估聚类算法相对于真实聚类的结果，其中最重要的是调整rand 指数（adjusted rand index，ARI）和归一化互信息（normalized mutual information，NMI），二者都给出了定量的度量，其最佳值为1，0 表示不相关的聚类（虽然ARI 可以取负值）。

用这种方式评估聚类时，一个常见的错误是使用accuracy_score 而不是adjusted_rand_score、normalized_mutual_info_score 或其他聚类指标。使用精度的问题在于，它要求分配的簇标签与真实值完全匹配。但簇标签本身毫无意义——唯一重要的是哪些点位于同一个簇中。

2、在没有真实值的情况下评估聚类

有一些聚类的评分指标不需要真实值，但它们在实践中的效果并不好。

轮廓系数（silhouette coeffcient） 计算一个簇的紧致度，其值越大越好，最高分数为1。虽然紧致的簇很好，但紧致度不允许复杂的形状。

基于鲁棒性的（robustness-based）聚类指标：先向数据中添加一些噪声，或者使用不同的参数设定，然后运行算法，并对结果进行比较。其思想是，如果许多算法参数和许多数据扰动返回相同的结果，那么它很可能是可信的。

但是，即使我们得到一个鲁棒性很好的聚类或者非常高的轮廓分数，但仍然不知道聚类中是否有任何语义含义，或者聚类是否反映了数据中我们感兴趣的某个方面。要想知道聚类是否对应于我们感兴趣的内容，唯一的办法就是对簇进行人工分析。

4 聚类分析小结

聚类的应用与评估是一个非常定性的过程，通常用在对数据分析的探索。k 均值、DBSCAN 和凝聚聚类算法都可以控制聚类的粒度（granularity）。三种方法都可以用于大型的现实世界数据集，也都可以聚类成多个簇。

k 均值： 可以用簇的平均值来表示簇。它还可以被看作一种分解方法，每个数据点都由其簇中心表示。

凝聚聚类： 可以提供数据的可能划分的整个层次结构，可以通过树状图轻松查看。

中我们感兴趣的某个方面。要想知道聚类是否对应于我们感兴趣的内容，唯一的办法就是对簇进行人工分析。

4 聚类分析小结

聚类的应用与评估是一个非常定性的过程，通常用在对数据分析的探索。k 均值、DBSCAN 和凝聚聚类算法都可以控制聚类的粒度（granularity）。三种方法都可以用于大型的现实世界数据集，也都可以聚类成多个簇。

k 均值： 可以用簇的平均值来表示簇。它还可以被看作一种分解方法，每个数据点都由其簇中心表示。

凝聚聚类： 可以提供数据的可能划分的整个层次结构，可以通过树状图轻松查看。

DBSCAN ： 可以检测到没有分配任何簇的“噪声点”，自动判断簇的数量。允许簇具有复杂的形状。