论文阅读笔记(3)——Translating Embeddings for Modeling Multi-relational Data
- Abstract
- 1 Introduction
-
- Modeling multi-relational data
- Relationships as translations in the embedding space
- 2 Translation-based model
- 3 Related work
- 4 Experiments
-
- 4.1 Data sets
- 4.2 Experimental setup
- 4.3 Link prediction
- 4.4 Learning to predict new relationships with few examples
- 5 Conclusion and future work
Abstract
我们考虑在低维向量空间中嵌入实体和多维数据关系的问题。目标是提出一种易于训练的规范模型,该模型包含数量减少的参数,并且可以扩展到非常大的数据库。因此提出了TransE,一种通过将关系解释为对实体的低维嵌入进行操作的翻译来建模关系的方法。尽管它很简单,但由于大量实验表明TransE在两个知识库的链接预测中明显优于最新方法,因此这种假设被证明是有效的。此外,它可以在具有1M 实体,25k关系和超过17M 训练样本的大规模数据集上成功进行训练。
1 Introduction
多重关系数据是指有向图,其节点对应于表单的实体和边缘(头,标签,尾巴)(表示为(h,l,t)),每一个都表明实体头之间存在名称标签的关系和尾巴。
多重关系数据模型在许多领域起着举足轻重的作用。例:社交网络分析:实体是成员,边(关系)是友谊/社交关系链接,推荐系统:实体是用户和产品,关系是购买,评级,评论或搜索产品。
Modeling multi-relational data
通常,建模过程归结为提取实体之间的局部或全局连接模式,并通过使用这些模式来概括特定实体与所有其他实体之间观察到的关系来执行预测。单一关系的本地性概念可能纯粹是结构性的。与单关系数据相反,在对数据进行描述性分析后可以进行即席而简单的建模假设,而关系数据的困难在于局部性的概念可能同时涉及不同类型的关系和实体,因此多关系数据建模需要更多通用方法,这些方法可以同时考虑所有异构关系来选择适当的模式。
继用户/项目聚类或矩阵分解技术在协作过滤中成功地表示单个关系数据中实体的连通性模式之间的非平凡相似性之后,大多数现有的多关系数据方法都在关系框架内进行了设计。
事实上,即使在复杂且异构的多关系域中,简单而适当的建模假设也可以在准确性和可伸缩性之间取得更好的折衷。
Relationships as translations in the embedding space
本文介绍了TransE,一个基于能量的模型,用于学习实体的低维嵌入。换句话说,关系在嵌入空间中表示为平动:如果(h,l,t)成立,那么尾部实体t的嵌入应该接近头部实体h的嵌入,加上某个依赖于该关系的向量。我们的方法依赖于一组简化的参数,因为它只学习每个实体和每个关系的一个低维向量。
我们基于平移的参数化背后的主要动机是层次关系在KBs中非常常见,而平移是表示它们的自然转换。
新模型的架构主要是为层次结构建模而设计的,在大多数类型的关系上都很强大,并且在真实世界KBs上的链接预测方面可以显著优于最新的方法。此外,它的光参数化使得它能够在包含1M个实体、25k个关系和超过17M个训练样本的Freebase大尺度分割上成功训练。
2 Translation-based model
给定一个由两个实体h, t∈E(实体集)和一个关系l∈L(关系集)组成的三元组(h, l, t)的训练集S,模型学习实体和关系的向量嵌入。嵌入以Rk为值(k是模型的超参数),并以相同的字母表示,以黑体字表示。模型的基本思想:函数关系引发的“l-labeled边缘对应于一个嵌入的翻译,即我们希望h + l ≈ t ,当(h,l,t)满足(t 是h+l的一个最近邻),否则h+l应该远离t。在基于能量的框架下,一个三元组的能量等于d(h + l, t)对于不同的度量d,我们取L1范数或L2范数。
为学习这样的嵌入,对训练集最小化一个基于边缘的排序准则:
L = ∑ ( h , ℓ , t ) ∈ S ∑ ( h ′ , ℓ , t ′ ) ∈ S ( h , ℓ , t ) ′ [ γ + d ( h + ℓ , t ) − d ( h ′ + ℓ , t ′ ) ] + \mathcal{L}=\sum_{(h, \ell, t) \in S} \sum_{\left(h^{\prime}, \ell, t^{\prime}\right) \in S_{(h, \ell, t)}^{\prime}}\left[\gamma+d(\boldsymbol{h}+\ell, \boldsymbol{t})-d\left(\boldsymbol{h}^{\prime}+\boldsymbol{\ell}, \boldsymbol{t}^{\prime}\right)\right]_{+} L=∑(h,ℓ,t)∈S∑(h′,ℓ,t′)∈S(h,ℓ,t)′[γ+d(h+ℓ,t)−d(h′+ℓ,t′)]+ (1)
其中 [x]+为x的正部分,γ > 0为边界超参数,且:
S ( h , ℓ , t ) ′ = { ( h ′ , ℓ , t ) ∣ h ′ ∈ E } ∪ { ( h , ℓ , t ′ ) ∣ t ′ ∈ E } S_{(h, \ell, t)}^{\prime}=\left\{\left(h^{\prime}, \ell, t\right) \mid h^{\prime} \in E\right\} \cup\left\{\left(h, \ell, t^{\prime}\right) \mid t^{\prime} \in E\right\} S(h,ℓ,t)′={(h′,ℓ,t)∣h′∈E}∪{(h,ℓ,t′)∣t′∈E} (2)
根据公式2构造的被破坏的三元集合由训练三元组组成,其中头或尾被一个随机实体替换(但不是同时替换)。损失函数倾向于训练三元组时的能量值比损坏的三元组的能量值更低,因此是预期准则的自然实现。注意,对于给定的实体,当实体作为三个一的头或尾出现时,它的嵌入向量是相同的。
在可能的h、l和t上,通过随机梯度下降(小批量模式)进行优化,附加实体嵌入的L2 -范数为1的约束(对标签嵌入没有正则化或范数约束)。这个约束避免了训练过程通过人为地增加实体嵌入规范来最小化L。
算法1(具体的优化过程):
- 所有实体和关系的嵌入首先按照随机过程进行初始化;
- 在算法的每次主要迭代中,对实体的嵌入向量进行归一化;
- 从训练集中采样一个小的三元组集合,作为小批的训练三元组;
- 对于每一个这样的三元组,我们取样一个损坏的三元组;
- 然后以恒定的学习速率梯度更新参数。
该算法将根据其在验证集上的性能停止。
3 Related work
SE 只是将实体转为向量,关系是一个矩阵,利用矩阵的不可逆性反映关系的不可逆性。距离表达公式是1-norm。
将实体嵌入Rk中,和两个矩阵L1∈Rk×k和L2∈Rk×k,使得d(L1h, L2t)对于损坏的三元组(h,l,t)较大(否则较小)。基本思想:当两个实体属于同一个三元组时,它们的嵌入在某个子空间中应该靠得很近,这取决于它们之间的关系。对头部和尾部使用两种不同的投影矩阵是为了解释可能的不对称关系。SE,以L2为单位矩阵,取L1再现一个平移,则等效为TransE。
神经张量模型 该模型的一个特例对应于表格的学习分数s(h,l,t)(被破坏的三联得分较低):
s ( h , ℓ , t ) = h T L t + ℓ 1 T h + ℓ 2 T t s(h, \ell, t)=\boldsymbol{h}^{T} \boldsymbol{L} \boldsymbol{t}+\boldsymbol{\ell}_{1}^{T} \boldsymbol{h}+\boldsymbol{\ell}_{2}^{T} \boldsymbol{t} s(h,ℓ,t)=hTLt+ℓ1Th+ℓ2Tt (3)
其中L∈Rk×k, L1∈Rk, L2∈Rk,所有这些都取决于l。
以欧几里得距离的平方作为不同函数来考虑TransE,有:
d ( h + ℓ , t ) = ∥ h ∥ 2 2 + ∥ ℓ ∥ 2 2 + ∥ t ∥ 2 2 − 2 ( h T t + ℓ T ( t − h ) ) d(\boldsymbol{h}+\boldsymbol{\ell}, \boldsymbol{t})=\|\boldsymbol{h}\|_{2}^{2}+\|\boldsymbol{\ell}\|_{2}^{2}+\|\boldsymbol{t}\|_{2}^{2}-2\left(\boldsymbol{h}^{T} \boldsymbol{t}+\boldsymbol{\ell}^{T}(\boldsymbol{t}-\boldsymbol{h})\right) d(h+ℓ,t)=∥h∥22+∥ℓ∥22+∥t∥22−2(hTt+ℓT(t−h)) (4)
虽不能用这个模型进行实验(因为它和本文模型是同时发布的),但是TransE的参数要少得多:这可以简化训练,防止拟合不足,并可以弥补较低的表达能力。
TransE的简单表述,可以被视为编码一系列双向交互作用,也存在缺陷。对于建模数据,其中h ,l和t之间的三向依赖是至关重要的,我们的模型可能会失败。例如,在小规模Kinships数据集上,TransE在交叉验证(用精确-回忆曲线下的面积测量)方面的表现无法与最先进的交叉验证相竞争,因为在这种情况下,三元交互至关重要。
4 Experiments
我们的方法TransE是根据从Wordnet和Freebase中提取的数据进行评估的,与文献中最近的几种方法进行对比,这些方法在各种基准测试中获得了最佳的当前性能,并可伸缩到相对大的数据集。
4.1 Data sets
Wordnet 这个知识库旨在生成直观可用的词典和同义词词典,并支持自动文本分析。它的实体(称为synsets)对应于单词的意义,而关系定义了它们之间的词汇关系。
Freebase Freebase是一个庞大且不断增长的知识库;目前大约有12亿三元组和8000多万家实体。我们用Freebase创建了两个数据集。
首先,为了做一个小数据集来进行实验,选择了同样存在于Wikilinks数据库中并且在Freebase中至少有100次提及的实体子集(包括实体和关系)。我们还删除了类似“!”/people/person/nationality’,这只是颠倒了头和尾的关系,而不是/people/person/nationality。结果产生了592,213个三元组,其中有14,951个实体和1,345个关系,这些三元组被随机分割。在本节的其余部分,该数据集为FB15k。
我们还想拥有大规模的数据,以便在规模上测试TransE。因此,通过选择最经常出现的100万个实体,从Freebase创建了另一个数据集。这导致了大约25k的关系和超过1700万的训练三胞胎的分离,称之为FB1M。
4.2 Experimental setup
Evaluation protocol 对于求值,我们使用与[3]相同的排序过程。对于每个测试三元组,头依次被字典的每个实体移除并替换。模型首先计算出这些被破坏的三个一的差异性(或能量),然后按升序进行排序;最终存储正确实体的秩。整个过程重复进行,同时去掉尾巴而不是头。
为避免误导行为,建议从已损坏的三元组列表中删除出现在训练、验证或测试集中的所有三元组(感兴趣的测试三元组除外)。
Baselines 第一种方法是Unstructured,这是TransE的一个版本,它认为数据是单关系的,并将所有转换设置为0。我们还与集体矩阵分解模型RESCAL、基于能量的模型SE、SME(线性)/SME(双线性)和LFM进行了比较。RESCAL通过交替最小二乘方法进行训练,而其他的则通过随机梯度下降(如TransE)进行训练。
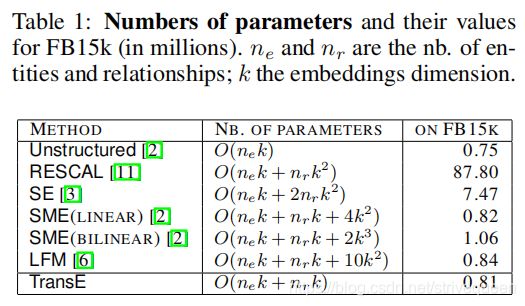
- 对于RESCAL,由于可伸缩性的原因,必须将正则化参数设置为0,并在{50,250,500,1000,2000}中选择潜在维数k,从而得到验证集上的最低平均预测排名(使用raw设置)。
- 对于Unstructured、SE、SME(线性)和SME(双线性),在选择{0.001,0.01,0.1}的学习率,k在{20,50}中。利用验证集上的平均秩(在训练数据上总计最多1000个epoch),通过早期停止选择最佳模型。
- 对于LFM,也使用平均验证等级来选择模型,在{25,50,75}中选择潜在维数,在{50,100,200,500}中选择因子数,在{0.01,0.1,0.5}中选择学习率。
Implementation 对于TransE实验,选择了随机梯度下降法的学习速率λ在{0.001,0.01,0.1},边界γ在{1,2,10},潜在维度k在{20、50}在每个数据集的验证集。不同测量d设置L1和L2距离也根据验证的性能。
在Wordnet上,最优配置为:FB15k:k = 20, p = 0.01, p = 2, d = L1;k = 50, p = 0.01, p = 1, d = L1 ;FB1M:k = 50, pv = 0.01, rr = 1, d = L2。对于所有的数据集,训练时间被限制在训练集的最多1000个epoch。通过早期停止使用验证集(原始设置)上的平均预测秩来选择最佳的模型。
4.3 Link prediction
Overall results TransE在所有指标上都优于所有对手,通常有很大的优势,达到一些有前景的绝对性能得分。
TransE的良好性能是由于根据数据对模型进行了适当的设计,同时也是由于其相对简单。这意味着随机梯度可以有效地优化它。SE比我们的提议更具表现力,但它的复杂性可能使它很难学习,导致性能更差。数据说明,TransE的欠拟合程度确实较低。
当比较TransE和Unstructured(即TransE不带翻译)的性能时,Unstructured的平均等级显得比较好,但hits@10是非常差的。Unstructured只是将所有协作的实体聚在一起,独立于所涉及的关系,因此只能猜测哪些实体是相关的。在FB1M上,TransE和Unstructured的平均排名几乎相似,但TransE在前10名中的排名要高10倍。
如预期一样,预测“一方”的实体似乎更容易(即当多个实体指向它时,预测头:1对多、尾:多对1)。这些是适定的情况。SME(bilinear)在这种情况下被证明是非常精确的,因为它们是那些拥有最多培训实例的。
Unstructured在1对1关系上表现良好:这表明此类关系的参数必须具有共同的隐藏类型,Unstructured可以通过聚集嵌入空间中链接在一起的实体来揭示这些隐藏类型。但这种策略在其他任何类型的关系中都是失败的。添加翻译术语(即将Unstructured升级为TransE)可以在嵌入空间中移动,通过遵循关系从一个实体集群移动到另一个实体集群。
4.4 Learning to predict new relationships with few examples
使用FB15k,我们想要通过检查方法学习新关系的速度来测试方法归纳新事实的能力。

当不提供未知关系的示例时,Unstructured的性能最好,因为它不使用这些信息进行预测。但在提供带标签的示例时,这种性能并没有提高。TransE是最快的学习方法:只用10个新关系的例子,hits@10已经占到18%,并且随着提供的样本数量的增加,它会单调提高。我们相信,TransE模型的简单性使它能够很好地泛化,而不需要修改任何已经训练好的嵌入。
5 Conclusion and future work
提出了一种学习KBs嵌入的新方法,着重于模型的最小参数化,以主要表示层次关系。展示了与两种不同知识库上的竞争方法相比,它工作得非常好,而且是一个高度可伸缩的模型,将它应用于一个非常大的Freebase数据块。虽然还不清楚是否所有的关系类型都可以通过我们的方法充分地建模,通过将评估分成类别(1对1,1对多,…),它似乎表现得很好。