Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shift
Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shift
-
- 一、BatchNormalization的引入
- 二、什么是BatchNormalization
- 三、BN的优点有哪些
- 四、BN的缺点有哪些
- 五、代码实现
BN在神经网络中很常见,BN是什么?为什么要用BN? BN有什么作用?接下来围绕几个点对BN进行总结,并附上BN层forward和backward代码。 正所谓,无总结,不进步。
一、BatchNormalization的引入
1、BN是2015年提出来的,论文题目是:《Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shift》。题目有一个词:internal Covariate Shift,它在原文的意思为that small changes to the network parameters amplify as the network becomes deeper.The change in the distributions of layers’ inputs presents a problem because the layers need to continuously adapt to the new distribution. When the input distribution to a learning system changes, it is said to experience covariate shift.换句话说就是,当网络越来越深的时候,参数的小小改变能使网络产生很大的变化。也就是BN能够降低参数改变带来的变化。
2、若是网络中没有BN,会出现什么问题?
根据求导法则:
![]()
![]()
当W很大的时候,根据链式求导法则,梯度g = g_local * g_out,即本次运算的梯度与前面梯度的乘积,当W小于1的时候,假设W为0.9,经过100层的运算后,梯度为0.9的100次方,是一个很小的值;当W大于1的时候,经过100层的运算,梯度是一个非常大的值,这两种情况分别叫做梯度消失与梯度爆炸。
3、另一方面,对于激活层,有无BN对于激活的影响是什么?
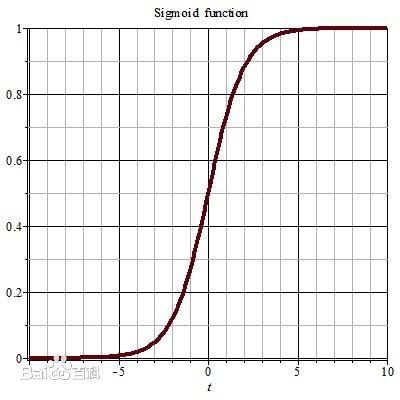
以激活函数sigmoid为例,当数据接近于1或者0的时候,它的曲线是平缓的,也就是梯度会接近于0,当反向传播的时候,梯度几乎是不更新的,网络无法达到训练的目的。文中提到:BN constrain them to the linear regime of the nonlinearity. BN将值从约束到非线性区的相对线性区内,让它们有梯度可以传播。
二、什么是BatchNormalization
根据论文公式,对于m个mini-batch的数据集,先获取该batch的均值和方差,进行normalize,最后进行scale and shift。对于前面三步基本可以看懂,但是最后的scale and shift有什么用,文章中也没有明确说出来。我自己的理解是scale and shift是对归一化后的数据进行偏移和尺度缩放,单一的normalize并不能满足数据分布的要求, scale and shift可以提高数据的信息表达,例如对于激活函数relu,小于0的部分不激活,但是如果数据用了scale and shift,使数据偏移,relu的激活量因此可以得到改变。当然,参数gamma和beta都是网络可以学习的。

Batch Normalization的反向传播,也是用求导的链式法则进行求梯度,求偏导中,loss对xi求偏导,偏导的结果与w无关,可以返回到第一部分提到的梯度消失和梯度爆炸的问题。

三、BN的优点有哪些
1、Batch Normalization enables higher learning rates
large learning rates may increase the scale of layer parameters, which then amplify the gradient during backpropagation and lead to the model explosion. However, with Batch Normalization, back-propagation through a layer is unaffected by the scale of its parameters.
2、Batch Normalization regularizes the model
BN有一定的正则化效果。在每一次的训练中我们用的是mini-batch,用mini-batch的mean和variance来代表整个dataset的mean和variance,虽然用mini-batch是具有代表性的,但是它还不完全是dataset,等于给网络增加了随机噪音。有一定的正则化效果。
3、Accelerating BN Networks
提高了网络的学习速度,每一层的输入数据均值方差在一定的范围内,使下一层网络不必去适应输入的变化,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
4、in some cases eliminating the need for Dropout.
减少对dropout的使用
5、reduce overfitting
降低过拟合,道理同2
四、BN的缺点有哪些
1、效果容易受batch size大小的影响。batch size越大,mini-batch的数据越有代表性,它的mean and variance越接近dataset的mean and variance。但是batch太大,内存不一定够放。
2、难以在RNN中使用,RNN中更多的是使用Layer norm。
五、代码实现
def batchnorm_forward(x, gamma, beta, bn_param):
"""
Forward pass for batch normalization.
During training the sample mean and (uncorrected) sample variance are
computed from minibatch statistics and used to normalize the incoming data.
During training we also keep an exponentially decaying running mean of the
mean and variance of each feature, and these averages are used to normalize
data at test-time.
At each timestep we update the running averages for mean and variance using
an exponential decay based on the momentum parameter:
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
Note that the batch normalization paper suggests a different test-time
behavior: they compute sample mean and variance for each feature using a
large number of training images rather than using a running average. For
this implementation we have chosen to use running averages instead since
they do not require an additional estimation step; the torch7
implementation of batch normalization also uses running averages.
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
#######################################################################
# TODO: Implement the training-time forward pass for batch norm. #
# Use minibatch statistics to compute the mean and variance, use #
# these statistics to normalize the incoming data, and scale and #
# shift the normalized data using gamma and beta. #
# # #
# Note that though you should be keeping track of the running #
# variance, you should normalize the data based on the standard #
# deviation (square root of variance) instead! #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
#######################################################################
sample_mean = np.mean(x, axis=0) #[D]
sample_var = np.var(x, axis=0) #[D]
x_hat = (x - sample_mean) / np.sqrt(sample_var+eps)
out = gamma*x_hat+beta
cache = (gamma, x, sample_mean, sample_var, eps, x_hat) #why is this
#store the global mean and var
running_mean = momentum* running_mean +(1-momentum)*sample_mean
running_var = momentum*running_var+(1-momentum)*sample_var
elif mode == 'test':
#######################################################################
# TODO: Implement the test-time forward pass for batch normalization. #
# Use the running mean and variance to normalize the incoming data, #
# then scale and shift the normalized data using gamma and beta. #
# Store the result in the out variable. #
#######################################################################
scale = gamma / np.sqrt(running_var+eps)
shift = beta- scale*running_mean
out = scale * x + shift
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
def batchnorm_backward(dout, cache):
"""
Backward pass for batch normalization.
For this implementation, you should write out a computation graph for
batch normalization on paper and propagate gradients backward through
intermediate nodes.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from batchnorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
###########################################################################
gamma, x, sample_mean, sample_var, eps, x_hat = cache
N = x.shape[0]
dx_hat = dout * gamma
dvar = np.sum(dx_hat* (x - sample_mean) * -0.5 * np.power(sample_var + eps, -1.5), axis = 0)
dmean = np.sum(dx_hat * -1 / np.sqrt(sample_var +eps), axis = 0) + dvar * np.mean(-2 * (x - sample_mean), axis =0)
dx = 1 / np.sqrt(sample_var + eps) * dx_hat + dvar * 2.0 / N * (x-sample_mean) + 1.0 / N * dmean
dgamma = np.sum(x_hat * dout, axis = 0)
dbeta = np.sum(dout , axis = 0)
return dx, dgamma, dbeta
# test
np.random.seed(231)
N, D = 4, 5
x = 5 * np.random.randn(N, D) + 12
gamma = np.random.randn(D)
beta = np.random.randn(D)
dout = np.random.randn(N, D)
bn_param = {'mode': 'train'}
_, cache = batchnorm_forward(x, gamma, beta, bn_param)
dx, dgamma, dbeta = batchnorm_backward(dout, cache)