kemean
将相似的对象归到同一个簇中,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同数据尽量分离。
K-Means 聚类的步骤如下:
-
随机的选取K个中心点,代表K个类别;
-
计算N个样本点和K个中心点之间的欧氏距离;
-
将每个样本点划分到最近的(欧氏距离最小的)中心点类别中——迭代1;
-
计算每个类别中样本点的均值,得到K个均值,将K个均值作为新的中心点——迭代2;
-
重复步骤2、3、4;
-
满足收敛条件后,得到收敛后的K个中心点(中心点不再变化)。
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()
"""
KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300,
tol=0.0001, precompute_distances='auto', verbose=0,
random_state=None, copy_x=True, n_jobs=1, algorithm='auto')
Parameters:
n_clusters: 聚类个数
max_iter: 最大迭代数
n_init: 用不同的质心初始化值运行算法的次数
init: 初始化质心的方法
precompute_distances:预计算距离
tol: 关于收敛的参数
n_jobs: 计算的进程数
random_state: 随机种子
copy_x:是否修改原始数据
algorithm:“auto”, “full” or “elkan”
”full”就是我们传统的K-Means算法,
“elkan”elkan K-Means算法。默认的
”auto”则会根据数据值是否是稀疏的,来决定如何选择”full”和“elkan”,稠密的选 “elkan”,否则就是”full”
Attributes:
cluster_centers_:质心坐标
Labels_: 每个点的分类
inertia_:每个点到其簇的质心的距离之和。
"""
m_kmeans = KMeans(n_clusters=4)
from sklearn import metrics
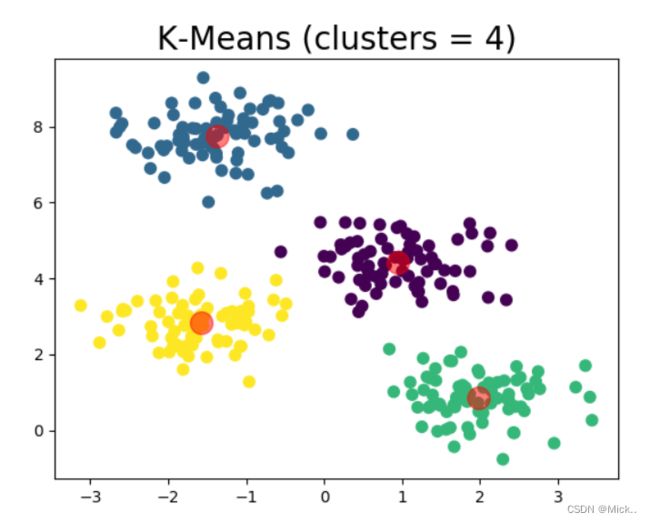
def draw(m_kmeans, X, y_pred, n_clusters):
centers = m_kmeans.cluster_centers_
##质心坐标
print('质心坐标',centers)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
# 中心点(质心)用红色标出
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
print("Calinski-Harabasz score:%lf" % metrics.calinski_harabasz_score(X, y_pred))
plt.title("K-Means (clusters = %d)" % n_clusters, fontsize=20)
plt.show()
m_kmeans.fit(X)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=4, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
y_pred = m_kmeans.predict(X)
draw(m_kmeans, X, y_pred, 4)