机器学习12支持向量机SVM(处理非线性数据)

一、SVM中使用多项式特征

import numpy as np
import matplotlib.pyplot as plt//////from sklearn import datasets
#这里我们不适用真实的数据集，相应的我们使用datasets的另外的功能，来自动生成非线性的数组
x,y=datasets.make_moons()#使用datasets.make_moons()函数来生成数据集//x.shape//y.shape//plt.scatter(x[y==0,0],x[y==0,1])#X[y==0,0],是所有编号为0的X坐标;X[y==0,1]是所有编号为0的Y坐标
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()#这里两个数据集太规则了，我们希望它传入一些扰动

x,y=datasets.make_moons(noise=0.15,random_state=666)#可以把0.15理解成一个标准差,这是一个随机的噪音就要有随机化的影响
#所以还要设置一个random_state其实就是一个随机种子
plt.scatter(x[y==0,0],x[y==0,1])#X[y==0,0],是所有编号为0的X坐标;X[y==0,1]是所有编号为0的Y坐标
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()

from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree,C=1.0):
    return Pipeline(
    [
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("linearSVC",LinearSVC(C=C))
    ]
    )


poly_svc=PolynomialSVC(degree=3)


poly_svc.fit(x,y)


# plot_decision_boundary()函数：绘制模型在二维特征空间的决策边界；
def plot_decision_boundary(model, axis):
    # model：算法模型；
    # axis：区域坐标轴的范围，其中 0,1,2,3 分别对应 x 轴和 y 轴的范围；
    
    # 1）将坐标轴等分为无数的小点，将 x、y 轴分别等分 （坐标轴范围最大值 - 坐标轴范围最小值）*100 份，
    # np.meshgrid()：
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    # np.c_()：
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    # 2）model.predict(X_new)：将分割出的所有的点，都使用模型预测
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    
    # 3）绘制预测结果
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)


plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0,1.5])#x和y的范围的限定
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()

二、使用多项式核函数的SVM

from sklearn.svm import SVC
def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline(
    [
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly",degree=degree,C=C))
    ])

poly_kernel_svc=PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(x,y)


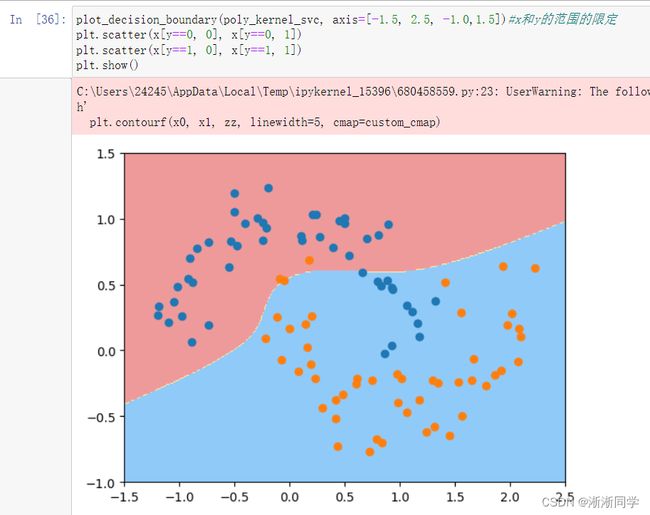
plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0,1.5])#x和y的范围的限定
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()