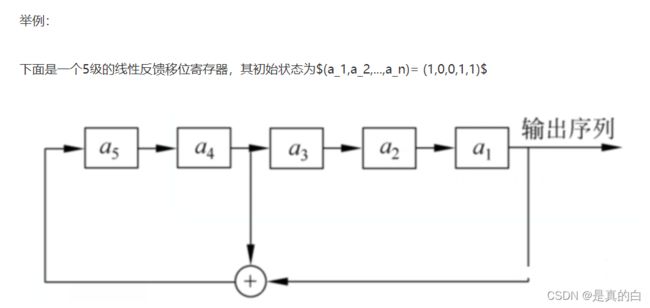
流密码:lfsr(线性反馈移位寄存器)
参考文献:
ctf竞赛密码学之lfsr
ctfwiki crpto lfsr(线性反馈移位寄存器)
简单认识一下lfsr
lfsr可以直接看作下面这个公式,对于我来说还是公式比较好理解,网上很多题解直接对于lfsr函数进行分析,还是没有公式来的舒服,更好理解,我是理解了公式之后才看懂他们在做什么
下面结合具体例题来解释lfsr的逆推方法
2018 强网杯 streamgame1
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==25
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],2)
mask = 0b1010011000100011100
f=open("key","ab")
for i in range(12):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()已知flag是19位得二进制,可以直接爆破
这道题貌似和lfsr没什么关系。。。?
decrypt:
mask = 0b1010011000100011100
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
key=[85,56,247,66,193,13,178,199,237,224,36,58]
for R in range(2**19):
judge=0
for i in range(12):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
if key[i]!=tmp:
judge=1
break
if judge==0:
print(bin(R)[2:])
break
当然这个题可以有另一种更好的做法,对于lfsr可以有更深刻的认识:
key就是flag传入lfsr之后不断生成的序列,也就是我们知道初始值后面的输出序列要逆推初始值
key = 0101010100111000111(只需要取前19位就可)
我们假设我们已经知道了19位,那么我们想要用lfsr求下一位,公式参考上面的公式,得到
a20=a19^a17^a14^a13^a9^a5^a4^a3
刚刚好a19在这个表里,我们可以让a19为唯一未知量来求a19
那么我们把1个未知量放到这个式子里,让其他量已知,我们发现,当flag经过lfsr运算了18次时候符合条件。每一次运算结果都会保存到key里,也就是flag经过的18次lfsr运算都储存到了key里,此时flag还剩下1位,下一次lfsr运算他将被当作a19参加运算,得到a20也就是key[-1]=1
突然明了了,这个时候就只有a19不知道了:
1=$a_{19}$^(R[-3])^(R[-4])^(R[-5])^(R[-9])^(R[-13])^(R[-14])^(R[-17])
a19也就是flag的最后一位求出来了,用这个方法继续往下求直到flag全部求出来
mask = '1010011000100011100' #顺序 c_n,c_n-1,。。。,c_1
key = '0101010100111000111'
R = ''
for i in range(19):
output='x'+key[:18]#我们就是要求这个x
out = int(key[-1])^int(output[-3])^int(output[-4])^int(output[-5])^int(output[-9])^int(output[-13])^int(output[-14])^int(output[-17])
R+=str(out)
key=str(out)+key[:18]
print('flag{'+R[::-1]+'}')2018 强网杯 streamgame2
源码:
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],2)
mask=0x100002
f=open("key","ab")
for i in range(12):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()
弱弱的问一句,这个streamgame1有什么区别吗?
key = '101100101110100100001'
mask= '100000000000000000010'
R = ''
for i in range(21):
output='?'+key[:20]
ans=int(key[-1])^int(output[-2])
R+=str(ans)
key=str(ans)+key[:20]
print(R[::-1])再来看2018 CISCN 初赛 oldstreamgame
原来ctf会遇到这么多一样的题吗!就跟考原题是的
flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
def lfsr(R,mask):
output = (R << 1) & 0xffffffff
i=(R&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100
f=open("key","w")
for i in range(100):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()和上面的同理,貌似也是能爆破的,有兴趣的小伙伴可以尝试一下
decrypt:
import os,sys
os.chdir(sys.path[0])
from Crypto.Util.number import*
key = '00100000111111011110111011111000'#只需要用前32位
mask = '10100100000010000000100010010100'
R = ''
tem = key
for i in range(32):
output = '?' + key[:31]
ans = int(tem[-1-i]) ^ int(output[-3]) ^ int(output[-5]) ^ int(output[-8]) ^ int(output[-12]) ^ int(output[-20]) ^ int(output[-27]) ^ int(output[-30])
R += str(ans)
key = str(ans) + key[:31]
# R = format(int(R[::-1],2),'z')
R = str(hex(int(R[::-1],2))[2:])
print(R)wiki上还给出了一中用矩阵来解的方法,等我学习一下后续补充