2D_Detection-超参
layout: post
title: 2D_Detection-超参
date: 2021-10-04 11:02:51.000000000 +09:00
categories: [算法篇]
tags: [CV, 综述]
mathjax: true
- 前言
- 详细介绍
- learning rate策略
- optimizer
- postive && negative assinger
前言
本文重点介绍深度学习中一些基本参数设置,以及常用的技巧。
详细介绍
learning rate策略
learning rate 的作用是能够在随着深度学习模型逐渐收敛的过程中,控制模型权重更新的“步长”,进一步提升模型精度,基于梯度进行权重更新的基本过程如下:
w e i g h t n e w = w e i g h t e x i s t i n g − l e a r n i n g _ r a t e ∗ f u n c ( g r a d i e n t ) weight_{new} = weight_{existing} - learning\_rate * func(gradient) weightnew=weightexisting−learning_rate∗func(gradient)
下面介绍几种常用的 learning rate 更新策略:
-
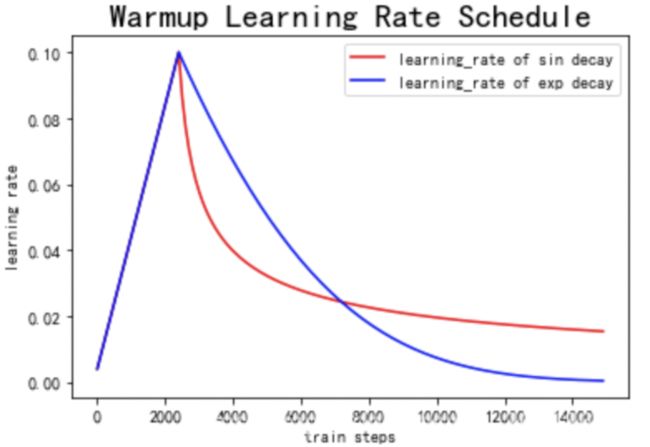
Warmup
Warmup意味着“预热”,其含义是指模型刚开始训练的时候,先用一个比较小的学习率,然后逐渐变大,通过几个epoch的“预热”训练后,再以学习率逐步下降的方式进行模型的正式训练。其出发点在于对非预训练的模型,其权重都是随机的,如果一开始便采用比较大的学习率,那么在训练过程中会增加不确定性。而先采用比较小的学习率,然后慢慢提高,则模型的训练会更加稳定。 -
Decay
Decay策略指的是学习率随着训练step数的增加,学习率下降的策略,简单介绍几种常用的学习率衰减策略:-
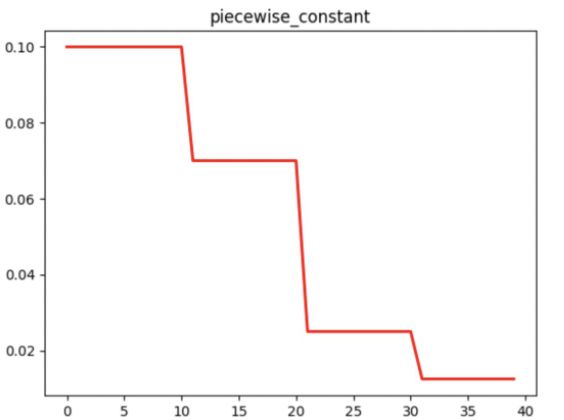
分段衰减:人为设定不同学习率的区间:能够基于不同的任务进行精细的参数调整,可以在任意步长后设定任意数值的
learning rate。 -
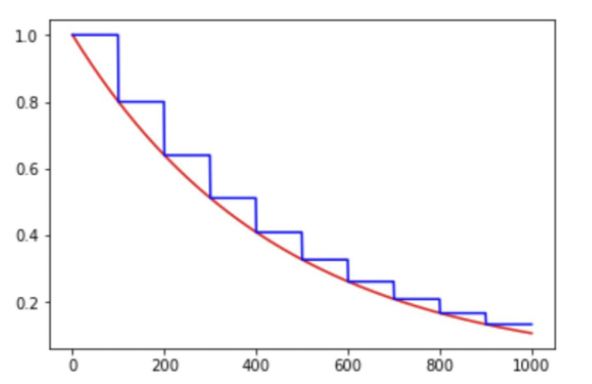
指数衰减:学习率的大小于训练step数存在指数关系:
d e c a y e d _ l e a r n i n g _ r a t e = l e a r n i n g _ r a t e ∗ d e c a y _ r a t e g l o b a l _ s t e p / d e c a y _ s t e p decayed\_learning\_rate = learning\_rate * decay\_rate^{global\_step/decay\_step} decayed_learning_rate=learning_rate∗decay_rateglobal_step/decay_step
-
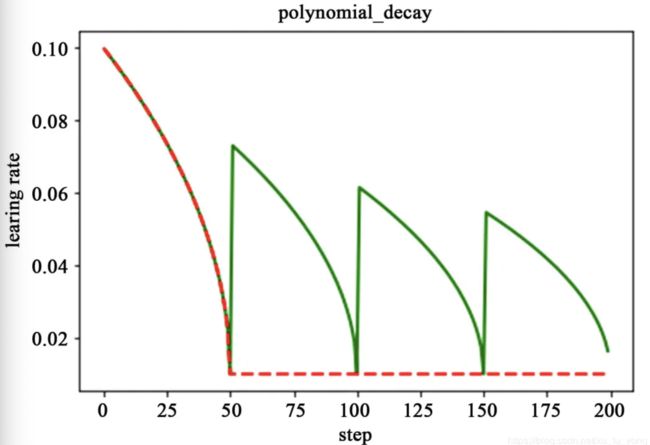
多项式衰减:通过设定初始学习率和最低学习率得到,其更新学习率的方式如下:
g l o b a l _ s t e p = m i n ( g l o b a l _ s t e p , d e c a y _ s t e p ) global\_step = min(global\_step, decay\_step) global_step=min(global_step,decay_step)
d e c a y e d _ l e a r n i n g _ r a t e = ( l e a r n i n g _ r a t e − e n d _ l e a r n i n g _ r a t e ) ∗ ( 1 − g l o b a l _ s t e p d e c a y _ s t e p ) p o w e r + e n d _ l e a r n i n g _ r a t e decayed\_learning\_rate = (learning\_rate - end\_learning\_rate) * (1 - \frac{global\_step}{decay\_step})^{power} + end\_learning\_rate decayed_learning_rate=(learning_rate−end_learning_rate)∗(1−decay_stepglobal_step)power+end_learning_rate
当学习率到达最低值时,存在两种机制:1是保持最小学习率进行更新;2是采用一种循环提高-衰减的学习策略,防止网络局限在局部极小值:
-
余弦衰减:采用余弦相关的方式进行学习率的衰减,其衰减的趋势和余弦函数接近,常见的更新方式如下:
g l o b a l _ s t e p = m i n ( g l o b a l _ s t e p , d e c a y _ s t e p ) global\_step = min(global\_step, decay\_step) global_step=min(global_step,decay_step)
c o s i n e _ d e c a y = 0.5 ∗ ( 1 + c o s ( π ∗ g l o b a l s t e p d e c a y s t e p ) ) cosine\_decay = 0.5 * (1 + cos(\pi * \frac{global_step}{decay_step})) cosine_decay=0.5∗(1+cos(π∗decaystepglobalstep))
d e c a y e d = ( 1 − α ) ∗ ( c o s i n e _ d e c a y ) + α decayed = (1 - \alpha) * (cosine\_decay) + \alpha decayed=(1−α)∗(cosine_decay)+α
d e c a y e d _ l e a r n i n g _ r a t e = l e a r n i n g _ r a t e ∗ d e c a y e d decayed\_learning\_rate = learning\_rate * decayed decayed_learning_rate=learning_rate∗decayed
-
optimizer
optimizer 定义了如何基于得到的梯度和学习率进行权重的更新。以下介绍几种常用的 optimizer :
-
梯度下降法 梯度下降法的计算过程便是:沿着梯度下降方向求解极值,是基本的优化方法。其缺陷是训练速度较慢,且容易陷入局部最优解:
θ t + 1 = θ t − α ∗ Δ θ J ( θ ) \theta _{t+1} = \theta _{t} - \alpha * \Delta _{\theta}J(\theta) θt+1=θt−α∗ΔθJ(θ)
-
动量优化法
动量(Momentum)优化法的思想源于:
物理学上的动量,即物体运动过程中在一定程度上会保持其原先的运动趋势。 对于深度学习中的参数更新来说:参数更新时能够保留之前的更新方向,同时又利用当前的batch进行方向的微调。其优势在于:在梯度方向改变时,能够降低参数更新速度,从而减少震荡;在梯度方向相同时,可以加速参数更新,从而加速收敛。其更新方式如下:
s u m _ o f _ g r a d i e n t = u ∗ g r a d i e n t + p r e v i o u s _ s u m _ o f _ g r a d i e n t ∗ d e c a y _ r a t e sum\_of\_gradient = u * gradient + previous\_sum\_of\_gradient * decay\_rate sum_of_gradient=u∗gradient+previous_sum_of_gradient∗decay_rate
d e l t a = − l e a r n i n g _ r a t e ∗ s u m _ o f _ g r a d i e n t delta = -learning\_rate * sum\_of\_gradient delta=−learning_rate∗sum_of_gradient
t h e t a + = d e l t a theta += delta theta+=delta
-
自适应学习率优化法
前置的
optimizer依赖于超参的设计,如学习率等。自适应学习率优化法则是采用自适应的算法来更新学习率,提高训练过程的适应性。常用的自适应算法有:AdaGrad/RMSProp/Adam等算法。 这里重点介绍下Adam算法,Adam算法同时兼顾了动量和RMSProp算法优点。其参数更新过程如下:先定义初始化参数:全局学习率 σ , 矩估计的指数衰减速率 ρ 1 \rho_1 ρ1/ ρ 2 \rho_2 ρ2, 初始化参数 ω \omega ω,小常数 ε \varepsilon ε;,以及一阶/二阶变量 s s s, r r r,以及时间步计数器 t t t。更新流程如下:
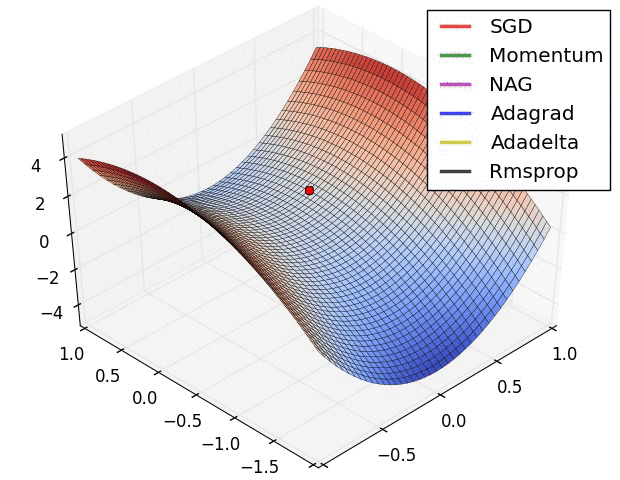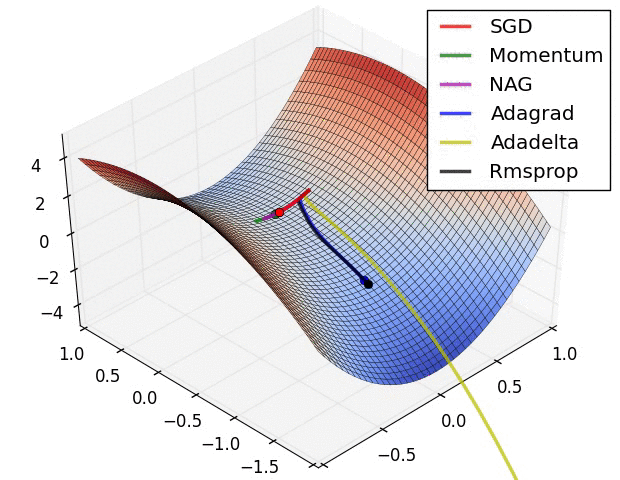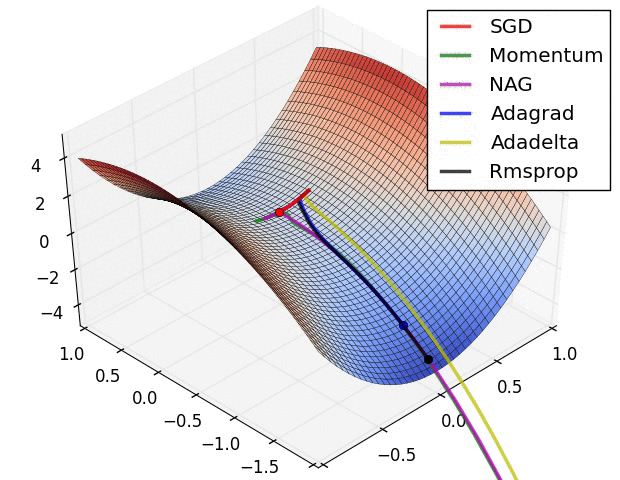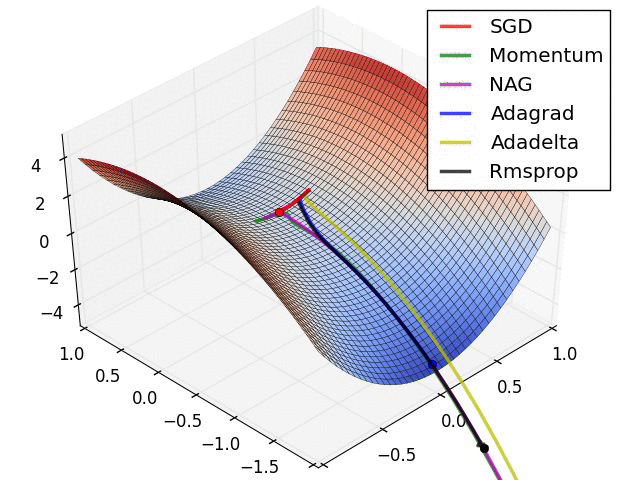
一些经典的 optimizer 对比如下:
postive && negative assinger
对于检测网络来说,正负例样本的分配对于模型训练(尤其指 Anchor-based 检测网络)是十分重要的环节。
前置简单介绍下常规检测网络下基于 Anchor 进行对象匹配和计算 loss :
anchor_generator(基于设置的超参生成anchors)->target_assigner(根据预测的偏移量计算预测框,根据预测框进行正负例分配)->sampler(基于全量正负例进行采样)->loss(根据正负例计算最终的loss,详情参见:2D_Detection-Loss)
简单介绍下 Anchor generator :基于 anchor 预先设置的超参,进行anchor的布置。对于超参来说,常用K-means对训练集进行聚类操作:先完全统计训练集的GT bbox的宽/高,去掉极值点,以均值化区域中心点为初始化点,基于K-Means算法进行优化,优化评价函数为IoU距离。Kmeans聚类anchor简单实现可参考:kmeans。对于 Anchor generator, 大部分网络在 Anchor 生成上都是大同小异的,这里以 SSD/YOLO 为例, SSD 基于 featuremap 各点作为 base anchor 中心点,基于 scale_major 与否,根据 scale/aspect (都是相对值)分布生成大小/长宽比不同的 anchor ,直接回归位置偏移量和尺寸偏移量。 YOLO 的 anchor 生成方式类似与 SSD ,配置方式略有不同,YOLO直接配置Anchor的宽/高。摘录 mmdetection 部分配置:
# SSD
anchor_generator=dict(
type='SSDAnchorGenerator',
scale_major=False,
input_size=input_size,
basesize_ratio_range=(0.15, 0.9),
strides=[8, 16, 32, 64, 100, 300],
ratios=[[2], [2, 3], [2, 3], [2, 3], [2], [2]]),
# YOLO
anchor_generator=dict(
type='YOLOAnchorGenerator',
base_sizes=[[(116, 90), (156, 198), (373, 326)],
[(30, 61), (62, 45), (59, 119)],
[(10, 13), (16, 30), (33, 23)]],
strides=[32, 16, 8]),
在 Target Assigner 和 sampler 层面通常会有比较多的算法设计的技巧。最基本的 Target Assigner 为 Max Iou Assigner :依据IoU进行GT BBox和Predicted BBox的匹配,pipeline为:计算Predicted BBOx和GT BBox的IoU,然后将 bbox assign 为最大IoU的GT(GT和bbox为一对多的关系),再根据阈值赋予正负例。SSD/YOLO等常用网络的Assigner皆为 MaxIouAssigner 。摘录mmdet pipeline:
'''
1. assign every bbox to the background
2. assign proposals whose iou with all gts < neg_iou_thr to 0
3. for each bbox, if the iou with its nearest gt >= pos_iou_thr,
assign it to that bbox
4. for each gt bbox, assign its nearest proposals (may be more than
one) to itself
'''
这里介绍几种比较经典的 Target Assigner 方式:
- MaxIouAssigner_TopK:参考OPMP思路,即单个Anchor match多个GT(TopK),可以实现单个Anchor预测多个结果。
- GridAssigner:YOLO采用的Assigner,与MaxIoUAssigner方式类似,唯一的区别是限制了GT的中心点范围,只赋予中心点在对应格子内的GT为对应格子的target。
- HungarianAssigner:参考OneNet(or Detr)思路,实现gt-bbox的一对一match,采用的
min-cost方式,其中cost通常包含cls loss/bbox loss,匹配方式为匈牙利匹配算法(Hungarian)。 - ATSS:整体pipeline较为复杂:首先计算所有bbox和gt的iou,以及中心点距离;选择中心点最近的k个bbox,计算这些bboxes的mean/std值,以mean+std作为筛选bbox的阈值;取大于阈值的作为pos候选,最后限制候选中心点在对应bbox为正例(如有多个正例则取最大iou的case)。
- 其他:
- FSAF:试图解决不同featuremap层的anchor assigner的问题,方式是:每个feature map层添加一个anchor free branch根据GT在不同层的Loss(Focal Loss+IoU Loss)为GT分配层,从而回归Loss,联合训练则将anchor-based和anchor free层的loss合并。测试过程中则将两者结果合并后做nms。
对于 sampler 来说,其本质上只是采样的过程,通常需要和前置的 Target Assigner 配合,其整体算法设计上比较简单,下面介绍几种常用的 sampler 策略:
- SSD sampler/faster rcnn sampler: SSD sampler的逻辑是先取所有正例case,然后按照pos/neg比例(如1:3)获取负例,其中负例选取采用
hard data mining的策略取loss排序最大的负例。faster rcnn由于second stage的输入batch size固定(256),故一般先取正例,如超出则random sample出需要的正例,剩余为负例,也采用random sample的方式。 - random sampler: 即pos/neg数目大于
expected_num则进行random sample。否则全部返回。 - ohem sampler: 即pos/neg数目大于
expected_num则会前向forward得到对应case的loss取topk(k=expected_num),否则全部返回 - iou_balanced_neg_sampler:出自Libra R-CNN,其正例sample的策略同random sampler,负例sample的策略采用了将负例iou等分bins,然后基于bins进行sample的策略,本质上提高了部分iou区间的sample概率。