高等数学(第七版)同济大学 总习题十 (后10题)个人解答
高等数学(第七版)同济大学 总习题十(后10题)
函数作图软件:Mathematica
7. 设 f ( x , y ) 在 闭 区 域 D = { ( x , y ) ∣ x 2 + y 2 ≤ y , x ≥ 0 } 上 连 续 , 且 f ( x , y ) = 1 − x 2 − y 2 − 8 π ∬ D f ( x , y ) d x d y , 求 f ( x , y ) . \begin{aligned}&7. \ 设f(x, \ y)在闭区域D=\{(x, \ y)\ |\ x^2+y^2 \le y ,x \ge 0\}上连续,且\\\\&\ \ \ \ f(x, \ y)=\sqrt{1-x^2-y^2}-\frac{8}{\pi}\iint_{D}f(x, \ y)dxdy,求f(x, \ y).&\end{aligned} 7. 设f(x, y)在闭区域D={(x, y) ∣ x2+y2≤y,x≥0}上连续,且 f(x, y)=1−x2−y2−π8∬Df(x, y)dxdy,求f(x, y).
解:
设 ∬ D f ( x , y ) d x d y = A , 则 f ( x , y ) = 1 − x 2 − y 2 − 8 π A , 从 而 ∬ D f ( x , y ) d x d y = ∬ D 1 − x 2 − y 2 d x d y − 8 π A ∬ D d x d y , 因 ∬ D d x d y = π 8 , 得 A = ∬ D 1 − x 2 − y 2 d x d y − A , 因 此 A = 1 2 ∬ D 1 − x 2 − y 2 d x d y , 在 极 坐 标 系 中 , D = { ( ρ , θ ) ∣ 0 ≤ ρ ≤ s i n θ , 0 ≤ θ ≤ π 2 } , 因 此 ∬ D 1 − x 2 − y 2 d x d y = ∫ 0 π 2 d θ ∫ 0 s i n θ 1 − ρ 2 ρ d ρ = π 6 − 2 9 , 得 A = π 12 − 1 9 , 则 f ( x , y ) = 1 − x 2 − y 2 + 8 9 π − 2 3 . \begin{aligned} &\ \ 设\iint_{D}f(x, \ y)dxdy=A,则f(x, \ y)=\sqrt{1-x^2-y^2}-\frac{8}{\pi}A,从而\\\\ &\ \ \iint_{D}f(x, \ y)dxdy=\iint_{D}\sqrt{1-x^2-y^2}dxdy-\frac{8}{\pi}A\iint_{D}dxdy,因\iint_{D}dxdy=\frac{\pi}{8},\\\\ &\ \ 得A=\iint_{D}\sqrt{1-x^2-y^2}dxdy-A,因此A=\frac{1}{2}\iint_{D}\sqrt{1-x^2-y^2}dxdy,在极坐标系中,\\\\ &\ \ D=\{(\rho, \ \theta)\ |\ 0 \le \rho \le sin\ \theta,0 \le \theta \le \frac{\pi}{2}\},因此\iint_{D}\sqrt{1-x^2-y^2}dxdy=\int_{0}^{\frac{\pi}{2}}d\theta \int_{0}^{sin\ \theta}\sqrt{1-\rho^2}\rho d\rho=\frac{\pi}{6}-\frac{2}{9},\\\\ &\ \ 得A=\frac{\pi}{12}-\frac{1}{9},则f(x, \ y)=\sqrt{1-x^2-y^2}+\frac{8}{9\pi}-\frac{2}{3}. & \end{aligned} 设∬Df(x, y)dxdy=A,则f(x, y)=1−x2−y2−π8A,从而 ∬Df(x, y)dxdy=∬D1−x2−y2dxdy−π8A∬Ddxdy,因∬Ddxdy=8π, 得A=∬D1−x2−y2dxdy−A,因此A=21∬D1−x2−y2dxdy,在极坐标系中, D={(ρ, θ) ∣ 0≤ρ≤sin θ,0≤θ≤2π},因此∬D1−x2−y2dxdy=∫02πdθ∫0sin θ1−ρ2ρdρ=6π−92, 得A=12π−91,则f(x, y)=1−x2−y2+9π8−32.
8. 把 积 分 ∭ Ω f ( x , y , z ) d x d y d z 化 为 三 次 积 分 , 其 中 积 分 区 域 Ω 是 由 曲 面 z = x 2 + y 2 , y = x 2 及 平 面 y = 1 , z = 0 所 围 成 的 闭 区 域 . \begin{aligned}&8. \ 把积分\iiint_{\Omega}f(x, \ y, \ z)dxdydz化为三次积分,其中积分区域\Omega是由曲面z=x^2+y^2,y=x^2及平面\\\\&\ \ \ \ y=1,z=0所围成的闭区域.&\end{aligned} 8. 把积分∭Ωf(x, y, z)dxdydz化为三次积分,其中积分区域Ω是由曲面z=x2+y2,y=x2及平面 y=1,z=0所围成的闭区域.
解:
Ω 为 曲 顶 柱 体 , 顶 为 z = x 2 + y 2 , 底 位 于 x O y 面 上 , 侧 面 由 抛 物 柱 面 y = x 2 及 平 面 y = 1 所 组 成 , 可 知 Ω 在 x O y 面 上 的 投 影 区 域 D x y = { ( x , y ) ∣ x 2 ≤ y ≤ 1 , − 1 ≤ x ≤ 1 } , 因 此 ∭ Ω f ( x , y , z ) d x d y d z = ∬ D x y d x d y ∫ 0 x 2 + y 2 f ( x , y , z ) d z = ∫ − 1 1 d x ∫ x 2 1 d y ∫ 0 x 2 + y 2 f ( x , y , z ) d z . \begin{aligned} &\ \ \Omega为曲顶柱体,顶为z=x^2+y^2,底位于xOy面上,侧面由抛物柱面y=x^2及平面y=1所组成,可知\Omega在xOy面上的\\\\ &\ \ 投影区域D_{xy}=\{(x, \ y)\ |\ x^2 \le y \le 1,-1 \le x \le 1\},因此\iiint_{\Omega}f(x, \ y, \ z)dxdydz=\\\\ &\ \ \iint_{D_{xy}}dxdy\int_{0}^{x^2+y^2}f(x, \ y, \ z)dz=\int_{-1}^{1}dx\int_{x^2}^{1}dy\int_{0}^{x^2+y^2}f(x, \ y, \ z)dz. & \end{aligned} Ω为曲顶柱体,顶为z=x2+y2,底位于xOy面上,侧面由抛物柱面y=x2及平面y=1所组成,可知Ω在xOy面上的 投影区域Dxy={(x, y) ∣ x2≤y≤1,−1≤x≤1},因此∭Ωf(x, y, z)dxdydz= ∬Dxydxdy∫0x2+y2f(x, y, z)dz=∫−11dx∫x21dy∫0x2+y2f(x, y, z)dz.
9. 计 算 下 列 三 重 积 分 : \begin{aligned}&9. \ 计算下列三重积分:&\end{aligned} 9. 计算下列三重积分:
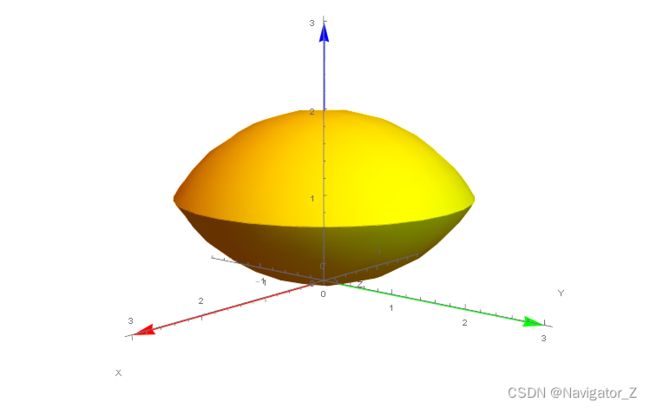
( 1 ) ∭ Ω z 2 d x d y d z , 其 中 Ω 是 两 个 球 ; x 2 + y 2 + z 2 ≤ R 2 和 x 2 + y 2 + z 2 ≤ 2 R z ( R > 0 ) 的 公 共 部 分 ; ( 2 ) ∭ Ω z l n ( x 2 + y 2 + z 2 + 1 ) x 2 + y 2 + z 2 + 1 d v , 其 中 Ω 是 由 球 面 x 2 + y 2 + z 2 = 1 所 围 成 的 闭 区 域 ; ( 3 ) ∭ Ω ( y 2 + z 2 ) d v , 其 中 Ω 是 由 x O y 平 面 上 曲 线 y 2 = 2 x 绕 x 轴 旋 转 而 成 的 曲 面 与 平 面 x = 5 所 围 成 的 闭 区 域 . \begin{aligned} &\ \ (1)\ \ \iiint_{\Omega}z^2dxdydz,其中\Omega是两个球;x^2+y^2+z^2 \le R^2和x^2+y^2+z^2 \le 2Rz\ (R \gt 0)的公共部分;\\\\ &\ \ (2)\ \ \iiint_{\Omega}\frac{zln(x^2+y^2+z^2+1)}{x^2+y^2+z^2+1}dv,其中\Omega是由球面x^2+y^2+z^2=1所围成的闭区域;\\\\ &\ \ (3)\ \ \iiint_{\Omega}(y^2+z^2)dv,其中\Omega是由xOy平面上曲线y^2=2x绕x轴旋转而成的曲面与平面x=5所围成的闭区域. & \end{aligned} (1) ∭Ωz2dxdydz,其中Ω是两个球;x2+y2+z2≤R2和x2+y2+z2≤2Rz (R>0)的公共部分; (2) ∭Ωx2+y2+z2+1zln(x2+y2+z2+1)dv,其中Ω是由球面x2+y2+z2=1所围成的闭区域; (3) ∭Ω(y2+z2)dv,其中Ω是由xOy平面上曲线y2=2x绕x轴旋转而成的曲面与平面x=5所围成的闭区域.
解:
( 1 ) 利 用 直 角 坐 标 系 , 由 { x 2 + y 2 + z 2 = R 2 , x 2 + y 2 + z 2 = 2 R z 得 z = R 2 , 用 平 面 z = R 2 把 Ω 分 为 两 部 分 , 其 中 Ω 1 = { ( x , y , z ) ∣ x 2 + y 2 ≤ 2 R z − z 2 , 0 ≤ z ≤ R 2 } , Ω 2 = { ( x , y , z ) ∣ x + y 2 ≤ R 2 − z 2 , R 2 ≤ z ≤ R } , 则 ∭ Ω z 2 d x d y d z = ∭ Ω 1 z 2 d x d y d z + ∭ Ω 2 z 2 d x d y d z = ∫ 0 R 2 z 2 d z ∬ x 2 + y 2 ≤ 2 R z − z 2 d x d y + ∫ R 2 R z 2 d z ∬ x 2 + y 2 ≤ R 2 − z 2 d x d y = ∫ 0 R 2 π ( 2 R z − z 2 ) ⋅ z 2 d z + ∫ R 2 R π ( R 2 − z 2 ) ⋅ z 2 d z = 1 40 π R 5 + 47 480 π R 5 = 59 480 π R 5 . \begin{aligned} &\ \ (1)\ 利用直角坐标系,由\begin{cases}x^2+y^2+z^2=R^2,\\\\x^2+y^2+z^2=2Rz\end{cases}得z=\frac{R}{2},用平面z=\frac{R}{2}把\Omega分为两部分,其中\\\\ &\ \ \ \ \ \ \ \ \Omega_1=\left\{(x, \ y, \ z)\ \bigg|\ x^2+y^2 \le 2Rz-z^2,0 \le z \le \frac{R}{2}\right\},\Omega_2=\left\{(x, \ y, \ z)\ \bigg|\ x^+y^2 \le R^2-z^2,\frac{R}{2} \le z \le R\right\},则\\\\ &\ \ \ \ \ \ \ \ \iiint_{\Omega}z^2dxdydz=\iiint_{\Omega_1}z^2dxdydz+\iiint_{\Omega_2}z^2dxdydz=\\\\ &\ \ \ \ \ \ \ \ \int_{0}^{\frac{R}{2}}z^2dz\iint_{x^2+y^2 \le 2Rz-z^2}dxdy+\int_{\frac{R}{2}}^{R}z^2dz\iint_{x^2+y^2 \le R^2-z^2}dxdy=\int_{0}^{\frac{R}{2}}\pi(2Rz-z^2)\cdot z^2dz+\int_{\frac{R}{2}}^{R}\pi(R^2-z^2)\cdot z^2 dz=\\\\ &\ \ \ \ \ \ \ \ \frac{1}{40}\pi R^5+\frac{47}{480}\pi R^5=\frac{59}{480}\pi R^5. & \end{aligned} (1) 利用直角坐标系,由⎩⎪⎨⎪⎧x2+y2+z2=R2,x2+y2+z2=2Rz得z=2R,用平面z=2R把Ω分为两部分,其中 Ω1={(x, y, z) ∣∣∣∣ x2+y2≤2Rz−z2,0≤z≤2R},Ω2={(x, y, z) ∣∣∣∣ x+y2≤R2−z2,2R≤z≤R},则 ∭Ωz2dxdydz=∭Ω1z2dxdydz+∭Ω2z2dxdydz= ∫02Rz2dz∬x2+y2≤2Rz−z2dxdy+∫2RRz2dz∬x2+y2≤R2−z2dxdy=∫02Rπ(2Rz−z2)⋅z2dz+∫2RRπ(R2−z2)⋅z2dz= 401πR5+48047πR5=48059πR5.
( 2 ) 因 为 积 分 区 域 Ω 关 于 x O y 面 对 称 , 被 积 函 数 关 于 z 是 奇 函 数 , 所 以 , 所 求 积 分 为 0. ( 3 ) 积 分 区 域 Ω 由 旋 转 抛 物 面 y 2 + z 2 = 2 x 和 平 面 x = 5 所 围 成 , Ω 在 y O z 面 上 的 投 影 区 域 D y z = { ( y , z ) ∣ y 2 + z 2 ≤ 10 } , Ω 表 示 为 1 2 ( y 2 + z 2 ) ≤ x ≤ 5 , 0 ≤ y 2 + z 2 ≤ 10 , 则 ∭ Ω ( y 2 + z 2 ) d v = ∬ D y z ( y 2 + z 2 ) d y d z ∫ y 2 + z 2 2 5 d x = ∬ D y z ( y 2 + z 2 ) ( 5 − y 2 + z 2 2 ) d y d z 极 坐 标 ‾ ‾ ∬ D y z ρ 2 ( 5 − ρ 2 2 ) ρ d ρ d θ = ∫ 0 2 π d θ ∫ 0 10 ρ 3 ( 5 − ρ 2 2 ) d ρ = 250 3 π . \begin{aligned} &\ \ (2)\ 因为积分区域\Omega关于xOy面对称,被积函数关于z是奇函数,所以,所求积分为0.\\\\ &\ \ (3)\ 积分区域\Omega由旋转抛物面y^2+z^2=2x和平面x=5所围成,\Omega在yOz面上的投影区域\\\\ &\ \ \ \ \ \ \ \ D_{yz}=\{(y, \ z)\ |\ y^2+z^2 \le 10\},\Omega表示为\frac{1}{2}(y^2+z^2) \le x \le 5,0 \le y^2+z^2 \le 10,\\\\ &\ \ \ \ \ \ \ \ 则\iiint_{\Omega}(y^2+z^2)dv=\iint_{D_{yz}}(y^2+z^2)dydz\int_{\frac{y^2+z^2}{2}}^{5}dx=\\\\ &\ \ \ \ \ \ \ \ \iint_{D_{yz}}(y^2+z^2)\left(5-\frac{y^2+z^2}{2}\right)dydz\underline{\underline{极坐标}}\iint_{D_{yz}}\rho^2\left(5-\frac{\rho^2}{2}\right)\rho d\rho d\theta=\int_{0}^{2\pi}d\theta \int_{0}^{\sqrt{10}}\rho^3\left(5-\frac{\rho^2}{2}\right)d\rho=\frac{250}{3}\pi. & \end{aligned} (2) 因为积分区域Ω关于xOy面对称,被积函数关于z是奇函数,所以,所求积分为0. (3) 积分区域Ω由旋转抛物面y2+z2=2x和平面x=5所围成,Ω在yOz面上的投影区域 Dyz={(y, z) ∣ y2+z2≤10},Ω表示为21(y2+z2)≤x≤5,0≤y2+z2≤10, 则∭Ω(y2+z2)dv=∬Dyz(y2+z2)dydz∫2y2+z25dx= ∬Dyz(y2+z2)(5−2y2+z2)dydz极坐标∬Dyzρ2(5−2ρ2)ρdρdθ=∫02πdθ∫010ρ3(5−2ρ2)dρ=3250π.
10. 设 函 数 f ( x ) 连 续 且 恒 大 于 零 , F ( t ) = ∭ Ω ( t ) f ( x 2 + y 2 + z 2 ) d v ∬ D ( t ) f ( x 2 + y 2 ) d σ , G ( t ) = ∬ D ( t ) f ( x 2 + y 2 ) d σ ∫ − t t f ( x 2 ) d x , 其 中 Ω ( t ) = { ( x , y , z ) ∣ x 2 + y 2 + z 2 ≤ t 2 } , D ( t ) = { ( x , y ) ∣ x 2 + y 2 ≤ t 2 } . \begin{aligned}&10. \ 设函数f(x)连续且恒大于零,F(t)=\frac{\iiint_{\Omega(t)}f(x^2+y^2+z^2)dv}{\iint_{D(t)}f(x^2+y^2)d\sigma},G(t)=\frac{\iint_{D(t)}f(x^2+y^2)d\sigma}{\int_{-t}^{t}f(x^2)dx},其中\\\\&\ \ \ \ \ \ \Omega(t)=\{(x, \ y, \ z)\ |\ x^2+y^2+z^2 \le t^2\},D(t)=\{(x, \ y)\ |\ x^2+y^2 \le t^2\}.&\end{aligned} 10. 设函数f(x)连续且恒大于零,F(t)=∬D(t)f(x2+y2)dσ∭Ω(t)f(x2+y2+z2)dv,G(t)=∫−ttf(x2)dx∬D(t)f(x2+y2)dσ,其中 Ω(t)={(x, y, z) ∣ x2+y2+z2≤t2},D(t)={(x, y) ∣ x2+y2≤t2}.
( 1 ) 讨 论 F ( t ) 在 区 间 ( 0 , + ∞ ) 内 的 单 调 性 ; ( 2 ) 证 明 当 t > 0 时 , F ( t ) > 2 π G ( t ) . \begin{aligned} &\ \ (1)\ \ 讨论F(t)在区间(0, \ +\infty)内的单调性;\\\\ &\ \ (2)\ \ 证明当t \gt 0时,F(t) \gt \frac{2}{\pi}G(t). & \end{aligned} (1) 讨论F(t)在区间(0, +∞)内的单调性; (2) 证明当t>0时,F(t)>π2G(t).
解:
( 1 ) 利 用 球 面 坐 标 , ∭ Ω ( t ) f ( x 2 + y 2 + z 2 ) d v = ∫ 0 2 π d θ ∫ 0 π s i n φ d φ ∫ 0 t f ( r 2 ) r 2 d r = 4 π ∫ 0 t f ( r 2 ) r 2 d r , 利 用 极 坐 标 , ∬ D ( t ) f ( x 2 + y 2 ) d σ = ∫ 0 2 π d θ ∫ 0 t f ( ρ 2 ) ρ d ρ = 2 π ∫ 0 t f ( ρ 2 ) ρ d ρ = 2 π ∫ 0 t f ( r 2 ) r d r , 则 F ( t ) = 2 ∫ 0 t f ( r 2 ) r 2 d r ∫ 0 t f ( r 2 ) r d r , F ′ ( t ) = 2 t f ( t 2 ) ∫ 0 t f ( r 2 ) r ( t − r ) d r [ ∫ 0 t f ( r 2 ) r d r ] 2 , 所 以 在 区 间 ( 0 , + ∞ ) 内 , F ′ ( t ) > 0 , 所 以 F ( t ) 在 ( 0 , + ∞ ) 内 单 调 增 加 . ( 2 ) 因 为 f ( x 2 ) 是 偶 函 数 , 所 以 ∫ − t t f ( x 2 ) d x = 2 ∫ 0 t f ( x 2 ) d x = 2 ∫ 0 t f ( r 2 ) d r , 则 G ( t ) = ∫ 0 2 π d θ ∫ 0 t f ( r 2 ) r d r 2 ∫ 0 t f ( r 2 ) d r = π ∫ 0 t f ( r 2 ) r d r ∫ 0 t f ( r 2 ) d r , 证 明 t > 0 时 , F ( t ) > 2 π G ( t ) , 即 证 2 ∫ 0 t f ( r 2 ) r 2 d r ∫ 0 t f ( r 2 ) r d r > 2 ∫ 0 t f ( r 2 ) r d r ∫ 0 t f ( r 2 ) d r , 只 需 证 当 t > 0 时 , H ( t ) = ∫ 0 t f ( r 2 ) r 2 d r ⋅ ∫ 0 t f ( r 2 ) d r − [ ∫ 0 t f ( r 2 ) r d r ] 2 > 0 , 因 为 H ( 0 ) = 0 , H ′ ( t ) = f ( t 2 ) ∫ 0 t f ( r 2 ) ( t − r ) 2 d r > 0 , 所 以 H ( t ) 在 ( 0 , + ∞ ) 内 单 调 增 加 , 又 因 H ( t ) 在 [ 0 , + ∞ ) 上 连 续 , 则 当 t > 0 时 , H ( t ) > H ( 0 ) = 0 , 因 此 当 t > 0 时 , 有 F ( t ) > 2 π G ( t ) . \begin{aligned} &\ \ (1)\ 利用球面坐标,\iiint_{\Omega(t)}f(x^2+y^2+z^2)dv=\int_{0}^{2\pi}d\theta \int_{0}^{\pi}sin\ \varphi d\varphi\int_{0}^{t}f(r^2)r^2dr=4\pi \int_{0}^{t}f(r^2)r^2dr,\\\\ &\ \ \ \ \ \ \ \ 利用极坐标,\iint_{D(t)}f(x^2+y^2)d\sigma=\int_{0}^{2\pi}d\theta \int_{0}^{t}f(\rho^2)\rho d\rho=2\pi \int_{0}^{t}f(\rho^2)\rho d\rho=2\pi \int_{0}^{t}f(r^2)rdr,\\\\ &\ \ \ \ \ \ \ \ 则F(t)=\frac{2\int_{0}^{t}f(r^2)r^2dr}{\int_{0}^{t}f(r^2)rdr},F'(t)=\frac{2tf(t^2)\int_{0}^{t}f(r^2)r(t-r)dr}{\left[\int_{0}^{t}f(r^2)rdr\right]^2},\\\\ &\ \ \ \ \ \ \ \ 所以在区间(0, \ +\infty)内,F'(t) \gt 0,所以F(t)在(0, \ +\infty)内单调增加.\\\\ &\ \ (2)\ 因为f(x^2)是偶函数,所以\int_{-t}^{t}f(x^2)dx=2\int_{0}^{t}f(x^2)dx=2\int_{0}^{t}f(r^2)dr,则\\\\ &\ \ \ \ \ \ \ \ G(t)=\frac{\int_{0}^{2\pi}d\theta \int_{0}^{t}f(r^2)rdr}{2\int_{0}^{t}f(r^2)dr}=\frac{\pi \int_{0}^{t}f(r^2)rdr}{\int_{0}^{t}f(r^2)dr},证明t \gt 0 时,F(t) \gt \frac{2}{\pi}G(t),即证\frac{2\int_{0}^{t}f(r^2)r^2dr}{\int_{0}^{t}f(r^2)rdr} \gt \frac{2\int_{0}^{t}f(r^2)rdr}{\int_{0}^{t}f(r^2)dr},\\\\ &\ \ \ \ \ \ \ \ 只需证当t \gt 0时,H(t)=\int_{0}^{t}f(r^2)r^2dr \cdot \int_{0}^{t}f(r^2)dr-\left[\int_{0}^{t}f(r^2)rdr\right]^2 \gt 0,因为H(0)=0,\\\\ &\ \ \ \ \ \ \ \ H'(t)=f(t^2)\int_{0}^{t}f(r^2)(t-r)^2dr \gt 0,所以H(t)在(0, \ +\infty)内单调增加,又因H(t)在[0, \ +\infty)上连续,\\\\ &\ \ \ \ \ \ \ \ 则当t \gt 0时,H(t) \gt H(0)=0,因此当t \gt 0时,有F(t) \gt \frac{2}{\pi}G(t). & \end{aligned} (1) 利用球面坐标,∭Ω(t)f(x2+y2+z2)dv=∫02πdθ∫0πsin φdφ∫0tf(r2)r2dr=4π∫0tf(r2)r2dr, 利用极坐标,∬D(t)f(x2+y2)dσ=∫02πdθ∫0tf(ρ2)ρdρ=2π∫0tf(ρ2)ρdρ=2π∫0tf(r2)rdr, 则F(t)=∫0tf(r2)rdr2∫0tf(r2)r2dr,F′(t)=[∫0tf(r2)rdr]22tf(t2)∫0tf(r2)r(t−r)dr, 所以在区间(0, +∞)内,F′(t)>0,所以F(t)在(0, +∞)内单调增加. (2) 因为f(x2)是偶函数,所以∫−ttf(x2)dx=2∫0tf(x2)dx=2∫0tf(r2)dr,则 G(t)=2∫0tf(r2)dr∫02πdθ∫0tf(r2)rdr=∫0tf(r2)drπ∫0tf(r2)rdr,证明t>0时,F(t)>π2G(t),即证∫0tf(r2)rdr2∫0tf(r2)r2dr>∫0tf(r2)dr2∫0tf(r2)rdr, 只需证当t>0时,H(t)=∫0tf(r2)r2dr⋅∫0tf(r2)dr−[∫0tf(r2)rdr]2>0,因为H(0)=0, H′(t)=f(t2)∫0tf(r2)(t−r)2dr>0,所以H(t)在(0, +∞)内单调增加,又因H(t)在[0, +∞)上连续, 则当t>0时,H(t)>H(0)=0,因此当t>0时,有F(t)>π2G(t).
11. 求 平 面 x a + y b + z c = 1 被 三 坐 标 面 所 割 出 的 有 限 部 分 的 面 积 . \begin{aligned}&11. \ 求平面\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1被三坐标面所割出的有限部分的面积.&\end{aligned} 11. 求平面ax+by+cz=1被三坐标面所割出的有限部分的面积.
解:
平 面 方 程 为 z = c − c a x − c b y , 被 三 坐 标 面 割 出 的 有 限 部 分 在 x O y 面 上 的 投 影 区 域 D x y 为 x 轴 、 y 轴 和 直 线 x a + y b = 1 所 围 成 的 三 角 形 区 域 , 所 求 面 积 为 A = ∬ D x y 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d x d y = ∬ D x y 1 + c 2 a 2 + c 2 b 2 d x d y = 1 ∣ a b ∣ a 2 b 2 + b 2 c 2 + c 2 a 2 ∭ D x y d x d y = 1 ∣ a b ∣ a 2 b 2 + b 2 c 2 + c 2 a 2 ⋅ 1 2 ∣ a b ∣ = 1 2 a 2 b 2 + b 2 c 2 + c 2 a 2 . \begin{aligned} &\ \ 平面方程为z=c-\frac{c}{a}x-\frac{c}{b}y,被三坐标面割出的有限部分在xOy面上的投影区域D_{xy}为x轴、y轴和直线\frac{x}{a}+\frac{y}{b}=1\\\\ &\ \ 所围成的三角形区域,所求面积为A=\iint_{D_{xy}}\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}dxdy=\iint_{D_{xy}}\sqrt{1+\frac{c^2}{a^2}+\frac{c^2}{b^2}}dxdy=\\\\ &\ \ \frac{1}{|ab|}\sqrt{a^2b^2+b^2c^2+c^2a^2}\iiint_{D_{xy}}dxdy=\frac{1}{|ab|}\sqrt{a^2b^2+b^2c^2+c^2a^2}\cdot \frac{1}{2}|ab|=\frac{1}{2}\sqrt{a^2b^2+b^2c^2+c^2a^2}. & \end{aligned} 平面方程为z=c−acx−bcy,被三坐标面割出的有限部分在xOy面上的投影区域Dxy为x轴、y轴和直线ax+by=1 所围成的三角形区域,所求面积为A=∬Dxy1+(∂x∂z)2+(∂y∂z)2dxdy=∬Dxy1+a2c2+b2c2dxdy= ∣ab∣1a2b2+b2c2+c2a2∭Dxydxdy=∣ab∣1a2b2+b2c2+c2a2⋅21∣ab∣=21a2b2+b2c2+c2a2.
12. 在 均 匀 的 半 径 为 R 的 半 圆 形 薄 片 的 直 径 上 , 要 接 上 一 个 一 边 与 直 径 等 长 的 同 样 材 料 的 均 匀 矩 形 薄 片 , 为 了 使 整 个 均 匀 薄 片 的 质 心 恰 好 落 在 圆 心 上 , 问 接 上 去 的 均 匀 矩 形 薄 片 另 一 边 的 长 度 应 是 多 少 ? \begin{aligned}&12. \ 在均匀的半径为R的半圆形薄片的直径上,要接上一个一边与直径等长的同样材料的均匀矩形薄片,\\\\&\ \ \ \ \ \ 为了使整个均匀薄片的质心恰好落在圆心上,问接上去的均匀矩形薄片另一边的长度应是多少?&\end{aligned} 12. 在均匀的半径为R的半圆形薄片的直径上,要接上一个一边与直径等长的同样材料的均匀矩形薄片, 为了使整个均匀薄片的质心恰好落在圆心上,问接上去的均匀矩形薄片另一边的长度应是多少?
解:
设 矩 形 另 一 边 的 长 度 为 l , 建 立 直 角 坐 标 , 质 心 的 纵 标 y ‾ = ∬ D y d σ A = ∫ − R R d x ∫ − l R 2 − x 2 y d y A = ∫ − R R ( R 2 − x 2 − l 2 ) d x 2 A = 2 3 R 3 − l 2 R A , 因 为 y ‾ = 0 , 得 l = 2 3 R . \begin{aligned} &\ \ 设矩形另一边的长度为l,建立直角坐标,质心的纵标\overline{y}=\frac{\iint_{D}yd\sigma}{A}=\frac{\int_{-R}^{R}dx\int_{-l}^{\sqrt{R^2-x^2}}ydy}{A}=\frac{\int_{-R}^{R}(R^2-x^2-l^2)dx}{2A}=\\\\ &\ \ \frac{\frac{2}{3}R^3-l^2R}{A},因为\overline{y}=0,得l=\sqrt{\frac{2}{3}}R. & \end{aligned} 设矩形另一边的长度为l,建立直角坐标,质心的纵标y=A∬Dydσ=A∫−RRdx∫−lR2−x2ydy=2A∫−RR(R2−x2−l2)dx= A32R3−l2R,因为y=0,得l=32R.
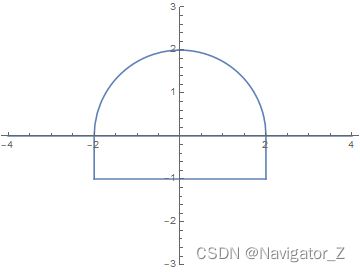
13. 求 由 抛 物 线 y = x 2 及 直 线 y = 1 所 围 成 的 均 匀 薄 片 ( 面 密 度 为 常 数 μ ) 对 于 直 线 y = − 1 的 转 动 惯 量 . \begin{aligned}&13. \ 求由抛物线y=x^2及直线y=1所围成的均匀薄片(面密度为常数\mu)对于直线y=-1的转动惯量.&\end{aligned} 13. 求由抛物线y=x2及直线y=1所围成的均匀薄片(面密度为常数μ)对于直线y=−1的转动惯量.
解:
闭 区 域 D = { ( x , y ) ∣ − y ≤ x ≤ y , 0 ≤ y ≤ 1 } , 所 求 转 动 惯 量 为 I = ∬ D μ ( y + 1 ) 2 d σ = μ ∫ 0 1 ( y + 1 ) 2 d y ∫ − y y d x = 2 μ ∫ 0 1 y ( y + 1 ) 2 d y = 2 μ ∫ 0 1 ( y 5 2 + 2 y 3 2 + y 1 2 ) d y = 368 105 μ . \begin{aligned} &\ \ 闭区域D=\{(x, \ y)\ |\ -\sqrt{y} \le x \le \sqrt{y},0 \le y \le 1\},所求转动惯量为I=\iint_{D}\mu(y+1)^2d\sigma=\\\\ &\ \ \mu \int_{0}^{1}(y+1)^2dy\int_{-\sqrt{y}}^{\sqrt{y}}dx=2\mu \int_{0}^{1}\sqrt{y}(y+1)^2dy=2\mu \int_{0}^{1}(y^{\frac{5}{2}}+2y^{\frac{3}{2}}+y^{\frac{1}{2}})dy=\frac{368}{105}\mu. & \end{aligned} 闭区域D={(x, y) ∣ −y≤x≤y,0≤y≤1},所求转动惯量为I=∬Dμ(y+1)2dσ= μ∫01(y+1)2dy∫−yydx=2μ∫01y(y+1)2dy=2μ∫01(y25+2y23+y21)dy=105368μ.
14. 设 在 x O y 面 上 有 一 质 量 为 M 的 质 量 均 匀 的 半 圆 形 薄 片 , 占 有 平 面 闭 区 域 D = { ( x , y ) ∣ x 2 + y 2 ≤ R 2 , y ≥ 0 } , 过 圆 心 O 垂 直 于 薄 片 的 直 线 上 有 一 质 量 为 m 的 质 点 P , O P = a , 求 半 圆 形 薄 片 对 质 点 P 的 引 力 . \begin{aligned}&14. \ 设在xOy面上有一质量为M的质量均匀的半圆形薄片,占有平面闭区域\\\\&\ \ \ \ \ \ D=\{(x, \ y)\ |\ x^2+y^2 \le R^2,y \ge 0\},过圆心O垂直于薄片的直线上有一质量为m的质点P,OP=a,\\\\&\ \ \ \ \ \ 求半圆形薄片对质点P的引力.&\end{aligned} 14. 设在xOy面上有一质量为M的质量均匀的半圆形薄片,占有平面闭区域 D={(x, y) ∣ x2+y2≤R2,y≥0},过圆心O垂直于薄片的直线上有一质量为m的质点P,OP=a, 求半圆形薄片对质点P的引力.
解:
积 分 区 域 D = { ( ρ , θ ) ∣ 0 ≤ ρ ≤ R , 0 ≤ θ ≤ π } , 因 为 D 关 于 y 轴 对 称 , 且 质 量 分 布 均 匀 , 所 以 F x = 0 , 又 因 薄 片 的 面 密 度 μ = M 1 2 π R 2 = 2 M π R 2 , 则 F y = G m μ ∬ D y ( x 2 + y 2 + a 2 ) 3 2 d σ 极 坐 标 ‾ ‾ G m μ ∫ 0 π d θ ∫ 0 R ρ s i n θ ( ρ 2 + a 2 ) 3 2 ⋅ ρ d ρ = 2 G m μ ∫ 0 R ρ 2 ( ρ 2 + a 2 ) 3 2 d ρ = 4 G m M π R 2 ( l n R 2 + a 2 + R a − R R 2 + a 2 ) , F z = − G a m μ ∬ D d σ ( x 2 + y 2 + a 2 ) 3 2 = − G a m μ ∫ 0 π d θ ∫ 0 R ρ ( ρ 2 + a 2 ) 3 2 d ρ = − 2 G a m M R 2 ( 1 a − 1 R 2 + a 2 ) = − 2 G m M R 2 ( 1 − a R 2 + a 2 ) , 所 求 引 力 为 F = ( 0 , F y , F z ) . \begin{aligned} &\ \ 积分区域D=\{(\rho, \ \theta)\ |\ 0 \le \rho \le R,0 \le \theta \le \pi\},因为D关于y轴对称,且质量分布均匀,所以F_x=0,\\\\ &\ \ 又因薄片的面密度\mu=\frac{M}{\frac{1}{2}\pi R^2}=\frac{2M}{\pi R^2},则\\\\ &\ \ F_y=Gm\mu \iint_{D}\frac{y}{(x^2+y^2+a^2)^{\frac{3}{2}}}d\sigma \underline{\underline{极坐标}}Gm\mu \int_{0}^{\pi}d\theta \int_{0}^{R}\frac{\rho sin\ \theta}{(\rho^2+a^2)^{\frac{3}{2}}}\cdot \rho d\rho=\\\\ &\ \ 2Gm\mu \int_{0}^{R}\frac{\rho^2}{(\rho^2+a^2)^{\frac{3}{2}}}d\rho=\frac{4GmM}{\pi R^2}\left(ln\ \frac{\sqrt{R^2+a^2}+R}{a}-\frac{R}{\sqrt{R^2+a^2}}\right),\\\\ &\ \ F_z=-Gam\mu \iint_{D}\frac{d\sigma}{(x^2+y^2+a^2)^{\frac{3}{2}}}=-Gam\mu \int_{0}^{\pi}d\theta \int_{0}^{R}\frac{\rho}{(\rho^2+a^2)^{\frac{3}{2}}}d\rho=-\frac{2GamM}{R^2}\left(\frac{1}{a}-\frac{1}{\sqrt{R^2+a^2}}\right)=\\\\ &\ \ -\frac{2GmM}{R^2}\left(1-\frac{a}{\sqrt{R^2+a^2}}\right),所求引力为F=(0, \ F_y, \ F_z). & \end{aligned} 积分区域D={(ρ, θ) ∣ 0≤ρ≤R,0≤θ≤π},因为D关于y轴对称,且质量分布均匀,所以Fx=0, 又因薄片的面密度μ=21πR2M=πR22M,则 Fy=Gmμ∬D(x2+y2+a2)23ydσ极坐标Gmμ∫0πdθ∫0R(ρ2+a2)23ρsin θ⋅ρdρ= 2Gmμ∫0R(ρ2+a2)23ρ2dρ=πR24GmM(ln aR2+a2+R−R2+a2R), Fz=−Gamμ∬D(x2+y2+a2)23dσ=−Gamμ∫0πdθ∫0R(ρ2+a2)23ρdρ=−R22GamM(a1−R2+a21)= −R22GmM(1−R2+a2a),所求引力为F=(0, Fy, Fz).
15. 求 质 量 分 布 均 匀 的 半 个 旋 转 椭 球 体 Ω = { ( x , y , z ) ∣ x 2 + y 2 a 2 + z 2 b 2 ≤ 1 , z ≥ 0 } 的 质 心 . \begin{aligned}&15. \ 求质量分布均匀的半个旋转椭球体\Omega=\left\{(x, \ y, \ z)\ |\ \frac{x^2+y^2}{a^2}+\frac{z^2}{b^2} \le 1,z \ge 0\right\}的质心.&\end{aligned} 15. 求质量分布均匀的半个旋转椭球体Ω={(x, y, z) ∣ a2x2+y2+b2z2≤1,z≥0}的质心.
解:
设 质 心 为 ( x ‾ , y ‾ , z ‾ ) , 根 据 对 称 性 可 知 质 心 位 于 z 轴 上 , 即 x ‾ = y ‾ = 0 , 因 D z = { ( x , y ) ∣ x 2 + y 2 ≤ a 2 ( 1 − z 2 b 2 ) } , ∭ Ω z d v = ∫ 0 b z d z ∬ D z d x d y = ∫ 0 b π a 2 ( 1 − z 2 b 2 ) z d z = π a 2 ∫ 0 b ( z − z 3 b 2 ) d z = π a 2 b 2 4 , V = 1 2 ⋅ 4 3 π a 2 b = 2 π a 2 b 3 , 因 此 z ‾ = π a 2 b 2 4 2 π a 2 b 3 = 3 b 8 , 质 心 为 ( 0 , 0 , 3 b 8 ) . \begin{aligned} &\ \ 设质心为(\overline{x}, \ \overline{y}, \ \overline{z}),根据对称性可知质心位于z轴上,即\overline{x}=\overline{y}=0,因D_z=\left\{(x, \ y)\ \bigg|\ x^2+y^2 \le a^2\left(1-\frac{z^2}{b^2}\right)\right\},\\\\ &\ \ \iiint_{\Omega}zdv=\int_{0}^{b}zdz\iint_{D_z}dxdy=\int_{0}^{b}\pi a^2\left(1-\frac{z^2}{b^2}\right)zdz=\pi a^2\int_{0}^{b}\left(z-\frac{z^3}{b^2}\right)dz=\frac{\pi a^2b^2}{4},V=\frac{1}{2}\cdot \frac{4}{3}\pi a^2b=\frac{2\pi a^2b}{3},\\\\ &\ \ 因此\overline{z}=\frac{\frac{\pi a^2b^2}{4}}{\frac{2\pi a^2b}{3}}=\frac{3b}{8},质心为\left(0, \ 0, \ \frac{3b}{8}\right). & \end{aligned} 设质心为(x, y, z),根据对称性可知质心位于z轴上,即x=y=0,因Dz={(x, y) ∣∣∣∣ x2+y2≤a2(1−b2z2)}, ∭Ωzdv=∫0bzdz∬Dzdxdy=∫0bπa2(1−b2z2)zdz=πa2∫0b(z−b2z3)dz=4πa2b2,V=21⋅34πa2b=32πa2b, 因此z=32πa2b4πa2b2=83b,质心为(0, 0, 83b).
16. 一 球 形 行 星 的 半 径 为 R , 其 质 量 为 M , 其 密 度 呈 球 对 称 分 布 , 并 向 着 球 心 线 性 增 加 , 若 行 星 表 面 的 密 度 为 零 , 则 行 星 中 心 的 密 度 是 多 少 ? \begin{aligned}&16. \ 一球形行星的半径为R,其质量为M,其密度呈球对称分布,并向着球心线性增加,若行星\\\\&\ \ \ \ \ \ 表面的密度为零,则行星中心的密度是多少?&\end{aligned} 16. 一球形行星的半径为R,其质量为M,其密度呈球对称分布,并向着球心线性增加,若行星 表面的密度为零,则行星中心的密度是多少?
解:
设 行 星 中 心 的 密 度 为 μ 0 , 根 据 题 意 , 在 据 球 心 r ( 0 ≤ r ≤ R ) 处 的 密 度 为 μ ( r ) = μ 0 − k r , 由 于 μ ( R ) = μ 0 − k R = 0 , 所 以 k = μ 0 R , 即 μ ( r ) = μ 0 ( 1 − r R ) , 则 M = ∭ r ≤ R μ 0 ( 1 − r R ) r 2 s i n φ d r d φ d θ = μ 0 ∫ 0 2 π d θ ∫ 0 π s i n φ d φ ∫ 0 R ( 1 − r R ) r 2 d r = 4 π μ 0 ∫ 0 R ( 1 − r R ) r 2 d r = μ 0 π R 3 3 , 得 μ 0 = 3 M π R 3 . \begin{aligned} &\ \ 设行星中心的密度为\mu_0,根据题意,在据球心r(0 \le r \le R)处的密度为\mu(r)=\mu_0-kr,由于\mu(R)=\mu_0-kR=0,\\\\ &\ \ 所以k=\frac{\mu_0}{R},即\mu(r)=\mu_0\left(1-\frac{r}{R}\right),则M=\iiint_{r \le R}\mu_0 \left(1-\frac{r}{R}\right)r^2sin\ \varphi drd\varphi d\theta=\\\\ &\ \ \mu_0\int_{0}^{2\pi}d\theta \int_{0}^{\pi}sin\ \varphi d\varphi \int_{0}^{R}\left(1-\frac{r}{R}\right)r^2dr=4\pi \mu_0\int_{0}^{R}\left(1-\frac{r}{R}\right)r^2dr=\frac{\mu_0\pi R^3}{3},得\mu_0=\frac{3M}{\pi R^3}. & \end{aligned} 设行星中心的密度为μ0,根据题意,在据球心r(0≤r≤R)处的密度为μ(r)=μ0−kr,由于μ(R)=μ0−kR=0, 所以k=Rμ0,即μ(r)=μ0(1−Rr),则M=∭r≤Rμ0(1−Rr)r2sin φdrdφdθ= μ0∫02πdθ∫0πsin φdφ∫0R(1−Rr)r2dr=4πμ0∫0R(1−Rr)r2dr=3μ0πR3,得μ0=πR33M.