基于朴素贝叶斯分类器的西瓜数据集（实战）

最近刚开始学习机器学习中的朴素贝叶斯分类器，用西瓜数据集做了一下，最后结果预测正确率75%，其中运用到的python语法并不复杂，适合小白观看。

朴素贝叶斯分类器思想的自然语言描述：

朴素贝叶斯分类器其实就是计算先验概率和每一个属性的条件概率，作乘积并比较，哪个大就是哪一类的，其中对离散属性做拉普拉斯修正，连续属性用概率密度函数。

 

因此要保存每一个属性的每一个取值在每一个分类中的条件概率，比如色泽是青绿在好瓜中的条件概率。由于属性个数很多每一个属性的取值也有很多，因此要考虑冗杂的数据如何保存，这点清楚了预测时直接乘就行。我们可以用字典数组来保存离散属性的先验概率和条件概率（或连续属性的均值和方差）。

给定表1中的训练数据，编程实现贝叶斯分类器算法，并为表2中测试数据进行分类；

表1：训练集

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.46	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	0.774	0.376	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	0.634	0.264	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	0.608	0.318	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	0.556	0.215	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	0.403	0.237	是
7	浅白	硬挺	清脆	模糊	平坦	硬滑	0.245	0.057	否
8	浅白	蜷缩	浊响	模糊	平坦	软粘	0.343	0.099	否
9	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	0.639	0.161	否
10	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	0.657	0.198	否
11	乌黑	稍蜷	浊响	清晰	稍凹	软粘	0.36	0.37	否
12	浅白	蜷缩	浊响	模糊	平坦	硬滑	0.593	0.042	否
13	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	0.719	0.103	否

表2：测试集

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
1	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	0.481	0.149	是
2	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	0.437	0.211	是
3	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	0.666	0.091	否
4	青绿	硬挺	清脆	清晰	平坦	软粘	0.243	0.267	否

详细步骤在代码中说明

import pandas as pd
import numpy as np


# 将数据集分别保存在excel表中的不同工作表中，用pandas导入，其余都用numpy来做
def load_data():
    # 导入数据
    train_data = pd.read_excel('data.xlsx', sheet_name='train')
    test_data = pd.read_excel('data.xlsx', sheet_name='test')
    # ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率', '好瓜‘]
    train_data = np.array(train_data)[:, 1:]
    test_data = np.array(test_data)[:, 1:]
    return train_data, test_data


# 训练贝叶斯分类器，其实就是计算离散属性的先验概率和条件概率、连续属性的均值和方差
def train_bayes(train_data):  # 13行9列
    # 先计算先验概率P(c)，即好瓜和坏瓜的个数分别占总训练集样本个数的比例
    good_num = 0
    bad_num = 0  # 好瓜与坏瓜的个数，后面拉普拉斯修正也要用
    for i in range(train_data.shape[0]):  # 一行一行地看，shape[0]指行数
        if train_data[i, -1] == "是":
            good_num += 1
        elif train_data[i, -1] == "否":
            bad_num += 1
    # 得到好瓜6个，坏瓜7个
    # 计算先验概率
    pc_good = (good_num + 1) / (train_data.shape[0] + 2)  # 公式见西瓜书p153
    pc_bad = (bad_num + 1) / (train_data.shape[0] + 2)

    # 将分类结果的好瓜与坏瓜分开,典的第一个键值对保存该属性的取值个数,例如本训练集中色泽有三种取值(青绿,乌黑,浅白),就保存
    # 保存每一个属性的取值个数是为了进行拉普拉斯修正
    good_melon = [{'sumType': 0} for i in range(8)]
    bad_melon = [{'sumType': 0} for i in range(8)]

    # 计算条件概率P(xi | c)，例如计算在好瓜中色泽为青绿的个数占好瓜总数的比例
    for j in range(train_data.shape[1] - 3):  # 一列一列地看，shape[1]指列数,最后三列不看
        # 一行一行地看，这两行正反都一样
        for i in range(train_data.shape[0]):
            # 首先保证是好瓜
            if train_data[i, -1] == "是":
                # 如果字典数组中已经有了这个属性对应的值（如青绿）就直接加一
                if train_data[i, j] in good_melon[j]:
                    good_melon[j][train_data[i, j]] += 1
                else:
                    good_melon[j][train_data[i, j]] = 1  # 如果没有就创建一个键值对并赋值为1
                    good_melon[j]['sumType'] += 1  # 该属性增加一个取值

            else:  # 如果是坏瓜，把上面good_melon换成bad_melon就行
                if train_data[i, j] in bad_melon[j]:  # 如果字典数组中已经有了这个属性对应的值（如青绿）就直接加一
                    bad_melon[j][train_data[i, j]] += 1
                else:
                    bad_melon[j][train_data[i, j]] = 1  # 如果没有就创建一个键值对并赋值为1
                    bad_melon[j]['sumType'] += 1  # 该属性增加一个取值

    # 因为拉普拉斯修正中每一个属性的取值是整个训练集的取值，上面只是单独收集好瓜与坏瓜
    for i in range(len(good_melon) - 2):
        # if或者elif成立说明有属性只在好瓜和坏瓜中存在，要统一一下
        if good_melon[i]['sumType'] > bad_melon[i]['sumType']:
            # 统一属性取值个数
            bad_melon[i]['sumType'] = good_melon[i]['sumType']
            # 统一取值
            key = good_melon[i].keys() - bad_melon[i].keys()
            bad_melon[i][key] = 0
            print(bad_melon[i][key])
        elif good_melon[i]['sumType'] < bad_melon[i]['sumType']:
            # 统一属性取值个数
            good_melon[i]['sumType'] = bad_melon[i]['sumType']
            # 统一取值
            key = list(bad_melon[i].keys() - good_melon[i].keys())
            for j in key:
                good_melon[i][j] = 0

    # 上面只是统计了个数，下面才是计算条件概率，直接用统计出来的数值除以好瓜或者坏瓜的个数
    for i in range(train_data.shape[1] - 3):  # 有train_data.shape[0] - 3个是离散属性，需要进行拉普拉斯修正
        for key, value in good_melon[i].items():  # 遍历每一个键值对，好瓜
            if key != "sumType":  # 除了字典的第一个值
                good_melon[i][key] = (good_melon[i][key] + 1) / (good_num + good_melon[i]['sumType'])
        for key, value in good_melon[i].items():  # 遍历每一个键值对，坏瓜
            if key != "sumType":  # 除了字典的第一个值
                bad_melon[i][key] = (bad_melon[i][key] + 1) / (bad_num + bad_melon[i]['sumType'])

    # 以上是离散属性的先验概率和条件概率
    # 下面是连续属性的均值和方差 -1是含糖率，-2是密度
    good_melon[-1]['mean'] = np.mean(train_data[:6, -2], axis=0)
    good_melon[-1]['var'] = np.var(train_data[:6, -2], axis=0)
    bad_melon[-1]['mean'] = np.mean(train_data[6:, -2], axis=0)
    bad_melon[-1]['var'] = np.var(train_data[6:, -2], axis=0)

    good_melon[-2]['mean'] = np.mean(train_data[:6, -3], axis=0)
    good_melon[-2]['var'] = np.var(train_data[:6, -3], axis=0)
    bad_melon[-2]['mean'] = np.mean(train_data[6:, -3], axis=0)
    bad_melon[-2]['var'] = np.var(train_data[6:, -3], axis=0)

    # print(f'好瓜 {good_melon}')
    # print(f'坏瓜 {bad_melon}')
    # 结果如下： 好瓜[{'sumType': 3, '青绿': 0.4444444444444444, '乌黑': 0.3333333333333333, '浅白': 0.2222222222222222},
    # { 'sumType': 3, '蜷缩': 0.6666666666666666, '稍蜷': 0.2222222222222222, '硬挺': 0.1111111111111111}, { 'sumType': 3,
    # '浊响': 0.5555555555555556, '沉闷': 0.3333333333333333, '清脆': 0.1111111111111111}, { 'sumType': 3,
    # '清晰': 0.7777777777777778, '模糊': 0.1111111111111111, '稍糊': 0.1111111111111111}, { 'sumType': 3,
    # '凹陷': 0.6666666666666666, '稍凹': 0.2222222222222222, '平坦': 0.1111111111111111}, { 'sumType': 2, '硬滑': 0.75,
    # '软粘': 0.25}, {'sumType': 0, 'means': 0.612, 'var': 0.01346433333333333}, { 'sumType': 0,
    # 'means': 0.3116666666666667, 'var': 0.0072288888888888915}] 坏瓜[{'sumType': 3, '浅白': 0.5, '青绿': 0.3, '乌黑': 0.2},
    # {'sumType': 3, '硬挺': 0.2, '蜷缩': 0.4, '稍蜷': 0.4}, { 'sumType': 3, '清脆': 0.2, '浊响': 0.5, '沉闷': 0.3}, {'sumType':
    # 3, '模糊': 0.4, '稍糊': 0.4, '清晰': 0.2}, { 'sumType': 3, '平坦': 0.4, '凹陷': 0.3, '稍凹': 0.3}, {'sumType': 2,
    # '硬滑': 0.6666666666666666, '软粘': 0.3333333333333333}, {'sumType': 0, 'mean': 0.508,
    # 'var': 0.029915142857142855}, { 'sumType': 0, 'mean': 0.14714285714285716, 'var': 0.010841551020408164}]

    return pc_good,pc_bad,good_melon, bad_melon


# 开始对测试集分类
def classify_bayes(pc_good,pc_bad,good_melon, bad_melon, test_data):
    # 对每一个测试数据进行计算好瓜与坏瓜的概率
    for i in range(test_data.shape[0]):
        # 每一个测试数据都要先令其等于先验概率的对数，后面全部取对数直接相加
        good_probability = np.log(pc_good)
        bad_probability = np.log(pc_bad)
        for j in range(test_data.shape[1] - 3):  # 先处理离散属性
            if test_data[i][j] in good_melon[j]:  # 如果这个特征训练集没有就跳过
                good_probability += np.log(good_melon[j][test_data[i][j]])  # 转化为对数相加
            if test_data[i][j] in bad_melon[j]:
                bad_probability += np.log(bad_melon[j][test_data[i][j]])
        for j in range(test_data.shape[1] - 3, test_data.shape[1] - 1):  # 处理连续属性
            good_probability += np.log((2 * np.pi * good_melon[j]['var']) ** (-1 / 2)) + \
                                (-1 / 2) * ((test_data[i][j] - good_melon[j]['mean']) ** 2) / (
                                            good_melon[j]['var'] ** (-2))
            bad_probability += np.log((2 * np.pi * bad_melon[j]['var']) ** (-1 / 2)) + \
                               (-1 / 2) * ((test_data[i][j] - bad_melon[j]['mean']) ** 2) / (
                                       bad_melon[j]['var'] ** (-2))
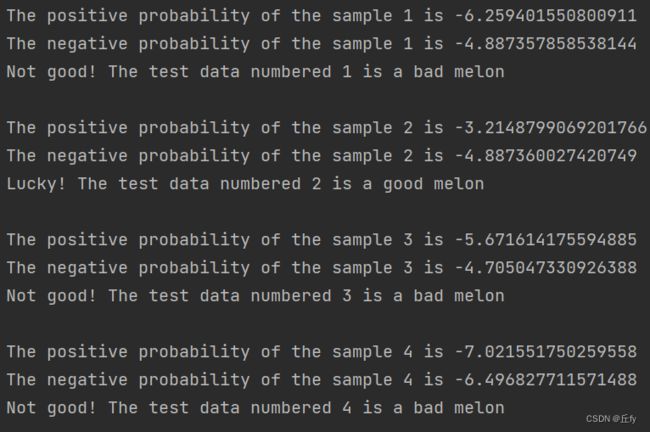
        print(f'The positive probability of the sample {i + 1} is {good_probability}\n\
The negative probability of the sample {i + 1} is {bad_probability}')
        if good_probability > bad_probability:
            print(f'Lucky! The test data numbered {i + 1} is a good melon\n')
        else:
            print(f'Not good! The test data numbered {i + 1} is a bad melon\n')


if __name__ == "__main__":
    train_data, test_data = load_data()
    pc_good,pc_bad,good_melon, bad_melon = train_bayes(train_data)
    classify_bayes(pc_good,pc_bad,good_melon, bad_melon, test_data)

运行结果：