聚类分析实验——机器学习
文章目录
- 一、实验要求
- 二、实验目的
- 三、实验内容
-
- 实验步骤
-
- 1.请根据cluster文件代码,根据K均值聚类算法的原理,有两种初始化方法,一种是随机中心点,一种是随即分类,请修改代码实现另一种初始化也就是随机分类代码,然后观察聚类过程比较两种随机初始化方法效果。
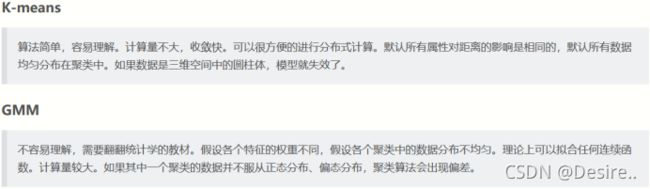
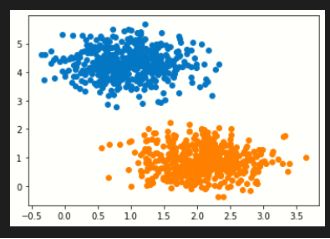
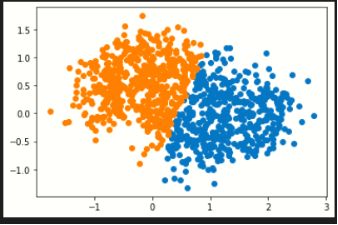
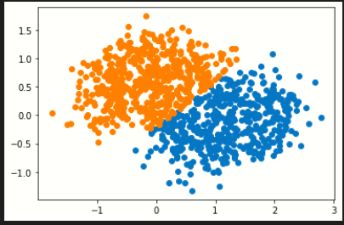
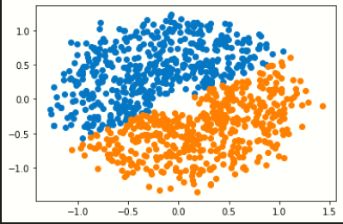
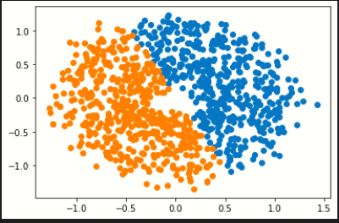
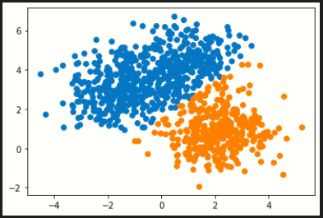
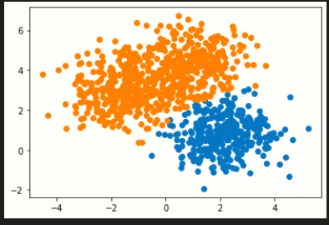
- 2.请对比sklearn的K均值聚类和混合高斯模型,针对make_blobs生成的基本数据集, makemoons生成的太极数据集,makecircles生成的圆环数据集,多类数据集,对比聚类的效果如何。
一、实验要求
在计算机上验证和测试k-means聚类和高斯混合模型聚类实验,sklearn的相关聚类算法。
二、实验目的
1、掌握k-means聚类算法的原理
2、掌握高斯混合模型聚类算法的原理;
3、掌握sklearn如何实现聚类;
三、实验内容
实验步骤
1.请根据cluster文件代码,根据K均值聚类算法的原理,有两种初始化方法,一种是随机中心点,一种是随即分类,请修改代码实现另一种初始化也就是随机分类代码,然后观察聚类过程比较两种随机初始化方法效果。
随机中心点与随机分类:
#聚类算法
import numpy as np
class KMeans:
def __init__(self,n_clusters=5,max_iter=15):
self._n_clusters=n_clusters
self._X=None
self._y=None
self._center = None
self._max_iter=max_iter
#随机中心点初始化
def fit(self,X):
self._X=X
n=X.shape[0]
d=X.shape[1]
#随机生成中心点
self._center = np.array([[np.random.uniform(mi,mx) for mi,mx in zip(X.min(axis=0),X.max(axis=0))] for _ in range(self._n_clusters)])
step=0
#迭代
while step < self._max_iter:
#求样本点与每个中心点的距离
distances = np.array([np.sum((X-self._center[i,:])**2,axis=1) for i in range(self._n_clusters)])
#样本距离哪个最近中心点
self._y = np.argmin(distances.T,axis=1)
#对样本点加权平均计算新的中心点
self._center = np.array([np.mean(X[self._y==i,:],axis=0) for i in range(self._n_clusters)])
step+=1
#显示中间过程
plt.figure()
plt.scatter(X[self._y==0,0],X[self._y==0,1],marker='+')
plt.scatter(X[self._y==1,0],X[self._y==1,1],marker='+')
plt.scatter(X[self._y==2,0],X[self._y==2,1],marker='+')
plt.scatter(self._center[0,0],self._center[0,1])
plt.scatter(self._center[1,0],self._center[1,1])
plt.scatter(self._center[2,0],self._center[2,1])
plt.show()
return self
#随机分类初始化
def fit1(self,X):
self._X=X
n=X.shape[0]
d=X.shape[1]
self._y =np.random.permutation(np.array([0,1,2]*50))
#根据随机分类生成初始中心点
self._center = np.array([np.mean(X[self._y==i,:],axis=0) for i in range(self._n_clusters)])
step=0
#迭代
while step < self._max_iter:
#求样本点与每个中心点的距离
distances = np.array([np.sum((X-self._center[i,:])**2,axis=1) for i in range(self._n_clusters)])
#样本距离哪个最近中心点
self._y = np.argmin(distances.T,axis=1)
#对样本点加权平均计算新的中心点
self._center = np.array([np.mean(X[self._y==i,:],axis=0) for i in range(self._n_clusters)])
step+=1
#显示中间过程
plt.figure()
plt.scatter(X[self._y==0,0],X[self._y==0,1],marker='+')
plt.scatter(X[self._y==1,0],X[self._y==1,1],marker='+')
plt.scatter(X[self._y==2,0],X[self._y==2,1],marker='+')
plt.scatter(self._center[0,0],self._center[0,1])
plt.scatter(self._center[1,0],self._center[1,1])
plt.scatter(self._center[2,0],self._center[2,1])
plt.show()
return self
结果图显示:
#聚类算法
from sklearn import datasets
import matplotlib.pyplot as plt
iris = datasets.load_iris()
X=iris.data[:,2:]
km1=KMeans(n_clusters=3)
km1.fit(X) #fit为随机中心点初始化,fit1为随机分类初始化
比较:
k-means聚类算法的初 始点选择不稳定,是随机选取的,这就引起聚类结果的不稳定,本实验中虽是经过多次实验取的平均值,但是具体初始点的选择方法还需进一步研究;层次聚类虽然 不需要确定分类数,但是一旦一个分裂或者合并被执行,就不能修正,聚类质量受限制。