DANet：Dual Attention Network for Scene Segmentation论文解读和源代码详解
今天为大家带来一篇CVPR2019的语义分割的一篇文章，我认为也是非常新颖的了。其中的对偶结构生成的attention map我认为很容易嵌入到其他网络中完成其他任务。
论文地址：here
官方源码：(基于pytorch)[https://github.com/junfu1115/DANet]
提出背景
当前的主流的语义分割网络应该就是空洞卷积和解码器这两个元素的组合。但这两个组件都是利用局部特征（因为卷积操作就是稀疏连接嘛，一次卷积能覆盖特征图全部的信息吗？当然不行啦，所以说是利用局部特征），作者提出两种模块，分别从分辨率维度（spatial）和通道维度来引入全局的信息，将局部特征和全局的依赖性自适应地整合到一起。
之前的一些方法，往往有两个问题。第一个是，如果某些目标受到光照，遮挡等因素不够显著，那么这些位置的预测结果很可能就被一些显著性的物体所影响了。第二个问题是，一张图像中很多物体的尺度是不一样的，占比不一样，那么不同尺度的特征应该被同等对待。作者通过自注意力机制从全局视野自适应地在整合任何尺度的相似的特征（没有明白的话，看下面的attention map的可视化应该就可以明白了）。作者认为局部特征对应的全局性的依赖是很重要的。
主要贡献
- 提出了一种新颖的对偶注意力网络，利用自注意力机制提高特征表示的判别性。
- 位置注意力模块用于学习特征的空间依赖性，通道注意力模块用来学习通道之间的内部关联性。
- 在cityscapes，PASCAL context，COCO stuff上实现了更好的性能
方法
如果给结构分类，我会把它分到空洞卷积那类中，因为没有解码器嘛。
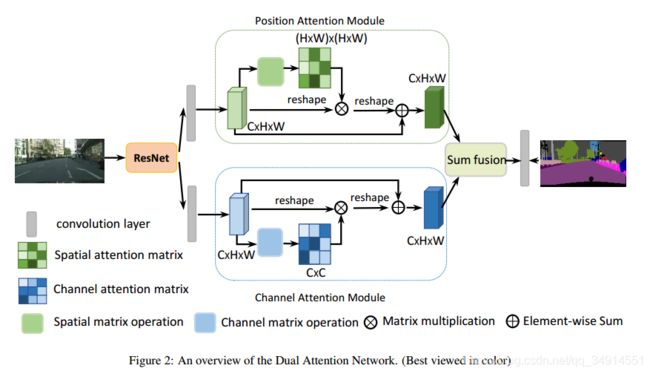
backbone是ResNet，50或者101，都行，重点是融合空洞卷积核并删除了池化层的ResNet，其实就是现在流行的deeplab中使用的resnet结构了，注意resnet输出的特征图是原始尺寸的 1 8 \frac{1}{8} 81倍。
之后分两路（当然这里的resnet是只用卷积层部分，去除全连接层的！），这两路都先进过一个卷积层，然后分别送到位置注意力模块和通道注意力模块中去。这两个模块就有点意思了。理解起来比较费力气的。
先看下位置注意力模块的具体结构。
位置注意力模块 PAM
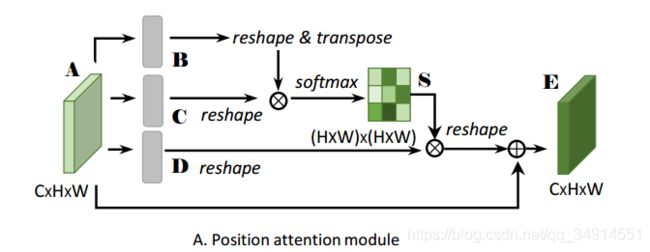
A就是模块的输入，它被分别送到三个卷积层中获得了B，C，D。这四个特征图都是一样大小的，都是 R C × H × W 的 R^{C\times H\times W}的 RC×H×W的。现在把B和C都reshape为 R C × N R^{C \times N} RC×N，其中 N = H × W N= H\times W N=H×W 。 然后将C的转置和B相乘，得到了 S ∈ R N × N S \in R^{N \times N} S∈RN×N，然后按行(axis=1)做softmax运算。见原文
s j i s_{ji} sji就是第j行第i列的元素，它等于 B B B的第i列乘上 C C C的第J列的指数除以下面那串玩意，如果你耐心推导，就是把得到的S按列（axis = -1， 对于channel first形式）求softmax运算，再赋值给S。 s j i s_{ji} sji代表着第i个位置的特征对第J个位置的影响，如果这两个位置恰好都是属于同一类的像素点，那么 s j i s_{ji} sji就会产生很大的值，这样就会突出相似特征之间的联系，但其实为啥能这样我没看懂。再说一下， B i , B j B_i,B_j Bi,Bj其实都是 R 1 × C R^{1\times C} R1×C的，i和j都是遍历 1 , 2 , . . . , H × W 1,2,...,H\times W 1,2,...,H×W的，其实是空间维度上的运算，空间维度上的一个像素点的特征不就是 R 1 × C R^{1\times C} R1×C的嘛！
那么 s j i s_{ji} sji确实能有表示第i个位置的特征对第J个位置的影响的意义，不过我也确实不明白为啥这样运算就是一个位置对另一个位置的影响。
Update on 2019.9.16
评论中一些人问我，为什么仅仅通过矩阵相乘，就可以建模像素和全局的联系。其实这个问题也是蛮容易想到的，它不是由来以及。在人脸识别领域，常常用余弦距离，如果两个向量的夹角很小，则说明这两个向量很相似。我们熟知的图像分类网络，最后有一个FC层，目的是做矩阵的乘法，如果对应位置得到一个很大的值，说明属于这一类的概率很高，矩阵相乘本质也是向量相乘。
那么对于自注意力。如果大家仔细阅读，会发现相乘的这两个矩阵本身reshape的方式不一样。他们之间的矩阵相乘，内部其实是一个像素对应的特征向量和其他所有位置的特征向量的乘积。self attention其实是想通过点积（dot）的方式，优化向量的距离，即点积相似性：如果两个向量的乘积越大，姑且可以认为这两个向量在特征空间的分布距离很近，则它们很相似。以此来建模像素之间的联系。
然后把Dreshape为 R C × N R^{C\times N} RC×N，再做下面的运算
D i D_i Di是 D D D的第 i i i列。a是训练参数，也是自注意力参数，等下说。按上面的公式，J遍历到 1 , 2 , . . . , C 1,2,...,C 1,2,...,C就得到了 E ∈ R C × N E \in R^{C\times N} E∈RC×N即 R C × H × W R^{C\times H \times W} RC×H×W。之后这个特征图在经过一个卷积层，论文中没写（源码中写了），作为这个模块的输出。
通道注意力模块 CAM
和PAM很类似，只不过这里的向量全部都是 R 1 × N R^{1\times N} R1×N的了。
而且整个模块是没有卷积层的。也是有个自注意力参数
过程我不重复了哈。很相似的。
自注意力参数
为啥叫自注意力呢，如果这两个参数为0，我们会发现两个模块其实没起到作用的。OK，我相信有人已经懂了，这两个参数确实用0初始化，随着参数更新，网络如果觉得模块有用，自然会增加这两个参数的值。即残差思想，最差我就不用这个模块了，最好就是将参数更新到合适的位置，自己去寻找最优的利用度。
实验
乱起八早的实验设置我跳过了，和大部分的语义分割网络是一致的，我也不想随意贴几张实验结果图看看指标敷衍了事。我们直接看看我认为最有意思的部分。
因为 S ∈ R N × N S\in R^{N\times N} S∈RN×N，那么 S S S可以被视为是 R ( H × W ) × ( H × W ) R^{(H\times W)\times (H\times W)} R(H×W)×(H×W)的，每一个像素点位置都对应有一个 H × W H\times W H×W的子map，作者就抽取这个子map，看看attention map究竟是啥玩意。
第一列的红色点就是作者抽取的点，第二列对应标号为1的点的attention map，第三列对应标号为2的点的attention map。我们发现，attention map可以说将相同label的物体都不同程度显示出来了。越亮的地方表示该点对全局位置上具有相同label的点的依赖关系越强。所以回想起公式
也是显式的用注意力机制放大相似且关联的特征的值。
作者同样抽取了第4和11通道，通过热图看看哪些区域被注意到了，越红的地方表示响应越大，即那些点都是一类的。
以上两方面的观察我们就明白了，两个模块PAM和CAM具有全局性的找寻相似特征的能力，并将他们建立起关系，无论像素点的空间距离是多少。
另外模型有很多矩阵运算，所以运行时间比较长；但该方法的理论我认为很强’
从源码看PAM和CAM
首先定义了三个卷积层，而且softmax的定义是按最后一个维度做运算，其实就是按列嘛。
在forward里面我们也可以看到步骤确实如上面所述。将一个卷积层的输出reshape之后转置，torch.bmm就是不在batch size那个位置做矩阵相乘（按第一个维度分开，分别在对应的batchsize维度做矩阵乘法。）。然后经过softmax，把D也reshape。
注意下面的公式可以换成矩阵相乘的写法。
所以我们才看到
out = torch.bmm(proj_value, attention.permute(0, 2, 1)) # permute 就是转置的意思
out = out.view(m_batchsize, C, height, width)
out = self.gamma*out + x
这三行，就对应上面的公式。 gamma就是自注意力参数，因为是常数，所以提出来最后才乘上去。
CAM 也是一样差不多的。就跳过了。那么既然官方开源了代码，我当然要试试看看啦
实现效果
源码不太好调试，未完待续-
上面的结果是我直接将2048x1024大小的原图resize成512x512的大小的结果，所以图像有不成比例的扭曲。因为内存占用太大了。如果我想获得好的结果，同样可以crop在将patch拼接，我懒就没弄了。但就从上面的结果来看，还是不错的，毕竟用的也是人家做实验的预训练模型。