贝塞尔曲线原理--曲线生成--路径规划--matlab代码

贝塞尔曲线的原理:

从例子入手:

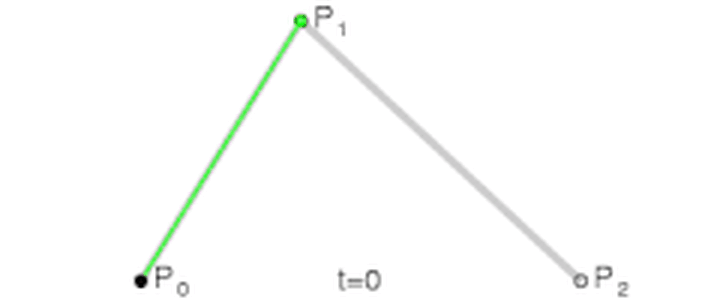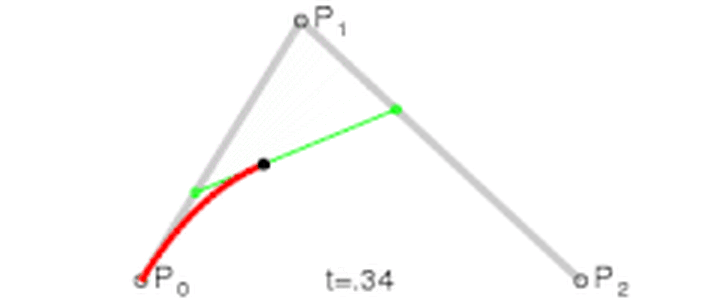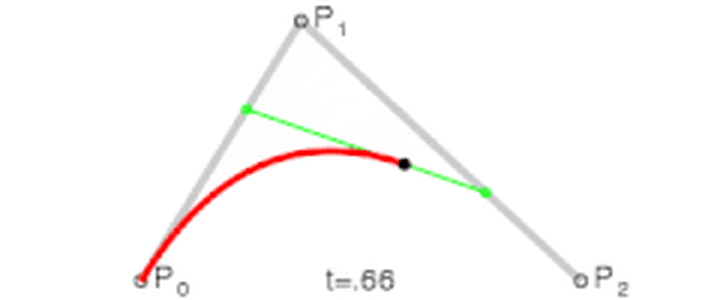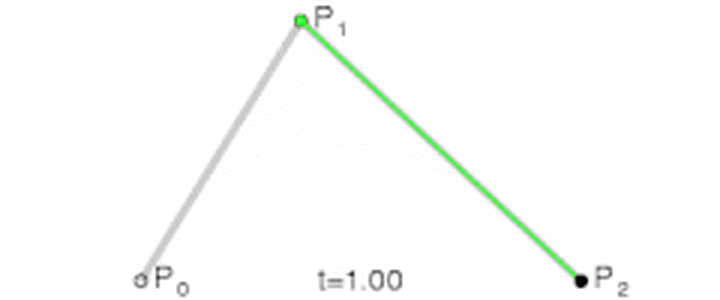
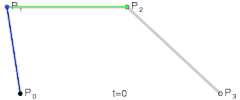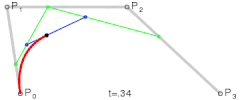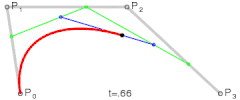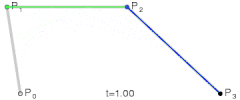
这里的 P0、P1、P2 分别称之为控制点，贝塞尔曲线的产生完全与这三个点位置相关。

这也就意味着，我们可以通过调节控制点的位置，进而调整整个曲线。

贝塞尔曲线是一个对强迫症极其友好的曲线，看这个动图就让人很舒适，而它的构造方法也一样让人很舒适。

最开始，对于绿色线段的两头 Q0 和 Q1，将其分别放在 P0 和 P1 的位置，此时让它们运动，要求：Q0 往 P1 方向，Q1 往 P2 方向，分别匀速运动，并且同时到达线段的另一头。

转化成数学公式，即为

在绿色线段上再取一个点 B ，如果 B 在绿色线段上的运动也满足上述的规律，那岂不是很爽！所以不妨再规定：

 

令上述等式等于 t，t 肯定是 [0,1] 的，其意义是点在它所处线段的位置。那么随着 t 的增大，Q0、Q1、B 的位置也就随之确定了！最终 B 的轨迹，便构成了贝塞尔曲线。

递归性质

仔细观察一下上述的构造过程，我们可以观察到：

首先，有三个控制点；

三个控制点形成两个线段，每个线段上有一个点在运动，于是得到两个点；

两个点形成一个线段，这个线段上有一个点在运动，于是得到一个点；

最后一个点的运动轨迹便构成了贝塞尔曲线！

我们发现，实际上是每轮都是 n 个点，形成 n-1 条线段，每个线段上有一个点在运动，那么就只关注这 n-1 个点，循环往复。最终只剩一个点时，它的轨迹便是结果。

那么，似乎最开始的控制点，也不一定是三个？如果是四个、五个，甚至更多呢？

四个点:

五个点:

 

 如此一来，你会发现贝塞尔曲线内的递归结构。实际上，上述介绍的分别是三阶、四阶、五阶的贝塞尔曲线，贝塞尔曲线可以由阶数递归定义。

知识部分理解可以参考:怎么理解贝塞尔曲线？ - 知乎 (zhihu.com)

或者:从零开始学图形学：10分钟看懂贝塞尔曲线 - 知乎 (zhihu.com)

下面用matlab代码展示贝塞尔曲线形成过程:

基本思路来自于:

 代码:

%% 一、二、三阶贝塞尔曲线生成
%jubobolv
clc;
clear;
close all;
%% 一次贝塞尔曲线
P0=[0,0];
P1=[1,1];
P=[P0;P1];
figure(1);
plot(P(:,1),P(:,2),'k');
MakeGif('一次贝塞尔曲线.gif',1);
hold on

for t=0:0.01:1
    P_t=(1-t) * P0 + t * P1;
    scatter(P_t(1),P_t(2),200,'.r');
    stringName = "一次贝塞尔曲线：t="+num2str(t);
    title(stringName);
    MakeGif('一次贝塞尔曲线.gif',t*100+1);
end

%% 二次贝塞尔曲线
P0=[0,0];
P1=[1,1];
P2=[2,1];
P=[P0;
    P1;
    P2];
figure(2);
plot(P(:,1),P(:,2),'k');
MakeGif('二次贝塞尔曲线.gif',1);
hold on

scatter(P(:,1),P(:,2),200,'.b');
for t=0:0.01:1
    P_t_1=(1-t) * P0 + t * P1;
    P_t_2=(1-t) * P1 + t * P2;
    P_t_3=(1-t) * P_t_1 + t * P_t_2;
    
    m1=scatter(P_t_1(1),P_t_1(2),300,'g');
    m2=scatter(P_t_2(1),P_t_2(2),300,'g');
    
    m3=plot([P_t_1(1),P_t_2(1)],[P_t_1(2),P_t_2(2)],'g','linewidth',2);
    
    scatter(P_t_3(1),P_t_3(2),300,'.r');  
    stringName = "二次贝塞尔曲线：t="+num2str(t);
    title(stringName);
    MakeGif('二次贝塞尔曲线.gif',t*100+1);
    delete(m1);
    delete(m2);
    delete(m3);
end


%% 三次贝塞尔曲线

P0=[0,0];
P1=[1,1];
P2=[2,1];
P3=[3,0];
P=[P0;
    P1;
    P2;
    P3];
figure(3);
plot(P(:,1),P(:,2),'k');
MakeGif('三次贝塞尔曲线.gif',1);
hold on
scatter(P(:,1),P(:,2),200,'.b');

for t=0:0.01:1
    P_t_1=(1-t) * P0 + t * P1;
    P_t_2=(1-t) * P1 + t * P2;
    P_t_3=(1-t) * P2 + t * P3;

    P_t_4=(1-t) * P_t_1 + t * P_t_2;
    P_t_5=(1-t) * P_t_2 + t * P_t_3;
    
    P_t_6=(1-t) * P_t_4 + t * P_t_5;
    
    m1=scatter(P_t_1(1),P_t_1(2),300,'g');
    m2=scatter(P_t_2(1),P_t_2(2),300,'g');
    m3=scatter(P_t_3(1),P_t_3(2),300,'g');
    
    m4=scatter(P_t_4(1),P_t_4(2),300,'m');
    m5=scatter(P_t_5(1),P_t_5(2),300,'m');
    
    m6=plot([P_t_1(1),P_t_2(1),P_t_3(1)],[P_t_1(2),P_t_2(2),P_t_3(2)],'g','linewidth',2);
    m7=plot([P_t_4(1),P_t_5(1)],[P_t_4(2),P_t_5(2)],'m','linewidth',2);
    
    scatter(P_t_6(1),P_t_6(2),300,'.r');  
    
    stringName = "三次贝塞尔曲线：t="+num2str(t);
    title(stringName);
    MakeGif('三次贝塞尔曲线.gif',t*100+1);
    delete(m1);
    delete(m2);
    delete(m3);
    delete(m4);
    delete(m5);
    delete(m6);
    delete(m7);
end

其中调用的生成GIF图的函数MakeGif.m如下：

function [outputArg1,outputArg2] = MakeGif(name,t)
%该函数用于生成动态GIF图
%   参数1：图像名称 参数2：步长（或时间）
    drawnow
    F=getframe(gcf);
    I=frame2im(F);
    [I,map]=rgb2ind(I,256);
    if t == 1
        imwrite(I,map,name,'gif', 'Loopcount',inf,'DelayTime',0.2);
    else
        imwrite(I,map,name,'gif','WriteMode','append','DelayTime',0.2);
    end
    
end

效果图如下：

 

 

 将贝塞尔曲线用于无人车路径规划的障碍物避障

可以尽量使规划路径满足车辆转弯曲率。代码如下：

%% 贝塞尔路径规划
%jubobolv
clc;
clear;
close all;
%% 基本信息 路宽 路长
road_width=3.6;
road_length=40;
%起点 障碍物点 目标点
P0=[2 2];
Pob=[10 2.2;
     18 5.4;
     30 4;];
Pg=[39 5.5];

P=[P0;Pob;Pg];
i=1

%% 贝塞尔曲线计算　基本思路Pt＝(1-t)*P1+t*P2
for t=0:0.01:1
    % 一次贝塞尔曲线
    p_t_1=(1-t)*P(1,:)+t*P(2,:);
    p_t_2=(1-t)*P(2,:)+t*P(3,:);
    p_t_3=(1-t)*P(3,:)+t*P(4,:);
    p_t_4=(1-t)*P(4,:)+t*P(5,:);
    % 二次贝塞尔曲线
    pp_t_1=(1-t)*p_t_1+t*p_t_2;
    pp_t_2=(1-t)*p_t_2+t*p_t_3;
    pp_t_3=(1-t)*p_t_3+t*p_t_4;
    % 三次贝塞尔曲线
    ppp_t_1=(1-t)*pp_t_1+t*pp_t_2;
    ppp_t_2=(1-t)*pp_t_2+t*pp_t_3;
    % 四次贝塞尔曲线
    pppp_t(i,:)=(1-t)*ppp_t_1+t*ppp_t_2;
    i=i+1;
end
%% 作图
figure
% 道路背景填充
fill([0 road_length road_length 0],[0 0 2*road_width 2*road_width],[0.5,0.5,0.5]);

hold on
%车道中间线（两车道中间）
plot([0 road_length],[road_width road_width],'--w','linewidth',2);
%起点
plot(P0(:,1),P0(:,2),'*b');
%障碍物点
plot(Pob(:,1),Pob(:,2),'ob');
%目标点
plot(Pg(:,1),Pg(:,2),'pm');
%绘制贝塞尔规划的路径点
plot(pppp_t(:,1),pppp_t(:,2),'.r');

axis equal
set(gca,'XLim',[0 road_length])
set(gca,'YLim',[0 2*road_width])

效果图如下：